Двухголовочные автоматы

Несмотря на то, что двухленточные и двухголовочные автоматы похожи друг на друга, их свойства сильно отличаются. Так, проблема пустоты разрешима для многоленточных автоматов и неразрешима для многоголовочных.

Более того, в последнем случае она не является даже частично разрешимой. Проблема эквивалентности также не является частично разрешимой для многоголовочных автоматов. Однако проблема эквивалентности разрешима для двухленточных автоматов, и остается пока открытой для многоленточных автоматов с тремя и более лентами.

Двухголовочный конечный автомат (ДКА) имеет одну ленту и две головки, которые могут независимо перемещаться вдоль ленты в одном направлении. Множество состояний Q разбито на два непересекающихся множества. В состояниях Q₁ активна первая головка, а в состояниях Q₂ - вторая.

Двухголовочный автомат можно рассматривать как такой двухленточный автомат, который работает с идентичными словами на обеих лентах.

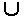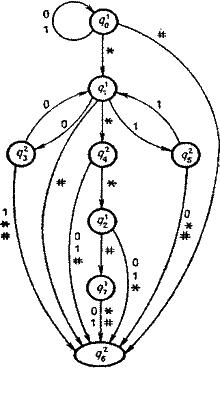
Приведем пример ДКА, который проверяет равенство двух последовательно записанных слов в алфавите V = {0, 1}. Признаком окончания каждого из слов сделаем вспомогательный символ *, не входящий в V. Автомат должен допускать только слова вида а*, а V^*. Пусть A = (V {*}, Q₁ 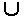Q₂, R, q₀¹, #, I), где Q₁ = {q₀¹, q₁¹, q₂¹, q₇¹} - множество состояний, в которых активна первая головка; Q₂ = {q₃², q₄², q₅², q₆²} - множество состояний, в которых активна вторая головка; R = {q₇¹} - множество, содержащее единственное заключительное состояние. Граф автомата показан на рис. 1.8, на котором вместо многих «параллельных» дуг с разными пометками нарисована одна дуга со всеми пометками.

Находясь в состоянии g₀¹, автомат передвигает первую головку к началу второго слова и, обнаружив его, переходит в состояние q₁¹. Если конец ленты # встречается раньше символа *, автомат переходит в незаключительное состояние q₆². Если же автомат приходит к состоянию q₁¹, он считывает поочередно символы второго слова первой головкой (состояние q₁¹), а символы первого слова — второй головкой (состояния q₃² и q₅²), сравнивая эти символы. Автомат возвращается каждый раз в состояние q₁¹, если символы одинаковы. Если же обнаружится несовпадение символов или первая головка встречает конец слова раньше символа *, автомат уходит в состояние q₆². Попав в это состояние, автомат не может выйти из него; перемещая вторую головку к концу слова на ленте, он достигает #, находясь в незаключительном состоянии, так что слово на ленте отвергается. Если первая головка достигнет конца второго слова, а вторая головка обнаружит, что первое слово тоже просмотрено до конца, то автомат перейдет в заключительное состояние q₇¹. В противном случае автомат перейдет в состояние q₆², отвергая слово.

Этот пример легко обобщить на случай произвольного алфавита V, увеличивая количество состояний множества Q.