Одноленточные автоматы

Конечный одноленточный (детерминированный, односторонний) автомат обнаруживают ряд полезных качеств, используемых в теории схем программ для установления разрешимости свойств ССП.

Одноленточный конечный автомат (ОКА) над алфавитом V задается набором: A = {V, Q, R, q₀, #, I} и правилом функционирования, общим для всех таких автоматов. В наборе А:

V - алфавит;

Q - конечное непустое множество состояний (Q V=Æ);

R - множество выделенных заключительных состояний (R Q);

q₀ - выделенное начальное состояние;

I - программа автомата;

# - «пустой» символ.

Программа автомата I представляет собой множество команд вида qа q', в которой q,q' Q, a V и для любой пары (q, a) существует единственная команда, начинающаяся этими символами.

Неформально ОКА можно представить как абстрактную машину, похожую на машину Тьюринга, но имеющую следующие особенности:

1) выделены заключительные состояния;

2) машина считывает символы с ленты, ничего не записывая на нее;

3) на каждом шаге головка автомата, считав символ с ленты и перейдя согласно программе в новое состояние, обязательно передвигается вправо на одну клетку;

4) автомат останавливается в том и только в том случае, когда головка достигнет конца слова, т.е. символа #.

Говорят, что автомат допускает слово a в алфавите V, если, начав работать с лентой, содержащей это слово, он останавливается в заключительном состоянии. Автомат A задает характеристическую функцию множества M_A допускаемых им слов в алфавите V, т. е. он распознает, принадлежит ли заданное слово множеству M_A если связать с остановкой в заключительном состоянии символ 1, а с остановкой в незаключительном состоянии – 0.

Наглядным способом задания ОКА служат графы автоматов. Автомат А представляется графом, множество вершин которого – множество состояний Q, и из вершины q в вершину q’ ведет дуга, помеченная символом а, тогда и только тогда, когда программа автомата содержит командуqа q'. Работе автомата над заданным словом соответствует путь из начальной вершины q. Последовательность проходимых вершин этого пути – это последовательность принимаемых автоматом состояний, образ пути по дугам – читаемое слово. Любой путь в графе автомата, начинающийся в вершине q₀ и заканчивающийся в вершине q R, порождает слово, допустимое автоматом.

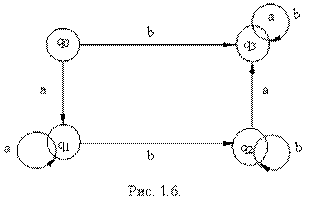
Пример 1.2. ОКА A = ({a, b}, {q₀, q₁, q₂, q₃}, {q₂}, q₀, #, I), допускающего слова {aⁿ b^m | n = 1,2, ...; m = 1,2, ...}, задается графом (рисунок 1.6.). Программа I содержит команды:

q₀a q₁; q₀b q₃; q₁a q₁; q₁b q₂; q₂a q₃; q₂b q₂; q₃a q₃; q₃b q₃.

Автомат называется пустым, если М_А = Æ, Автоматы А1 и А2 эквивалентны, если М_А1 = М_А2. Для машины Тьюринга проблемы пустоты и эквивалентности неразрешимы, более того, они не являются частично разрешимыми. Ситуация меняется для конечных автоматов.

Для ОКА доказано:

1) Проблема пустоты ОКА разрешима.

Доказательство основано на проверке допустимости конечного множества всех слов, длина которых не превышает числа состояний ОКА - n. Если ни одно слово из этого множества не допускается, то ОКА «пуст».

2) Предположение о том, что минимальная длина допускаемого слова больше n отвергается на том основании, что оно может быть сведено к слову меньшей длины, путем выбрасывания участков между двумя повторяющимися в пути узлами.

3) Проблема эквивалентности ОКА разрешима.

Доказательство основано на использовании отношения эквивалентности двух состояний q и q': если состояния q и q' эквивалентны, то для всех a A состояния d(q, a) и d'(q', a) также эквивалентны. Формируемые пары не должны входить одновременно заключительное и незаключительное состояния.