Двоичный двухголовочный автомат

Cтандартные схемы могут моделировать (в уточненном ниже смысле) двухголовочные автоматы, что позволяет свести проблему пустоты этих автоматов к проблеме пустоты схем. Такое моделирование можно осуществить более простым способом, если использовать специальный класс двухголовочных автоматов, а именно класс двоичных автоматов, работающих со словами над алфавитом {0, 1}. Следующая лемма устанавливает связь между классом всех двухголовочных автоматов и специальным подклассом двоичных автоматов.

Лемма. Существует алгоритм преобразования двухголовочных автоматов в двоичные двухголовочные автоматы (ДДКА), сохраняющий пустоту автоматов(построенный двоичный автомат А_b пуст тогда и только тогда, когда пуст исходный автомат А).

Доказательство. Пусть ДКА А над алфавитом V = {a₁, a₂, ...a_n} имеет множество состоянийQ_А = {q₁^k, q₂^k, …, q_k^k}, где верхний индекс (k = 1, 2) определяет номер активной головки. Преобразование этого автомата в двоичный начнем с кодировки символов и слов из V* словами в алфавите {0, 1} по следующему правилу:

код (#) = 0;

код (a_i) = 11....10 (i = 1, …, n);

код (aa_i) = код (a) код (a_i).

Так как символ # кодируется нулем, то любому непустому слову на ленте автомата А соответствует двоичное слово на ленте автомата А_b, оканчивающееся двумя нулями. Автомат останавливается, прочитав два нуля подряд (или 0, означающий пустое слово).

Автомат A преобразуется в двоичный автомат A_b так, как показано на графах рисунка 1.9. Каждый фрагмент графа А (рисунок 1.9, а) заменяется фрагментом (рисунок 1.9, б) для А_b.

После замены добавляются фрагменты (рисунок 1.9 в, г).

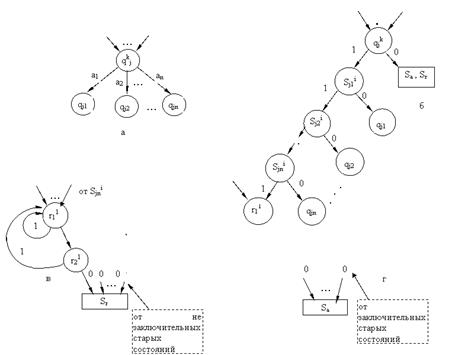
Множество состояний автомата А_b включает:

а) все старые состояния из Q_А;

б) для каждого старого состояния q_j^kn новых состояний, n - число символов алфавита V;

в) два новых состояния r₁¹ и r₂¹.

Заключительными состояниями автомата А являются заключительные состояния автомата А_b.

Вершины S_a (останов допускающий) и S_r (останов отвергающий) носят на графе вспомогательный характер в графе А_b.Они отмечают тот факт, что автомат прочитал два нуля подряд и остановился в заключительном состоянии (случай S_a) или в незаключительном состоянии (случай S_r).

Легко убедиться, что автомат А_ь допускает двоичное слово р тогда и только тогда, когда оно является двоичным кодом слова из V*, допускаемого автоматом А. Таким образом, из пустоты автомата А следует пустота автомата А_ь, и наоборот.

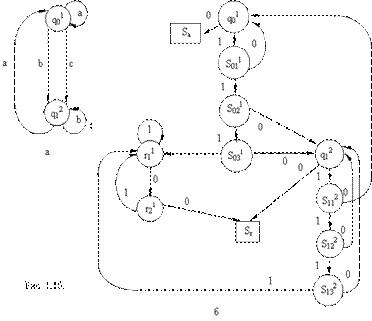
На рисунке 1.10, а приведен граф ДКА A допускающий только те слова в алфавите V = {a, b, c}, в которых символ a встречается не меньшее число раз, чем символы b и c, вместе взятые. Заключительное состояние R={q₀¹}. На рисунке 1.10, б приведен граф ДДКА, построенный по автомату А (10 – код символа a, 110 – код b, 1110 – код c).

По заданному ДДКА возможно построить ССП и наоборот, что позволяет решить задачу разрешимости (не разрешимости) свойств ССП, так как эта задача для ДДКА решена.