Эквивалентность, тотальность, пустота, свобода

ССП S в базисе В тотальна (пуста), если для любой интерпретации I базиса В программа (S, I) останавливается (зацикливается).

Стандартные схемы S₁, S₂ в базисе В функционально эквивалентны (S₁ ~ S₂), если либо обе зацикливаются, либо обе останавливаются с одинаковым результатом, т. е. val(S₁, I) » val(S₂, I).

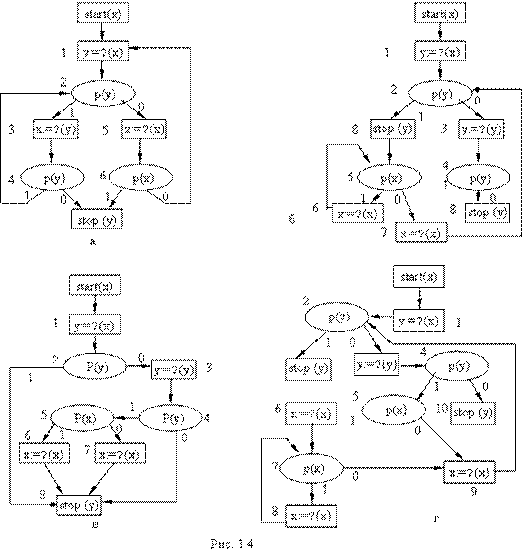
Примеры тотальных, пустых и эквивалентных схем S₂, S₃, S₄, S₅ приведены на рисунке 1.4.

Цепочкой стандартной схемы(ЦСС) называют:

1. конечный путь по вершинам схемы, ведущий от начальной вершины к заключительной;

2. бесконечный путь по вершинам, начинающийся начальной вершиной схемы.

В случае, когда вершина-распознаватель (v), то дополнительно указывается верхний индекс (1 или 0), определяющий 1-дугу или 0-дугу, исходящую из вершины.

Примеры цепочек схемы S₁ (рисунок 1.3,а): (0, 1, 2¹, 5); (0, 1, 2⁰, 3, 4, 2⁰ 3, 4, 2¹, 5) и т. д.

Цепочкой операторов(ЦО) называется последовательность операторов, метящих вершины некоторой цепочки схемы.

Например для S₁: (start(х), у:=a, р¹(x), stop(у)) или (start(х), у:=a, р⁰(x), y:=g(x, y), x:=h(x), р⁰(x), y:=g(x, y), x:=h(x), р⁰(x), y:=g(x, y), x:=h(x), …)) и т. д.

Предикатные символы ЦО обозначаются так же, как вершины распознавателей в ЦСС.

Пусть S - ССП в базисе В, I - некоторая его интерпретация, (0, 1, …, l₂, l₃,…) - последовательность меток инструкций S, выписанных в том порядке, в котором эти метки входят в конфигурации протокола выполнения программы (S, I). Ясно, что эта последовательность – цепочка схемы S. Считают, что интерпретация I подтверждает (порождает) эту цепочку.

ЦСС в базисе В называют допустимой, если она подтверждается хотя бы одной интерпретацией этого базиса.

Не всякая ЦСС является допустимой. В схеме S₂ (рисунок 1.4,а) цепочки(0, 1, 2⁰, 5, 6¹, 7), (0, 1, 2¹, 3, 4⁰, 7) и все другие конечные цепочки не подтверждаются ни одной интерпретацией.

Свойство допустимости цепочек играет чрезвычайно важную роль в анализе ССП. В частности оно определяет те случаи, когда стандартная схема свободна.

ССП свободна, если все ее цепочки допустимы.

Допустимая цепочка операторов - это цепочка операторов, соответствующая допустимой цепочке схемы. В тотальной схеме все допустимые цепочки (и допустимые цепочки операторов) конечны. В пустой схеме - бесконечны.

Рассмотренные свойства распространяются на все другие классы стандартных схем и образуют опорные пункты схематологии программирования.