Интерпретация стандартных схем программ
ССП не является записью алгоритма, поэтому позволяет исследовать только структурные свойства программ, но не семантику вычислений. При построении «семантической» теории схем программ вводится понятие интерпретация ССП. Определим это понятие.
Пусть в некотором базисе В определен класс ССП. Интерпретацией базиса В в области интерпретации D называется функция I, которая сопоставляет:
1.каждой переменной х из базиса В - некоторый элемент d = I(x) из области интерпретации D;
2.каждой константе а из базиса В - некоторый элемент d = I(а) из области интерпретации D;
3.каждому функциональному символу f (n) - всюду определенную функцию F(n) = I(f (n));
4.каждой логической константе р(0) - один символ множества {0,1};
5.каждому предикатному символу р(n) - всюду определенный предикатP (n)= I(p(n)).
Пара (S,I) называется интерпретированной стандартной схемой (ИСС), или стандартной программой (СП).
Определим понятие выполнения программы.
Состоянием памяти программы (S,I) называют функцию W: XS  D, которая каждой переменной x из памяти схемы S сопоставляет элемент W(x) из области интерпретации D.
D, которая каждой переменной x из памяти схемы S сопоставляет элемент W(x) из области интерпретации D.
Значение терма τ при интерпретации I и состоянии памяти W (обозначим τI(W)) определяется следующим образом:
1) если τ = х, x – переменная, то τI(W) = W(x);
2) если τ = a, a – константа, то τI(W) = I(a);
3) если τ = f(n)(τ1, τ2..., τn), то τI(W) = I(f (n))(τ1I(W), τ2I(W),..., τnI(W)).
Аналогично определяется значение теста p при интерпретации I и состоянии памяти W или pI(W):
если p = р(n)(τ1, τ2,..., τn), то pI(W) = I(p(n))(τ1I(W), τ2I(W),... τnI(W)), n ≥ 0.
Конфигурацией программы называют пару U = (L,W), где L - метка вершины схемы S, а W - состояние ее памяти. Выполнение программы описывается конечной или бесконечной последовательностей конфигураций, которую называют протоколом выполнения программы (ПВП).
Протокол (U0, U1,..., Ui, Ui+1,...) выполнения программы (S,I) определяем следующим образом (ниже kiозначает метку вершины, а Wi - состояние памяти в i-й конфигурации протокола, Ui = (ki,Wi)): U0 = (0, W0), W0 – начальное состояние памяти схемы S при интерпретации I.
Пусть Ui = (ki, Wi) - i-я конфигурация ПВП, а О - оператор схемы S в вершине с меткой ki. Если О - заключительный оператор stop(τ1, τ2... τn), то Ui - последняя конфигурация, так что протокол конечен. В этом случае считают, что, программа (S,I) останавливается, а последовательность значений τ1I(W), τ2I(W),..., τnI(W) объявляют результатом val(S,I) выполнения программы (S,I). В противном случае, т. е. когда О - не заключительный оператор, в протоколе имеется следующая, (i+1)-я конфигурация Ui+1 = (ki+1, Wi+1), причем
а) если О - начальный оператор, а выходящая из него дуга ведет к вершине с меткой L, то ki+1 = L и Wi+1 = Wi;
б) если О - оператор присваивания х:= τ, а выходящая из него дуга ведет к вершине с меткой L, то ki+1 = L, Wi+1 = Wi, Wi+1(х) = τ1(Wi);
в) если О - условный оператор p и pI(Wi) = Δ, где Δ  {0,1}, а выходящая из него дуга ведет к вершине с меткой L, то ki+1 = L и Wi+1 = Wi;
{0,1}, а выходящая из него дуга ведет к вершине с меткой L, то ki+1 = L и Wi+1 = Wi;
г) если О - оператор петли, то ki+1 = L и Wi+1 = Wi, так что протокол бесконечен.
Таким образом, программа останавливается тогда и только тогда, когда протокол ее выполнения конечен. В противном случае программа зацикливается и результат ее выполнения не определен.
Рассмотрим две интерпретации СПП S1 (рисунок 1.2, а). Интерпретация(S1, I1) задана так:
1.область интерпретации D1 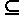 Nat - подмножество множества Nat целых неотрицательных чисел;
Nat - подмножество множества Nat целых неотрицательных чисел;
2.I1(x)=4; I1(y)=0; I1(a)=1;
3.I1(g)=G, где G - функция умножения чисел, т. е. G(d1,d2)= d1*d2;
4.I1(h)=H, где H - функция вычитания единицы, т. е. H(d)= d - 1;
5.I1(p)=P1, где P1 - предикат «равно 0», т.е. P1(d)=1, если d=0.
Программа (S1, I1) вычисляет 4! (рисунок 1.3, б).
Интерпретация (S1, I2) задана следующим образом:
1.область интерпретации D2=V*, где V = {a, b, c}, V* - множество всех возможных слов в алфавите V.
2.I2(x)=abc;
3.I2(y)=e, где e - пустое слово;
4.I2(a)= e;
5.I2(g)=CONSTAR;
6.I2(h)=CDR;
7.I2(p)=P2, где P2 - предикат «равное e», т.е. P2(a)=1, если a=e.
Программа (S1, I2) преобразует слово abc в слово cba (рисунок 1.3, в).
ПВП (S1, I1) и (S1, I2) конечен, результат - 24 и - cba (таблица 1.1 и 1.2).
Табл. 1.1.
| Конфигурация | U0 | U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | U10 | U11 | U12 | U13 | |
| Метка | |||||||||||||||
| Значения | х | ||||||||||||||
| у |
Табл. 1.2.
| Конфигурация | U0 | U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | U10 | U11 | U12 | |||||||
| Метка | ||||||||||||||||||||
| Значения | x | abc | abc | abc | abc | bc | bc | bc | c | c | c | e | e | e | ||||||
| у | e | e | e | a | a | a | ba | ba | ba | cba | cba | cba | cba | |||||||
Дата добавления: 2015-07-18; просмотров: 1422;
