Метод расчета сравнительной эффективности инвестиций.

Используется в следующей ситуации: И₁ > И₂; 3₁ < 3₂ (C_c1< C_c2).

Сущность метода:определение эффективности дополнительных
инвестиций по одному из вариантов. При этом можно использовать
два показателя.

1. Срок окупаемости дополнительных инвестиций. Срок окупа-
емости дополнительных инвестиций определяет период времени, за
который дополнительные инвестиции по одному из проектов окупят-
ся снижением себестоимости продукции по этому проекту:

2. Коэффициент сравнительной эффективности инвестиций:

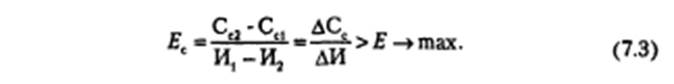
По экономическому содержанию ∆С_c — дополнительная прибыль
по одному из вариантов, возникающая вследствие более низкой себе-
стоимости. Коэффициент сравнительной эффективности инвестиций

определяет доходи ость дополнительных инвестиций за счет снижения
себестоимости.

Общая оценка метода дана в табл. 73.

Методы, основанные на дисконтированных оценках с теоре-
тической точки зрения, являются более обоснованными, поскольку
учитывают фактор времени. Вместе с тем они относительно более тру-
доемки в вычислительном плане. Из всех рассмотренных критериев
наиболее приемлемыми для принятия решений инвестиционного
характера являются методы расчета NPV. ИД и ВНД. Вариант,
у которого эти показатели максимальны, будет лучшим.

Однако несмотря на отмеченную взаимосвязь между этими пока-
зателями. при оценке альтернативных инвестиций проблема выбора
критерия остается, так как чаще всего результаты расчетов про-
тиворечат друг другу. Рассмотрим это на примере.

Пример 7.2. Выберем лучший вариант инвестиционного проекта из трех
альтернативных инвестиций при норме дисконта Е= 10% (рис. 7.2).

Выводы по расчетам.

1. Максимальный NPV - 105 д.е. имеет проект 2, т.е. реализа-
ция этого проекта дает наибольший прирост капитала фирмы.

2. Максимальный индекс доходности ИД» 1,455 д.е./д.е у про-
екта 1. т.е. текущая стоимость денежного потока на 45,5% превыша-
ет величину стартового капитала.

3. Максимальную внутреннюю норму доходности ВНД=35,4%
имеет проект 3.

Следовательно, каждый проект имеет максимальное значение
одного из критериев.

Таким образом, при анализе альтернативных проектов критерии
NPV, ИД и ВНД могут противоречить друг другу и сложно опреде-
лить лучший проект. Причины возникновения противоречия между
критериями:

масштаб проекта, т.е значительное отличие элементов денеж-
ных потоков одного проекта от элементов другого проекта;

интенсивность потока денежных средств, т.е. временное рас-
пределение максимальных денежных потоков на первые или преиму-
щественно на последние годы жизни проекта.

В случае противоречивости показателей за основу следует брать
NPV, так как он характеризует возможный прирост «цены фирмы»,
обладает свойством аддитивности, что позволяет складывать NPV по
различным проектам. Однако у показателя NPV есть существенный
недостаток: его зависимость от нормы дисконта Е, т.е. при разных
значениях нормы дисконта можно получить совершенно противопо-
ложные результаты.

Для более достоверного анализа инвестиционных проектов реко-
мендуется использовать график зависимости NPV от нормы дисконта
NPV =f(Е), который:

- представляет нелинейную зависимость;

- пересекает ось Y в точке NPV = f(Е =0), т.е. NPV₀ = SД - SИ
(недисконтированные);

- пересекает ось X в точке, соответствующей ВНД проекта.

Пример 7.3. Продолжим решение примера 7.2. Из дальнейшего
рассмотрения исключим проект 1, поскольку его NPV и ВНД самые
низкие, а ИД чуть выше, чем у проектов 2 и 3.

Показатели проектов 2 и 3 противоречивы, поэтому проведем
анализ с помощью графиков NPV = f(Е). Для их построения прове-
дем дополнительные расчеты:

Из рисунка 7.3 видно, что выбор проекта для реализации зави-
сит от принятой ставки Е. При Е = 10% лучшим является проект 2,
однако если бы норма дисконта Е была равна 20%. то лучшим стал
бы проект 3.

Кривые на рис. 7.3 имеют точку- пересечения, которая называется
пересечением (или точкой) Фишера (по имени известного экономи-
ста Ирвинга Фишера, проанализировавшего этот аспект инвестици-
онных расчетов). Характеристики точки Фишера:

1) показывает значение нормы дисконта Е, при которой альтерна-
тивные проекты имеют одинаковое значение NPV;

2) пограничная точка, разделяющая ситуации, «улавливаемые»
критерием NPV и «не улавливаемые» критерием ВНД:

— если Е > точки Фишера, то NPV и ВНД не противоречат друг
другу и оба показывают лучший проект;

— если Е< точки Фишера, то NPV и ВНД противоречат друг дру-
гу и лучший проект определяется по максимальному значению NPV.

Причем критерий NPV позволяет выявить лучший вариант в лю-
бой ситуации.

Значение нормы дисконта Е в точке Фишера численно равно ВНД
приростного потока, т.е. потока, составленного из разностей соответ-
ствующих элементов исходных потоков. Для нахождения точки
Фишера необходимо:

— составить гипотетический проект (приростный поток);

— найти ВНД этого потока.

Пример 7.4. Вернемся к примерам 7.2 и 7.3 и определим точку

Фишера для проектов 2 и 3.

Составим гипотетический (приростный) поток (рис. 7.4).