Основные характеристики цикла и предел усталости

Рассмотрим вначале случай одноосного напряженного состояния.

Закон изменения главного напряжения о во времени представлен кривой, показанной на рис. 6.

Наибольшее и наименьшее напряжения цикла обозначим через 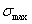и . И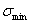х отношение называется коэффициентом цикла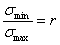

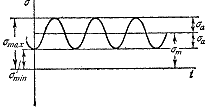
Рис.6. Закон изменения главного напряжения во времени.

В случае, когда 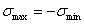, и цикл называется симметричным. Такой цикл, в частности, имеет место в рассмотренном выше примере вращающейся оси вагона.) Если 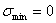или же 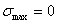, цикл называется пульсационным (рис. 7). Для пульсационного цикла r = 0 или 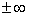. Циклы, имеющие одинаковые показатели r, называются подобными.

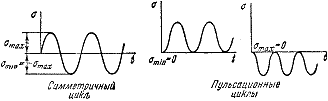
Рис.7. Симметричный а) и пульсационные б) циклы

Любой цикл может быть представлен как результат наложения постоянного напряжения 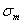на напряжение, меняющееся по симметричному циклу с амплитудой 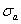(рис. 6). Очевидно, при этом:

,

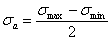
(1)

Считается общепризнанным, что усталостная прочность детали не зависит от закона изменения напряжений внутри интервала 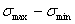. Поэтому между циклами, показанными, например, на рис. 8, различия не делается. Точно та к же считается несущественным и влияние частоты изменения цикла. В итоге цикл определяется только величинам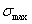и и 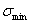или же 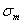и .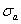

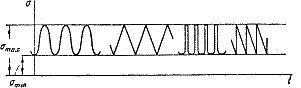
Рис.8. Виды пульсаций в циклах.

Теперь перейдем к механическим характеристикам материала. И условиях циклических напряжений они определяются путем специальных испытаний.

Наиболее распространенными являются испытания в условиях симметричного цикла. При этом обычно используется принцип чистого изгиба вращающегося образца (рис. 9).

Рис.9. Модель усталостного испытания.

Для испытаний в условиях несимметричных циклов используются либо специальные машины, либо же вводятся дополнительные приспособления. Так, например, можно на испытуемом образце установить пружину, создающую постоянное растяжение образца с напряжением 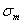. Во время испытания на это напряжение накладывается напряжение от изгиба, меняющееся по симметричному циклу.

Путем многократных испытаний (если имеется достаточное количество образцов) можно определить число циклов, которое выдерживает образец до разрушения, в зависимости от величины 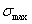цикла. Эта зависимость имеет вид кривой, показанной на рис.10

В связи с тем, что число циклов с уменьшением 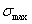возрастает в высокой степени, предпочитают в ряде случаев по оси абсцисс откладывать не число N а его логарифм.

Опыт показывает, что для большинства черных металлов можно указать такое наибольшее максимальное напряжение, при котором материал не разрушается при любом числе циклов. Такое напряжение называется пределом усталости, или пределом выносливости.

Предел выносливости обозначается через , где индекс r соответствует коэффициенту цикла. Так, для симметричного цикла обозначение предела выносливости принимает вид 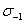, для пульсирующего или 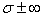. и т. д.

Рис.10. Зависимость числа циклов разрушения от максимального напряжения.

Для цветных металлов и для закаленных до высокой твердости сталей не удается установить такое число циклов, выдержав которое, образец не разрушился бы в дальнейшем. Поэтому в подобных случаях вводится понятие условного предела выносливости. За условный предел выносливости принимается напряжение, при котором образец способен выдержать 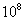циклов.

Определение предела выносливости является трудоемкой операцией, поэтому был сделан ряд попыток связать эмпирическими формулами предел выносливости с известными механическими характеристиками материала.

Обычно считается, что для сталей предел выносливости при изгибе составляет половину от предела прочности:

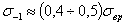
Для высокопрочных сталей можно принять:

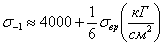
Для цветных металлов предел выносливости изменяется в более широких пределах:

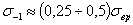
Аналогично испытанию на чистый изгиб можно вести испытание «а кручение в условиях циклически изменяющихся напряжений. В этом случае:

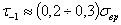
Указанные соотношения и все им подобные следует, однако, применять с большой осторожностью, поскольку они получены только для определенных материалов и в определенных условиях испытаний (при изгибе, при кручении).

В связи с этим следует указать, что предел усталости не является характеристикой только свойств материала, как, например, модуль упругости или коэффициент Пуассона. Он зависит также от метода ведения испытаний. Расчетное напряжение для образца не определяет полностью процесс усталостного разрушения. В результате образования трещины величина напряжений и законы их распределения в образце непрерывно меняются в зависимости от условий дальнейшего развития трещины. Последние же в свою очередь зависят от абсолютных размеров образца и характера приложения внешних сил. Все это неминуемо сказывается на предельном числе циклов и на величине предела усталости.

В результате указанных обстоятельств, например, предел усталости, полученный в условиях циклического растяжения и сжатия, оказывается на 10—20% ниже, чем предел усталости, полученный при изгибе. Предел усталости при кручении сплошных образцов отличается от предела усталости, полученного для полых образцов, и т. п.

Лекция № 46. Диаграмма усталостной прочности.

Положим, имеется машина, на которой можно производить усталостные испытания в условиях любого несимметричного цикла. Задавая постоянное значение 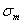, находим путем последовательных испытаний образцов такое наибольшее значение амплитуды 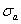, при котором материал способен еще выдержать неограниченное число циклов. Если для взятого материала такого предельного напряжения не существует, величина 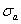определяется по условному базовому числу N.

В результате проведенной серии испытаний устанавливается предельное значение 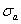, соответствующее некоторому напряжению 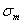. Полученный результат может быть графически изображен точкой в системе координат 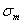, 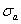( рис. 438). Сумма координат этой точки дает предельное максимальное напряжение цикла, т. е. предел усталости , где:

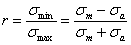
Продолжая такие испытания и дальше, получаем множество точек, через которые проводится предельная кривая, характеризующая прочностные свойства материала в условиях несимметричных циклов. Эта кривая носит название диаграммы усталостной прочности (рис. 1).

Точки А к С диаграммы соответствуют пределам прочности.при простом растяжении и сжатии. Точка В отражает результаты испытания в условиях симметричного цикла.

Полученная диаграмма дает возможность судить о прочности конструкции, работающей при циклически изменяющихся напряжениях.

Положим, для некоторой детали цикл характеризуется значениями напряжени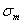й и 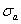. Эти величины могут рассматриваться как координаты рабочей точки в плоскости 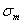, 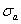. Если рабочая точка располагается ниже предельной кривой, рассматриваемая деталь может в условиях циклически изменяющихся напряжений работать неограниченно долго. Если рабочая точка оказывается выше предельной кривой, деталь разрушится после некоторого числа циклов.

Так как построение диаграммы усталостной прочности связано с весьма трудоемкими испытаниями, предпочитают обычно полученную кривую АВС заменять двумя прямыми АВ и ВС, как это отмечено пунктиром на рис. 2. Рабочая область при этом несколько сокращается, что дает погрешность в запас прочности.

Рис.1. Реализация предельного напряжения.

Рис.2. Диаграмма усталостной прочности.

Одновременно отсекается сомнительная зона разброса экспериментальных точек.

Для построения упрощенной диаграммы достаточно располагать пределом усталости при симметричном цикле 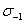, и иметь значения пределов прочност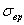и и .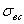

Рабочая точка в плоскости 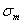, 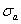не может занимать произвольное положение. Она должна находиться в области осуществимых циклов, которая определяется следующими очевидными условиями:

и

Так как:

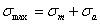, а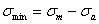

то область осуществимых циклов имеет верхнюю границу в виде двух прямых:

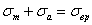и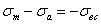

Эти прямые вместе образуют треугольник АСD (рис.3), который и представляет собой область осуществимых циклов.

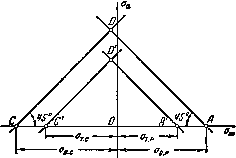
Рис.3. Область осуществимых циклов

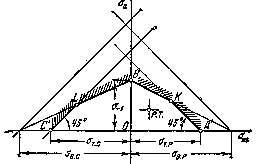
Рис.4. Область допустимых циклов с ограничениями на пластические деформации.

Для пластичных материалов таким же способом может быть отмечена область упругих деформаций. Граница этой области очерчивается сверху прямым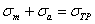и:

и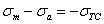

В результате получаем треугольник 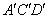(рис. 3).

Если рабочая точка оказывается в пределах этого треугольника» пластические деформации в детали не возникают. Рабочая точка, находящаяся за пределами треугольника А'С'D', но остающаяся внутри треугольника АСD, свидетельствует о том, что в детали возникают пластические деформации. Если, наконец, рабочая точка оказывается за пределами треугольника АСD, при первом же цикле происходит разрушение детали.

При расчетах конструкций, предназначенных на длительные сроки службы, напряжения цикла ограничиваются как по условиям усталостной прочности, так и по условиям недопущения пластических деформаций. Поэтому, объединяя диаграммы, показанные на рис. 2 и 3, получаем рабочую область в виде многоугольника А'КВLС' (рис.4). Рабочая точка (р. т.) исследуемого цикла для рассчитываемой детали должна находиться в пределах указанного многоугольника.

Теперь возникает вопрос, как определить координаты рабочей точки и как определить коэффициент запаса детали в условиях циклического нагружения. Оба эти вопроса содержат в своем решении ряд специфических особенностей, к рассмотрению которых сейчас и перейдем.

Лекция № 47. Расчет коэффициентов запаса усталостной прочности.

Одним из основных факторов, которые необходимо учитывать при практических расчетах на усталостную прочность, является фактор местных напряжений.

а) растяжение, б) изгиб, в) контактные напряжения

Рис.1. Очаги концентрации местных напряжений:

Многочисленные теоретические и экспериментальные исследования показывают, что в области резких изменений в форме упругого тела (входящие углы, отверстия, выточки), а также в зоне контакта деталей возникают повышенные напряжения с ограниченной зоной распространения, так называемые местные напряжения.

Например, при растяжении полосы с небольшим отверстием рис. 1, а) закон равномерного распределения напряжений вблизи отверстия нарушается. Напряженное состояние становится двухосным, а у края отверстия появляется пик напряжения. Аналогично при изгибе ступенчатого стержня (рис. 1, б) в зоне входящего угла возникает повышенное напряжение, величина которого зависит в первую очередь от радиуса закругления r. При прессовой посадке втулки на вал (рис. 1, в) у концов втулки и вала также возникают местные напряжения. Подобных примеров можно привести очень много.

Величина местных напряжений в зависимости от геометрической формы детали определяется обычно теоретически при помощи методов математической теории упругости.

Основным показателем местных напряжений является теоретический коэффициент концентрации напряжений:

Рис.2. Зона расчета номинального напряжения

где 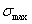— наибольшее местное напряжение, а 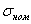—так называемое номинальное напряжение. Это — то напряжение, которое определяется по формулам сопротивления материалов без учета эффекта концентрации. Обычно подсчет 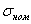ведется по наиболее ослабленному сечению детали, как, например, по сечению АА (рис. 2).

Например, для полосы с отверстием (рис. 1, а)

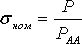
для случая изгиба ступенчатого стержня (рис. 1, б)

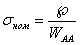
Однако, если при подобных подсчетах возникают трудности, за номинальное принимается напряжение в неослабленном сечении. Например, при кручении вала, имеющего поперечное отверстие (рис. 2), имеем:

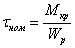
где 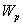— полярный момент сопротивления неослабленного сечения.

Так или иначе, номинальное напряжение выбирается в первую очередь из соображений, связанных с простотой расчета.

Величина теоретического коэффициента концентрации определена для большинства встречающихся на практике типовых конструктивных элементов.

Рис.3. Определение коэффициента концентрации для полосы с отверстием — а), с использованием графика — б)

Данные по величине приводятся в виде таблиц; в справочной литературе по машиностроению. Так, например, на рис. 3 показана зависимость теоретического коэффициента концентрации от соотношения геометрических размеров полосы с отверстием.

Наличие местных напряжений оказывает на прочность детали различное влияние в зависимости от свойств материала и от характера нагружения. В связи с этим в отличие от теоретического вводится понятие эффективного коэффициента концентрации , причем делается различие между постоянными и циклически изменяющимися напряжениями.

При постоянных напряжениях (при r=1) под эффективным коэффициентом концентрации понимается отношение

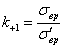
где 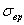—предел прочности для образца, не имеющего очагов концентрации, а 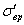—условный предел прочности для образца, обладающего очагами концентрации напряжений.

При испытании, например, призматического стержня с отверстием (рис. 4, а) эффективный коэффициент концентрации напряжений вблизи отверстия определяется отношением разрушающей нагрузки Р к разрушающей нагрузке Р'. То же самое имеет место и для образца с выточкой (рис. 4, б).

Для пластичных материалов местные напряжения в условиях постоянной нагрузки не оказывают на прочность детали существенного влияния. Обычно в зоне повышенных напряжений образуются местные пластические деформации без образования трещины, Весь остальной объем тела за пределами этой зоны работает упруго, и несущая способность сохраняется практически до тех же значений сил, что и при отсутствии очагов концентрации. Это дает право при статическом нагружении не учитывать местных напряжений.

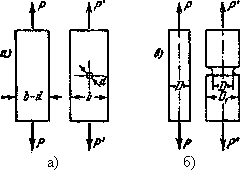
Рис.4. эффект концентрации местных напряжений для детали с отверстием — а) и с выточкой — б)

Таким образом, можно считать, что для пластичных материалов: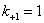

Для хрупких материалов значение 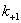приближается к значению теоретического коэффициента концентрации 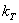. Здесь, правда, возможны исключения. Для чугуна, например, независимо от формы детали, 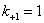. Объясняется это структурными особенностями чугуна, имеющего в своей массе включения графита. Каждое включение является очагом концентрации, приводящим к существенно большим местным напряжениям, чем те, которые обусловливаются конструктивными факторами (выточками, отверстиями и пр.).

В условиях циклически изменяющихся напряжений (при ) эффективный коэффициент концентрации определяется отношением:

где 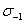— предел усталости гладкого образца, а 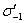—предел усталости образца, имеющего очаги концентрации напряжений.

Величина 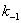, также как и 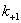зависит не только от геометрической формы детали, но и от механических свойств материала. Концентрация напряжений существенно сказывается на усталостной прочности и хрупких и пластичных материалов, поскольку и в том и в другом случае при многократном изменении напряжений разрушение начинается с образования местной трещины.

Числовое значение эффективного коэффициента концентрации может быть определено только на основе усталостного испытания большого числа образцов из различных материалов. В настоящее время в этом направлении накоплен достаточно большой экспериментальный материал. Сопоставление полученных результатов позволяет в некоторой ограниченной мере установить соотношение между эффективным и теоретическим коэффициентами концентрации в виде

(13.6)

где q — так называемый коэффициент чувствительности материала к местным напряжениям.

Величина q зависит в основном от свойств материала. Так, например, можно считать, что для высокопрочных легированных сталей величина q близка к единице. Для конструкционных сталей в среднем 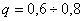, причем более прочным стал ям соответствуют большие значения q. Для чугуна q = 0 и .

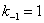Коэффициент чувствительности зависит также в некоторой степени и от геометрических особенностей очага концентрации. Наблюдается некоторое снижение q в случае больших коэффициентов .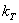

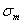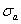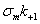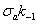При расчетах на усталостную прочность наличие местных напряжений учитывается путем введения поправок в числовые значения координат рабочей точки ( р. т.) на диаграмме усталостной прочности. Так, если расчет детали по номинальным напряжениям дает характеристики цикла и , то с учетом местных напряжений следует соответственно принять значения координат рабочей точки в виде и , где 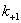принимается обычно равным единице.

Из всего изложенного следует, что наличие концентрации напряжений снижает усталостную прочность детали. Поэтому при проектировании машин следует стремиться к тому, чтобы влияние местных напряжений было сведено к минимуму. Достигается это, прежде всего, конструктивными мерами. Для ответственных деталей, работающих в условиях циклических напряжений, внешние обводы стремятся сделать возможно более плавными, радиусы закругления во внутренних углах увеличивают, необходимые отверстия располагают в зоне пониженных напряжений и т. д.

Рис.5. Конструкция галтели и проставочных колец

На рис. 5, а показана конструкция галтели с глубоким поднутрением, уменьшающим местные напряжения. Для увеличения радиуса галтели могут применяться также проставочные кольца, как это показано на рис. 5, б. Для снижения местных напряжений иногда практикуется введение разгрузочных канавок (рис. 6, а), наличие которых благотворно сказывается на усталостной прочности вала. Такого же рода разгрузочные канавки могут применяться и в местах посадки (рис. 6, б).

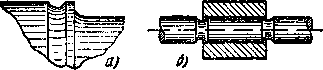
Рис.6. Конструкции разрушенных канавок — а), в том числе в местах посадок — б)