Уравнение Шредингера. Рассчитать волновые функции для конкретной задачи можно используя основное уравнение нерелятивистской квантовой механики сформулированное в 1926 г

Рассчитать волновые функции для конкретной задачи можно используя основное уравнение нерелятивистской квантовой механики сформулированное в 1926 г. Э. Шредингером.Решив его, мы находим набор энергетических уровней для заданной частицы, а также получаем информацию статистического характера о возможном положении частицы.

Уравнение Шредингера, как законы Ньютона и уравнения Максвелла, вывести нельзя. Оно основано на анализе экспериментальных данных и в масштабах атомов описывает волновые свойства частиц.

общее временное уравнение Шредингера для одномерного случая движения частицы с массой m, имеет вид:

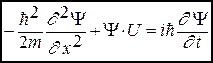, (229)

где 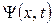– волновая функция. U(x,t) - силовая потенциальная функция, которая зависит от координаты и времени. Для трёхмерного случая уравнение (229) переходит в:

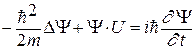(230)

Δ - оператор Лапласа:

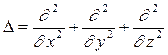
С помощью уравнений (229) и (230) можно описать вероятность перехода электрона на новые стационарные орбиты.

Знание Ψ-функции позволяет находить квадрат модуля Ψ функции - интенсивность волны де Бройля (плотность вероятности).

Условия решения уравнений (229) и (230):

1) Должна быть известна U(t)

2) Должна быть известна Ψ(x,0) или Ψ(x,y,z,0)

3) Граничные условия - знание поведения микрочастицы на границе: Ψ(0,t); Ψ(l,t)

4) Решением (229) и (230) является Ψ- функция, для которой справедливыстандартные условия, перечисленные выше.