Соотношение неопределенностей. В классической механике всякая частица движется по определенной тра­ектории, так что в любой момент времени точно фиксированы ее координата и импульс

В классической механике всякая частица движется по определенной тра­ектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микрочастицы из-за наличия у них волновых свойств существен­но отличаются от классических частиц. Одно из основных различий заключа­ется в том, что нельзя говорить о движении микрочастицы по определенной траттории и неправомерно говорить об одновременных точных значениях ее координаты и импульса. Это следует из корпускулярно-волнового дуализма. Так, понятие «длина волны в данной точке» лишено физического смысла, а поскольку импульс выражается через длину волны, то отсюда следует, что микрочастица с определенным импульсом имеет полностью неопределенную координату. И наоборот, если микрочастица находится в состоянии с точным значением координаты, то ее импульс является полностью неопределенным.

В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения вих поведении, пришел в 1927 г. к вы­воду, что объект микромира невозможно одновременно с любой наперед заданной точностью характеризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, р_у, p_z), причем неопределенности этих величин удовлетворяют условиям

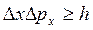
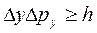(224)

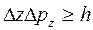
т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Следует отметить, что неравенство (224) не является точным. В литературе часто приводится формула 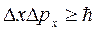. Она аналогична (224), но в её правой части стоит 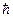— постоянная Планка «с чертой», называемая приведённой постоянной Планка. Между двумя этими формами записи нет противоречия: они обе справедливы только по порядку величины и обе годятся для качественных оценок. Более точное выражение имеет вид:

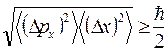
Здесь скобки 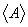обозначают дисперсию A.

В справочнике по физике это соотношение неопределенностей дается виде:

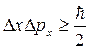(225)

Из соотношения неопределенностей (225) следует, что, например, если мик­рочастица находится в состоянии с точным значением координаты (Dх = 0), то в этом состоянии соответствующая проекция ее импульса оказывается со­вершенно неопределенной (Dр —>¥), и наоборот. Таким образом, для микро­частицы не существует состояний, в которых ее координаты и импульс име­ли бы одновременно точные значения. Отсюда вытекает и фактическая не­возможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта.

Принцип неопределённости не просто налагает ограничения на возможные результаты измерений. Он имеет более глубокий смысл и вскрывает новые для нас внутренние свойства самого объекта микромира: электрон не может одновременно иметь определённые значения проекций импульса и координаты на одно направление. Это заключение справедливо, конечно, не только для электрона, но и для любой частицы, локализованной в атомных масштабах (порядка ангстрема) и масса которой сравнима с массой атома.

В квантовой теории рассматривается также соотношение неопределенностей для энергии W и времени t. Неопределенности этих величин удовлетворяют условию:

(226)

где 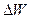- неопределенность энергии некоторого состояния системы, 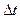-промежуток времени, в течение которого оно существует. Система. Имеющая среднее время жизни 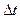, не может быть охарактеризована определенным значением энергии; разброс энергии 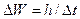возрастает с уменьшением среднего времени жизни. Из соотношения (226) также следует, что частота излучаемого фотона также должна иметь неопределенность 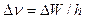, т.е. линии спектра должны характеризоваться частотой .

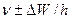Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.

Примечание

Дифракционные явления проявляются наиболее отчетливо, когда размеры препятствия, на котором происходит дифракция волн, соизмеримы с длиной волны. Это относится к волнам любой физической природы и, в частности, к электронным волнам. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.

Рассмотрим, например, дифракцию электронов на одиночной щели ширины D (рисунок 77). На графике справа приведено распределение электронов на фотопластинке. Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ₁ этого максимума находится из условия

D sin θ₁ = λ.

Это формула соответствует волновой теории.

С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение p_y поперечного импульса равно

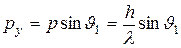
где p – модуль полного импульса электрона, равный, согласно де Бройлю, h / λ. Величина p при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ. Из этих соотношений следует

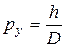
Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δy = D. Величину Δy называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна p_y или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δp_y. Таким образом, величины Δy и Δp_y связаны соотношением

Δy · Δp_y ≥ h,

которое называется соотношением неопределенностей Гейзенберга. Величины Δy и Δp_y нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой двигался какой-то конкретный электрон после прохождения щели и до фотопластинки в рассмотренном мысленном эксперименте.

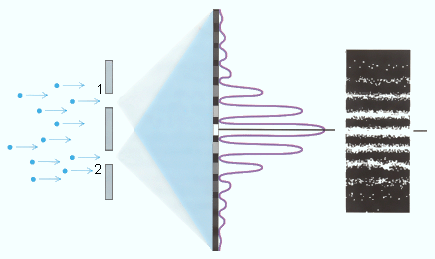
Рассмотрим еще один мысленный эксперимент – дифракцию электронного пучка на двух щелях (рис. 78). Схема этого эксперимента совпадает со схемой оптического интерференционного опыта Юнга.

Рисунок 78

Анализ этого эксперимента позволяет проиллюстрировать логические трудности, возникающие в квантовой теории. Те же проблемы возникают при объяснении оптического опыта Юнга, исходя из концепции фотонов.

Если в опыте по наблюдению дифракции электронов на двух щелях закрыть одну из щелей, то интерференционные полосы исчезнут, и фотопластинка зарегистрирует распределение электронов, продифрагировавших на одной щели (рисунок 77). В этом случае все электроны, долетающие до фотопластинки, проходят через единственную открытую щель. Если же открыты обе щели, то появляются интерференционные полосы, и тогда возникает вопрос, через какую из щелей пролетает тот или иной электрон?

Психологически очень трудно смириться с тем, что ответ на этот вопрос может быть только один: электрон пролетает через обе щели. Мы интуитивно представляем себе поток микрочастиц как направленное движение маленьких шариков и применяем для описания этого движения законы классической физики. Но электрон (и любая другая микрочастица) обладает не только корпускулярными, но и волновыми свойствами. Легко представить, как электромагнитная световая волна проходит через две щели в оптическом опыте Юнга, т. к. волна не локализована в пространстве. Но если принять концепцию фотонов, то мы должны признать, что каждый фотон тоже не локализован. Невозможно указать, через какую из щелей пролетел фотон, как невозможно проследить за траекторией движения фотона до фотопластинки и указать точку, в которую он попадет. Опыт показывает, что даже в том случае, когда фотоны пролетают через интерферометр поштучно, интерференционная картина после пролета многих независимых фотонов все равно возникает. Поэтому в квантовой физике делается вывод: фотон интерферирует сам с собой.

Все вышесказанное относится и к опыту по дифракции электронов на двух щелях. Вся совокупность известных экспериментальных фактов может найти объяснение, если принять, что дебройлевская волна каждого отдельного электрона проходит одновременно через оба отверстия, в результате чего и возникает интерференция. Поштучный поток электронов тоже дает интерференцию при длительной экспозиции, т. е. электрон, как и фотон, интерферирует сам с собой.

Поясним, что соотношение неопределенностей действительно вытекает из волновых свойств микрочас­тиц. Пусть поток электронов проходит через узкую щель шириной Dх, расположенную перпендикулярно направлению их движения (рис.77). Так как электроны обладают волновыми свойствами, то при их прохож­дении через щель, размер которой сравним с длиной волны де Бройля электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране (Э), характеризуется главным максимумом, расположен­ным симметрично оси Y, и побочными максимумами по обе стороны от главного (их не рассматриваем, так как основная доля интенсивности приходится на главный максимум).

До прохождения через щель электроны двигались вдоль оси Z, поэтому составляющая импульса р_y =0, так что D р_y =0, а координата y частицы является совершенно неопределенной. В момент прохождения элек­тронов через щель их положение в направлении оси Y определяется с точностью до ширины щели, т. е. с точностью Dy . В этот же момент, вследствие дифракции, электроны отклоняются от первоначального на­правления и будут двигаться в пределах угла 2j (j - угол, соответствующий первому дифракционному минимуму).