Волновая функция. С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля

С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большое число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место. Таким образом, описание состояния микрообъекта и его поведения может быть дано только на основе понятия вероятности.

Необходимость вероятностного подхода к описанию микрообъектов является важнейшей особенностью квантовой теории. В квантовой механике для характеристики состояний объектов в микромире вводится особая функция называемая амплитудой вероятности и обычно обозначаемая греческой буквой «пси»: 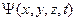. Эту величину называют также волно­вой функцией. Амплитуда вероятности должна быть комплексной, и веро­ятность нахождения частицы в элементе объемом dV равна: .

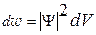Величина 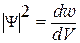(квадрат модуля Ψ-функции) имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестностях точки с координатами x,y,z. Т.о. физический смысл имеет не сама Ψ-функция, а квадрат её модуля |Ψ |², которым задается интенсивность волн де-Бройля.

Полная вероятность w нахождения частицы в конечном объёме V получится, если просуммировать dw по элементам dV, заполняющим этот объём.

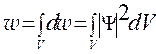(227)

Эта величина должна обращаться в единицу, если за объем V принять бесконечный объём всего пространства. Условие

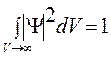(228)

называется нормировочным; оно по­зволяет находить постоянные множи­тели, входящие в Ψ. (Иногда удобно выбирать «нормировочный объём» хотя и большим, но конечным, это помо­гает избежать некоторых формальных трудностей с интегрированием, воз­никающих, например, в случае плоской волны.)

Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий.

Функция Ψ (х, у, z, t)должна быть конечной, (вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной величиной), непрерывной ( вероятность не может изменяться скачком). Производные 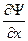, , 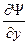, 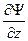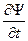должны быть непрерывны; функция |Ψ|² должна быть интегрируема.

Волновая функция Ψ(x,t) играет в квантовой теории первостепенную роль: именно она описывает состояние квантовой системы, поэтому волновую функцию стали также называть век­тором состояния (по ана­логии с тем, как в классической механике положение материальной точки за­даётся с помощью радиуса-вектора). Предложенное Борном толкование волн де Бройля исключает их пони­мание как классических волн материи. Связывая, например, со свободным элект­роном плоскую волну, не нужно понимать это так, будто бы электрон «размазан» по огромной области: в действительности это означает, что хотя электрон продолжает выступать в теории как точечный объект, веро­ятность обнаружить его в любой из точек пространства одинакова.

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Ψ_1, Ψ₂,… Ψ_n, то она также может находиться в состоянии Ψ, описываемом линейной комбинацией этих функций.

,

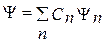где С_n – произвольные, вообще говоря комплексные числа.

Сложение волновых функций (амплитуд вероятностей) и (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема о сложении вероятностей.

Конкретный вид волновой функции определяется внешними условиями, в которых находится микрочастица. Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях. Безграничная монохроматическая волна де Бройля есть волновая функция свободной частицы, на которую не действуют никакие силовые поля.