Уравнение Шредингера для стационарного состояния

Понятие о стационарных состояниях.

У квантовой системы существуют особые состояния, в которых определяемые им вероятности не зависят от времени. Такие состояния называются стационарными. Атомы вещества обычно находятся в стационарных состояниях. Согласно принципу суперпозиции любое нестационарное состояние можно представить как сумму, как наложение друг на друга стационарных состояний.

Для многих физических явлений, происходящих в микромире, временное уравнение Шредингера можно упростить, исключив зависимость y от времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии.

Это возможно, если Ψ -функция удовлетворяет следующим условиям:

1) Потенциальная силовая функция для микрочастицы от времени не зависит:

U(x,t) = U(x) = const

В этом случае U(x) - потенциальная энергия микрочастицы.

2) Ψ - функция со временем не меняться: |Ψ|² = const по времени.

3) Полная энергия остаётся постоянной: E = const по времени.

4) Для стационарных состояний волновая Ψ - функция распадается на 2 сомножителя:

Ψ .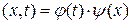

φ(t) - временной сомножитель; ψ(x) - координатная часть истинно волновой функции.

Для нахождения ψ(x,y,z) из (229) и (230) необходимо составить уравнение без времени. Сделаем переход от (229), используя для одномерного случая возможность замены Ψ (x,t) на φ(t) и ψ(x).

; ; ;

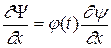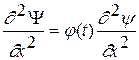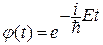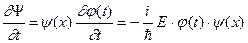
Из (99), поделив обе части уравнения на φ(t), получаем:

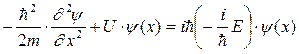
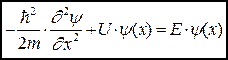(231)

Уравнение (231) - стационарное уравнение Шредингера.

E - полная энергия, U(x) - потенциальная энергия, m – масса, ψ - волновая функция.

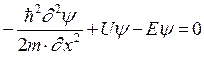
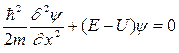
Его можно записать в виде:

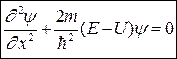(232)

В трехмерном случае

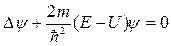, (233)

где Δ - оператор Лапласа.

Уравнения (232) и (233) называются уравнениями Шредингера для стационарных состояний. В эти уравнения в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями y. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называют собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят онепрерывном, илисплошном, спектре, во втором —о дискретном спектре.