Расчет на прочность стержня винта (болта) при различных случаях нагружения

Стержень винта нагружен только внешней растягивающей силой. Примером служит резьбовой участок крюка для подвешивания груза (рис.7.17). Опасным является сечение, ослабленное резьбой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d₁ резьбы.

Условие прочности по напряжениям растяжения в стержне

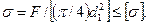(7.21)

Допускаемые напряжения [ ] см. табл.

Болт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин (рис.7.18). В этом случае стержень болта растягивается осевой силой F_зат, возникающей от затяжки болта, и закручивается моментом сил трения в резьбе Т_р , где F равна F_зат.

Напряжение растяжения от силы F_зат

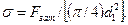
Напряжения кручения от момента Т_р

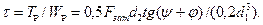(7.22)

Требуемое значение силы затяжки

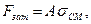
где А —площадь стыка деталей, приходящаяся на один болт, 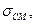— напряжение смятия в стыке деталей, значение которого выбирают по условиям герметичности

Прочность болта определяют по эквивалентному напряжению

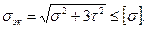(1.23)

Вычисления показывают, что для стандартных метрических резьб

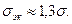
Рассчитывать прочность болтов можно по упрощенной формуле

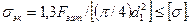(7.24)

Расчетами и практикой установлено, что болты с резьбой меньше М10...М12 можно разрушить при недостаточно квалифицированной затяжке. Например, болт с резьбой М6 разрушается при силе на ключе, равной 45Н; болт с резьбой М12 — при силе 180 Н. В машиностроении не рекомендуют применять болты диаметров меньше М8.

Болтовое соединение нагружено силами, сдвигающими детали в стыке. Условием надежности соединения является отсутствие сдвига деталей в стыке. Конструкция может быть выполнена в двух вариантах.

Болт поставлен с зазором (рис.7.19). При этом внешнюю нагрузку F уравновешивают силами трения в стыке, которые образуются от затяжки болта. Без затяжки болтов детали могут сдвигаться, что недопустимо. Рассматривая равновесие детали 2, получим условие отсутствия сдвига деталей

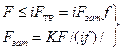, (7.25)

где i—число плоскостей стыка деталей (на рис. 1.19 i=2; при соединении только двух деталей i =1); f—коэффициент трения в стыке (f ≈0,15...0,20 для сухих чугунных и стальных поверхностей); К—коэффициент запаса (К=1,3...1,5 при статической нагрузке, К=1,8... 2 при переменной нагрузке).

Прочность болта оценивают по эквивалентному напряжению.

В соединении, в котором болт поставлен с зазором, внешняя нагрузка не передается на болт. Болт рассчитывают на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают выбором повышенных значений коэффициента запаса.

Болт поставлен без зазора (рис.7.20). Диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности соединения не учитывают силы трения в стыке. Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза

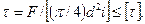(1.26)

где i—число плоскостей среза (на рис.7.20,a i=2; при соединении только двух деталей на рис.7.20,б i=1).

Расчет на смятие производят по условным напряжениям. Эпюру действительного распределения напряжений (рис.7.21,а) заменяют условной с равномерным распределением напряжений (рис.7.21,б). При этом для средней детали (и при соединении только двух деталей)

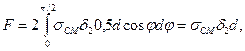
или

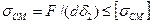
для крайней детали

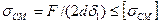
Расчет прочности выполняют по наибольшему напряжению, а допускаемое напряжение определяют по более слабому материалу болта или детали.

Сравнивая варианты установки болтов с зазором и без зазора, следует отметить, что первый вариант дешевле второго, так как не требует точных размеров болта и отверстия. Условия работы болта, поставленного с зазором, хуже, чем без зазора. Например, приняв коэффициент трения в стыке деталей f≈0,2, К=1,5 и i=1, получим F_зат=7,5F. Следовательно, расчетная нагрузка болта с зазором в 7,5 раза превышает внешнюю нагрузку. Вследствие нестабильности коэффициента трения и трудности контроля затяжки работа таких соединений при сдвигающей нагрузке недостаточно надежна.

Болт затянут, внешняя нагрузка раскрывает стык деталей.

Примером служат болты для крепления крышек резервуаров, нагруженных давлением р жидкости или газа (рис.7.22). Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой. Задача о распределении нагрузки между элементами такого соединения статически не определима и решается с учетом деформаций этих элементов. Обозначим: F_зат—сила затяжки болта; F=F 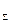/z — внешняя нагрузка соединения, приходящаяся на один болт (z — число болтов).

После приложения внешней нагрузки к затянутому соединению болт дополнительно растянется на некоторую величину ∆, а деформация сжатия деталей уменьшится на ту же величину. Только часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку стыка.

Если обозначим χ коэффициент внешней нагрузки, то дополнительная нагрузка болта равна χF, а уменьшение затяжки стыка — (1—χ)F- Величину коэффициента χ определяют по условию равенства деформаций болта и деталей, возникающих после приложения внешней нагрузки.

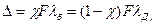(7.28)

где 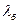—податливость болта, равная его удлинению при единичной нагрузке; 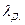—суммарная податливость соединяемых деталей.

Из равенства имеем

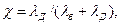(7.29)

Приращение нагрузки на болт

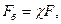(7.30)

Расчетная (суммарная) нагрузка болта

F_p=F_зат+ 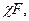(7.31)

и остаточную затяжку стыка от одного болта

F_ст=F_зат –(1-χ)F, (7.32)

На практике рекомендуют принимать

F_зат=K_затF, (7.33)

где К_зат—коэффициент затяжки.

По условию нераскрытия стыка: при постоянной нагрузке K_зат=1,25...2, при переменной нагрузке K_зат=2,5..4.

По условию герметичности: при мягкой прокладке К_зат=1,3...2,5, при металлической фасонной прокладке K_зат=2...3,5, при металлической плоской прокладке K_зат=3...5.

Выбрав значение K_зат при известных 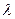_б, 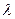_Д или χ, можно определить F_p, F_б и F_ст.

Прочность болта при статических нагрузках. При статических нагрузках прочность болта в соединении типа оценивают по формуле

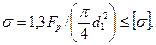(7.34)

Здесь коэффициент 1,3 по-прежнему учитывает напряжения кручения, которые могут возникнуть при затяжке соединения под нагрузкой.

Прочность болта при переменных нагрузках. При переменных нагрузках полное напряжение в болте можно разделить на постоянное

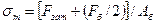
и переменное с амплитудой (7.35)

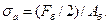
Запас прочности по переменным напряжениям подсчитывают по формуле

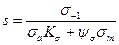(см. табл. 1.2), (7.36)

где 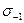—предел выносливости материала болта: 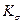—эффективный коэффициент концентрации напряжений в резьбе (определяют при испытании затянутой резьбовой пары); 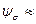0,1—коэффициент чувствительности к асимметрии цикла напряжений.

Значение 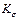зависит от многих факторов и трудно поддается учету. Для приближенных расчетов рекомендуют: 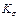≈3,5...4,5—углеродистые стали, 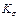≈4...5,5—легированные стали. Большие значения относятся к резьбам d>20 мм. Эти значения получены для метрических нарезных резьб и при простых гайках. Для накатанных резьб 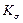уменьшают на 20...30%: При применении специальных гаек, выравнивающих распределение нагрузки по виткам резьбы, значение 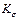уменьшают на 30...40%.

Запас статической прочности по текучести материала проверяют по формуле

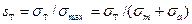(7.37)

Приближенный расчет затянутых болтов при растягивающей внешней нагрузке. В большинстве случаев значение затяжки болтов на практике не контролируют, поэтому смысл точного расчета теряется. Для приближенного расчета принимают χ=0,2...0,3. При этом

F_б=(0,2...0,3)F; (7.38)

F_р=F_зат+(0,2...0,3)F. (7.39)

Значение затяжки F_зат выбирают по выше приведенным рекомендациям.

Прочность болтов при высоких температурах. При высоких температурах в болтовом соединении возникают температурные нагрузки. При температурах свыше 150°С для легких сплавов и 300°С для конструкционных сталей в затянутых соединениях становятся существенными явления релаксации и заедания. Для уменьшения релаксации необходимо повышать упругую податливость деталей соединения, применять материалы с высоким пределом ползучести, например, хромистые и хромоникелевые стали, снижать допускаемые напряжения для болтов.

Для борьбы с заеданием необходимо изготовлять гайки из материалов, обладающих более высоким температурным коэффициентом линейного расширения по сравнению с материалом винта (перлитный чугун, бронза, латунь, жаропрочные стали); применять покрытия—омеднение или хромирование резьбы; применять более крупные резьбы с зазором по среднему диаметру.