Тема 8 валы и оси

На валах и осях размещают вращающиеся детали: зубчатые колеса, шкивы, барабаны и т.п. Вал отличается от оси тем, что передает вращающий момент от одной детали к другой, а ось не передает. Например, на рис. 8.1 момент от полумуфты 3 к шестерне 1 передается валом 2, а на рис. 8.2, где изображен барабан грузоподъемной машины, момент от зубчатого венца передается канату самим барабаном. Вал всегда вращается, а ось может быть вращающейся (рис. 8.2,а) или невращающейся (рис. 8.2,б).

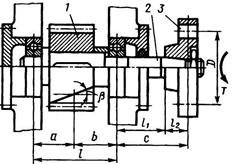
Рис. 8.1 Рис. 8.2

Различают валы прямые, коленчатые и гибкие. Наибольшее распространение имеют прямые валы. Коленчатые валы применяют в поршневых машинах. Гибкие валы допускают передачу вращения при больших перегибах. Коленчатые и гибкие валы относят к специальным деталям и не изучают в настоящем курсе.

По конструкции различают валы и оси гладкие (рис.8.2), фасонные, или ступенчатые (рис.8.1), а также сплошные и полые. Образование ступеней на валу связано с закреплением деталей или самого вала в осевом направлении, а также с возможностью монтажа детали при посадках с натягом. Полыми валы изготовляют для уменьшения массы или в тех случаях, когда через вал пропускают другую деталь, подводят масло и пр.

Прямые валы изготовляют преимущественно из углеродистых и легированных сталей. Чаще других применяют сталь Ст5 для валов без термообработки; сталь 45 или 40Х для валов с термообработкой (улучшение); сталь 20 или 20Х для быстроходных валов на подшипниках скольжения, у которых цапфы цементируют для повышения износостойкости.

Проектный расчет валов.При проектном расчете известны крутящий момент Т или мощность Р и частота вращения п, нагрузка и размеры основных деталей, расположенных на валу. Требуется определить размеры и материал вала.

Валы рассчитывают на прочность, жесткость и колебания. Основной расчетной нагрузкой являются моменты Т и М, вызывающие кручение и изгиб. Влияние сжимающих или растягивающих сил мало и не учитывается. Расчет осей является частным случаем расчета валов при Т=0.

На практике используют следующий порядок проектного расчета вала:

1. Предварительно оценивают средний диаметр вала из расчета только на кручение при пониженных допускаемых напряжениях.

Напряжения кручения

τ=T/W_p=T/(0,2d³)≤[τ] или d= 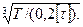(8.1)

принимают:

[τ]=(20...30) МПа для трансмиссионных валов,

[τ]=(12...15) МПа для редукторных валов (8.2)

Диаметр проектируемого вала можно принять, ориентируясь на диаметр вала, с которым он соединяется (валы передают одинаковый момент Т). Например, если вал соединяется с валом электродвигателя, то диаметр его входного конца можно принять равным диаметру выходного конца вала электродвигателя.

2. Далее разрабатывают его конструкцию.

3. Выполняют проверочный расчет выбранной конструкции, и, если необходимо, вносят исправления. Диаметр вала является основным параметром, определяющим размеры и нагрузочную способность подшипников. На практике часто диаметр вала определяется не прочностью самого вала, а прочностью подшипников. Поэтому расчеты вала и подшипников взаимосвязаны.

Проверочный расчет валов.Выбор расчетной схемы и определение расчетных нагрузок.Расчет валов производятся по расчетным схемам. При переходе от конструкции к расчетной схеме производят схематизацию нагрузок, опор и формы вала. В результате схематизации расчет валов становится приближенным.

В расчетных схемах используют три основных типа опор: шарнирно-неподвижную, шарнирно-подвижную, защемление или заделку. Выбирая тип расчетной опоры, необходимо учитывать, что деформативные перемещения валов весьма малы, и если конструкция опоры допускает небольшой поворот или перемещение, то этого достаточно, чтобы считать ее шарнирной или подвижной. При, этих условиях подшипники, одновременно воспринимающие осевые и радиальные нагрузки, заменяют шарнирно-неподвижными опорами, а подшипники, воспринимающие только радиальные нагрузки —шарнирно-подвижными.

Условимся в дальнейшем все рассуждения иллюстрировать примером расчета вала, изображенного на рис.8.1. Для этого вала, учитывая наклон зуба шестерни и направление момента T, левую опору заменяем шарнирно-неподвижной, а правую—шарнирно-подвижной опорами (рис.8.3).

Действительные нагрузки не являются сосредоточенными, они распределены по длине ступицы, ширине подшипника и т.п. Расчетные нагрузки рассматривают обычно как сосредоточенные. В нашем примере (рис.8.1) вал нагружен силами F_t, F_a и F_r, действующими в полюсе зацепления (рис.8.3,а), и крутящим моментом Т на полумуфте. Большинство муфт нагружают вал дополнительной силой F_M. При расчете валов приближенно можно принимать F_м=(0,2...0,5)F_tм, где F_tм — окружная сила муфты. Направление силы F_м в отношении силы F_t зависит от случайных неточностей монтажа. В расчетной схеме (рис,8.3,а) силу F_м направляем так, чтобы она увеличивала напряжения и деформации от силы F_t.

Для стандартных редукторов общего назначения принимают: 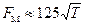- входные и выходные валы одноступенчатых редукторов; 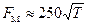- выходные валы многоступенчатых редукторов. Здесь Т—в Н·м.

На рис.8.3,б силы F_t, F_r и F_a приведены к оси вала и изображены раздельно в вертикальной и горизонтальной плоскостях. При этом возникли пары сил, равные T=0,5F_td₁ и Ма=0,5F_ad₁. Здесь d₁ — делительный диаметр шестерни.

Под расчетной схемой построены эпюры изгибающих и крутящих моментов в вертикальной и горизонтальной плоскостях от всех действующих нагрузок (рис.8.3,в,г,д). По этим эпюрам легко определить суммарные изгибающие моменты в любом сечении вала. Например, для сечения I-I изгибающий момент

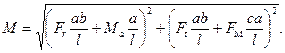
Расчет на прочность. Расчет на сопротивление усталости для валов является основным. Расчет на статическую прочность выполняют как проверочный. При расчете на сопротивление усталости необходимо, прежде всего, установить характер цикла напряжений. В большинстве случаев трудно установить действительный цикл нагрузки машины в условиях эксплуатации Тогда расчет выполняют по номинальной нагрузке, а циклы напряжений принимают—симметричным для напряжений изгиба (рис.8.4,а) и отнулевым для напряжений кручения (рис.8.4,б). Выбор отнулевого цикла для напряжений кручения обосновывают тем, что большинство машин работает с переменным крутящим моментом, а знак момента изменяется только у реверсивных машин. Неточность такого приближенного расчета компенсируют при выборе запасов прочности.

Приступая к расчету, намечают опасные сечения вала, которые подлежат проверке (сечения I-I и II-II, рис.8.3). Учитывают характер эпюр изгибающих и крутящих моментов, ступенчатую форму вала и места концентрации напряжений (рис.8.1). Для опасных сечений определяют запасы сопротивления усталости и сравнивают их с допускаемыми. При совместном действии напряжений кручения и изгиба запас сопротивления усталости определяют по формуле

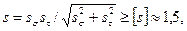(8.3)

где — запас сопротивления

усталости только по изгибу; (8.4)

—запас сопротивления

усталости только по кручению.

В этих формулах σ_а и τ_а — амплитуды переменных составляющих циклов напряжений, а σ_т и τ_т— постоянные составляющие.

Согласно принятому выше условию (рис.8.4), при расчете валов

σ_т=0; σ_а=М/(0,1d³);

τ_т=τ_а=0,5τ=0,5T/(0,2d³); (8.5)

ψ_σ и ψ_τ—коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости.

Значения ψ_σ и ψ_τ зависят от механических характеристик материала.

Принимают:

ψ_σ=0,05; ψ_τ=0-углеродистые мягкие стали;

ψ_σ=0,1; ψ_τ=0,05—среднеуглеродистые стали; (8.6)

ψ_σ=0,15; ψ_τ=0,l—легированные стали;

σ_-1 и τ_-1 —пределы выносливости.

Их определяют по таблицам или приближенным формулам:

σ_-1 ≈(0,4...0,5)σ_в;

τ_-1 ≈(0,2...0,3)σ_в (8.7)

τ_в≈(0,55...0,65)σ_в;

K_d и K_F— масштабный фактор и фактор шероховатости поверхности (рис.8.5 и 8.6); К_σ и К_τ— эффективные коэффициенты концентрации напряжений при изгибе и кручении (ориентировочно можно назначить по табл. 8.1).

Графики рис.8.5 (где 1 - углеродистая сталь при отсутствии концентрации напряжений; 2— легированная сталь при отсутствии концентрации напряжений и углеродистая сталь при умеренной концентрации напряжений К_σ≤2; 3 — легированная сталь при наличии концентрации напряжений) и рис.8.6 (где 1—шлифование тонкое; 2 — обточка чистовая; 3— обдирка; 4 — необработанная поверхность с окалиной и т.п.) позволяют отметить, что с увеличением предела прочности σ_в стали повышается ее чувствительность к резким изменениям формы, влиянию шероховатости поверхности и размеров детали.

Таблица 8.1

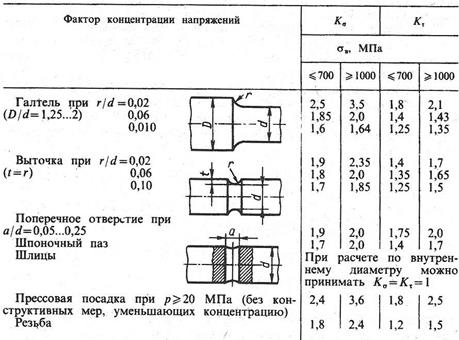
Примечание.При наличии нескольких концентраторов напряжений в одном сечении в расчет принимается тот, у которого больше К_σ или К_τ.

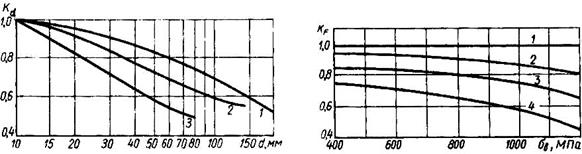
Рис.8.5 Рис.8.6

При разработке конструкции валов из высокопрочных сталей следует уделять внимание уменьшению концентрации напряжений, и шероховатости поверхности.

Сопротивление усталости можно значительно повысить, применив тот или иной метод поверхностного упрочнения: азотирование, поверхностную закалку ТВЧ, дробеструйный наклеп, обкатку роликами. При этом можно получить увеличение предела выносливости до 50% и более. Чувствительность деталей к поверхностному упрочнению уменьшается с увеличением ее размеров.

Проверку статической прочности производят в целях предупреждения пластических деформаций и разрушений с учетом кратковременных перегрузок. При этом определяют эквивалентное напряжение по формуле

σ_эк= 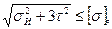(8.8)

где

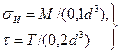(8.9)

Здесь М и Т—изгибающий и крутящий моменты в опасном сечении при перегрузке.

Предельное допускаемое напряжение [σ] принимают близким к пределу текучести σ_т:

[σ]≈0,8 σ_т. (8.10)

Расчет на жесткость. Упругие перемещения вала отрицательно влияют на работу связанных с ним деталей: подшипников, зубчатых колес, катков, фрикционных передач. От прогиба вала (рис. 8.7) в зубчатом зацеплении возникает концентрация нагрузки по длине зуба. При больших углах поворота θ в подшипнике может произойти защемление вала. В металлорежущих станках перемещения валов снижают точность обработки и качество поверхности деталей.

Допускаемые упругие перемещения зависят от конкретных требований к конструкции и определяются в каждом отдельном случае. Для валов зубчатых передач стрела прогиба под колесом [y]≈0,0lm —передачи цилиндрические; [у]≈0,005m—конические, гипоидные, глобоидные передачи, где т - модуль зацепления.

Угол взаимного наклона валов под шестернями γ≈0,001 рад.

В станкостроении для валов общего назначения [y]=(0,0002...0,0003)l

где l—расстояние между опорами.

Угол поворота вала в подшипнике скольжения [θ]=0,001 рад; в радиальном шарикоподшипнике [θ]=0,005 рад.

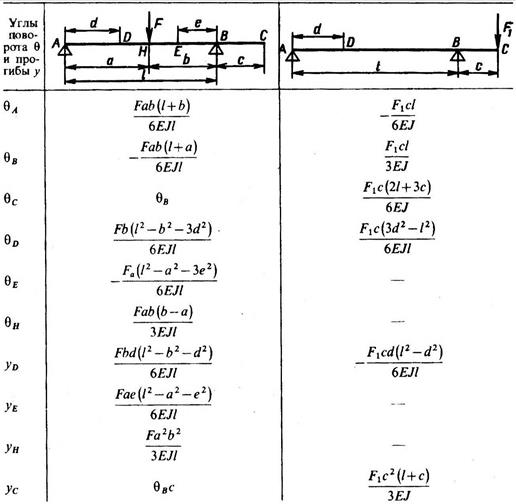
Малое значение допускаемых перемещений иногда приводит к тому, что размеры вала определяет не прочность, а жесткость. В этих случаях нецелесообразно изготовлять вал из дорогих высокопрочных сталей (если это не диктуется какими-либо другими условиями, например износостойкостью цапф). Для простых расчетных случаев можно использовать готовые решения, приведенные в табл. 8.2.

При этом вал рассматривают как имеющий постоянное сечение некоторого приведенного диаметра.

Перемещение при кручении валов постоянного диаметра определяют по формуле

φ=Tl/(GJ_p),

где φ—угол закручивания вала, рад; Т—крутящий момент; G—модуль упругости при сдвиге; l—длина закручиваемого участка вала; J_p=πd⁴/32 — полярный момент инерции сечения вала.

Если вал ступенчатый и нагружен несколькими Т, то угол φ определяют по участкам и затем суммируют.

Расчет на колебания. Вынужденные колебания системы с одной степенью свободы описывает уравнением

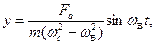(8.11)

где у—амплитуда вынужденных колебаний массы т; F_a— амплитуда возмущающей силы F(t)=F_asinω_вt; ω_в — круговая частота возмущающей силы или частота вынужденных колебаний системы; ω_с — круговая частота свободных колебаний системы.

Таблица 8.2 Формулы для определения углов поворота сечений и прогибов оси двух опорного вала

На вал действует центробежная сила вектор которой вращается с угловой скоростью ω_в.

F_a=m 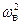e, (8.12)

Составляющие силы F_a по осям у и z:

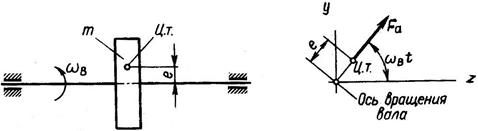
Рис.8.8

F_y=F_asinω_Bt, F₂=F_acosω_Bt. (8.13)

Силы F_y и F_z являются гармоническими возмущающими силами, которые вызывают колебания изгиба вала в направлении осей у и z. Колебания от силы F_y описываются уравнением (8.11), а от силы F_z - аналогичным ему уравнением

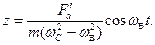
Частота собственных колебаний изгиба

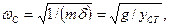(8.14)

где δ=y_cт/(mg) — податливость вала или прогиб от единичной силы; y_cт — статический прогиб вала от действия силы тяжести mg диска.

Уравнение (8.11) позволяет отметить, что при ω_в→ω_с _y→∞. При ω_в=ω_с наступает резонанс. Таким образом, даже при малой неуравновешенности в условиях резонанса можно ожидать разрушения машины.

Частоту вращения (мин^-1), при которой наступает резонанс, называют критической:

n_кр=(30/π)ω_кр=(30/π)ω_c=(30/π) 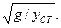(8.15)

Если угловая скорость ω_в больше ω_кр=ω_с, то система при разгоне перейдет зону резонанса и снова стабилизируется. Во избежание поломок зону резонанса следует проходить быстро. Задержки в этой зоне не допускаются.

При ω_в>ω_с амплитуда колебаний меняет свой знак. Установим, что практически это означает.

Полная амплитуда

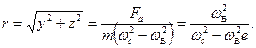(8.16)

Здесь учтено sin²ω_Bt+cos²ω_Bt=l; F_a=m 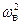e.

При ω_B>ω_с амплитуда r направлена противоположно е и при ω_B>>ω_c r→(- е). Таким образом, за критической зоной центр тяжести несбалансированной массы приближается к геометрической оси вращения. Это явление используют в высокоскоростных механизмах, когда для сохранения устойчивости устанавливают гибкий вал с низкой собственной частотой ω_с. За предел вибрационной устойчивости обычно принимают для жестких валов n≤0,7n_кр, для гибких валов n≥1,3 n_кр.