Тема 11 РЕМЕННЫЕ ПЕРЕДАЧИ
Принцип действия и классификация. Передача состоит (рис.11.1) из двух шкивов, закрепленных на валах, и ремня, охватывающего шкивы. Нагрузка передается силами трения, возникающими между шкивами и ремнем.
По поперечному сечению ремня различают: плоскоременную (рис.11.1,а), клиномеренную (рис.11.1,б) и круглоременную (рис.11.1,в) передачи.
 Преимущества ременной передачи: простота конструкции и эксплуатации; возможность передачи движения на расстояние до 15 м; плавность, бесшумность, возможность работы при высоких скоростях; предохранение механизмов от резких колебаний нагрузки и перегрузки за счет проскальзывания ремня.
Преимущества ременной передачи: простота конструкции и эксплуатации; возможность передачи движения на расстояние до 15 м; плавность, бесшумность, возможность работы при высоких скоростях; предохранение механизмов от резких колебаний нагрузки и перегрузки за счет проскальзывания ремня.
 Недостатки ременной передачи: повышенные габариты; непостоянство передаточного отношения, вызванное проскальзыванием ремня; повышенная нагрузка на валы и их опоры из-за большого предварительным натяжением ремня; низкая долговечность ремней (1000 до 5000 ч).
Недостатки ременной передачи: повышенные габариты; непостоянство передаточного отношения, вызванное проскальзыванием ремня; повышенная нагрузка на валы и их опоры из-за большого предварительным натяжением ремня; низкая долговечность ремней (1000 до 5000 ч).
Мощность передач не превышает 50 кВт. В комбинации с зубчатой передачей ременную передачу устанавливают на быстроходную ступень, как менее нагруженную.
В машиностроении распространены клиновые ремни. Плоские ремни пленочные ремни из пластмасс применяют в высокоскоростных передачах. Круглые ремни - для малых мощностей: в приборах, машинах домашнего обихода.
Основным расчетом ременных передач является расчет по тяговой способности. Долговечность ремня учитывают при расчете путем выбора основных параметров передачи в соответствии с рекомендациями, выработанными практикой.
Кинематические параметры. Окружные скорости на шкивах
vl=nd1nl/60; v2=πd2n2/60. (11.1)
Учитывая упругое скольжение ремня, можно записать v2<v1 или
v2=v1(1-ε), (11.2)
где ε— коэффициент скольжения.
Передаточное отношение
i=nl/n2=vld2/(v2d1)=d2/[dl(1-ε)]. (11.3)
Величина ε зависит от нагрузки, поэтому в ременной передаче передаточное отношение не является строго постоянным. При нормальных рабочих нагрузках до ε≈0,01...0,02. Небольшое значение ε позволяет приближенно принимать
i=d2/dl. (11.4)
Геометрические параметры передачи. На рис. 11.2 а — межосевое расстояние; β —угол между ветвями ремня; α—угол обхвата ремнем малого шкива. При геометрическом расчете известными обычно являются d1, d2 и а, определяют угол α и длину ремня l. Вследствие вытяжки и провисания ремня значения α и l не являются точными и определяются приближенно:
α=180°-β; sin(β/2)=(d2-dl)/(2a).
 Учитывая, что (β/2 не превышает 15°, принимаем значение синуса равным аргументу и запишем
Учитывая, что (β/2 не превышает 15°, принимаем значение синуса равным аргументу и запишем
β≈(d2-d1)/a(рад)≈57(d2-d1)/α°.
При этом

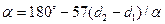
 или (11.5)
или (11.5)
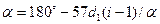
Длина ремня определяется:
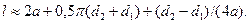 (11.6)
(11.6)
Межосевое расстояние
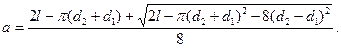 (11.7)
(11.7)
 Силы и силовые зависимости. На рис. 11.3 показано нагружение ветвей ремня в двух случаях: T1=0 (рис.11.3, а) и T1>0 (рис.11.3,б). Здесь обозначено: F0—предварительное натяжение ремня; F1 и F2—натяжение ведущей и ведомой ветвей в нагруженной передаче; Ft=2T1/d1—окружная сила передачи.
Силы и силовые зависимости. На рис. 11.3 показано нагружение ветвей ремня в двух случаях: T1=0 (рис.11.3, а) и T1>0 (рис.11.3,б). Здесь обозначено: F0—предварительное натяжение ремня; F1 и F2—натяжение ведущей и ведомой ветвей в нагруженной передаче; Ft=2T1/d1—окружная сила передачи.
По условию равновесия шкива имеем
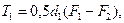
или
 F1-F2=Ft
F1-F2=Ft
Геометрическая длина ремня не зависит от нагрузки и остается неизменной как в ненагруженной, так и в нагруженной передаче. Дополнительная вытяжка ведущей ветви компенсируется равным сокращением ведомой ветви (рис.11.3). Запишем
F1=F0+∆F, F2=F0-∆F,
или
F1+F2=2F0. (11.9)
Из равенств (11.8) и (11.9) следует:
F1=F0+Ft/2, F2=F0-Ft/2. (11.10)
 Получили систему двух уравнений с тремя неизвестными: F0, F1, F2. Эти уравнения устанавливают изменение натяжений ведущей и ведомой ветвей в зависимости от нагрузки Ft, но не вскрывают способности передавать эту нагрузку или тяговой способности передачи, которая связана со значением силы трения между ремнем и шкивом. На рис.11.4 F—натяжение ремня в сечении под углом φ; dR- нормальная реакция шкива на элемент ремня, ограниченный углом dφ; fdR - элементарная сила трения. По условиям равновесия,
Получили систему двух уравнений с тремя неизвестными: F0, F1, F2. Эти уравнения устанавливают изменение натяжений ведущей и ведомой ветвей в зависимости от нагрузки Ft, но не вскрывают способности передавать эту нагрузку или тяговой способности передачи, которая связана со значением силы трения между ремнем и шкивом. На рис.11.4 F—натяжение ремня в сечении под углом φ; dR- нормальная реакция шкива на элемент ремня, ограниченный углом dφ; fdR - элементарная сила трения. По условиям равновесия,
 rF+rfdR-r(F+dF)=0 (сумма моментов)
rF+rfdR-r(F+dF)=0 (сумма моментов)
или fdR=dF;
dR-Fsin(dφ/2)-(F+dF)sin(dφ/2)=0 (сумма проекций). Отбрасывая члены второго порядка малости и принимая sin(dφ/2)≈ dφ>/2, получаем
dR=Fdφ.
Исключая dR, находим
dF/F=fdφ.
Интегрируя, получаем
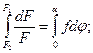
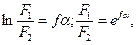
или
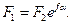 (11.11)
(11.11)
Решая совместно уравнения (11.8) и (11.11) с учетом (11.9), находим:
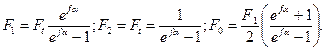 (11.12)
(11.12)
Формулы (11.12) устанавливают связь сил натяжения ветвей работающей передачи с нагрузкой Ft и факторами трения f и α. Они позволяют также определить минимально необходимое предварительное натяжение ремня F0, при котором еще возможна передача заданной нагрузки Fr.
Если
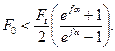
то начнется буксование ремня.
 При круговом движении ремня со скоростью v (рис.11.5) на каждый его элемент с массой dm, расположенный в пределах угла обхвата, действуют элементарные центробежные силы dC. Действие этих сил вызывает дополнительное натяжение Fv во всех сечениях ремня. Элементарная центробежная сила
При круговом движении ремня со скоростью v (рис.11.5) на каждый его элемент с массой dm, расположенный в пределах угла обхвата, действуют элементарные центробежные силы dC. Действие этих сил вызывает дополнительное натяжение Fv во всех сечениях ремня. Элементарная центробежная сила
 dC=(dm)v2/(0,5d)=ρ(dφ0,5dA)v2/(0,5d)=ρAv2dφ,
dC=(dm)v2/(0,5d)=ρ(dφ0,5dA)v2/(0,5d)=ρAv2dφ,
где ρ — плотность материала ремня; А=bδ - площадь поперечного сечения ремня. Из условия равновесия элемента ремня находим
dC=2Fvsin(dφ/2)≈Fvdφ.
Подставляя, находим
Fv=ρAv2. (11.13)
Натяжение Fv ослабляет полезное действие предварительного натяжения F0. Оно уменьшает силу трения и тем самым понижает нагрузочную способность передачи.
Расчеты показывают, что влияние центробежных сил на работоспособность передачи существенно только при больших скоростях: v>20 м/с.
Напряжения в ремне. Наибольшие напряжения создаются в ведущей ветви ремня. Они складываются из σ1, σv, и σи:
σ1=F1/A, σv=Fv/A=ρv2. (11.14)
Учитывая формулу (12.10), напряжение σ1 можно представить в виде
σ1=F0/A+0,5Ft/A=σ0+0,5σt, (11.15)
где
σt=Ft/A (11.16)
— так называемое полезное напряжение; σ0 — напряжение от предварительного натяжения. Полезное напряжение можно представить как разность напряжений ведущей и ведомой ветвей: σt=σl-σ2.
 В той части ремня, которая огибает шкив, возникают напряжения изгиба σи (рис.11.6). По закону Гука,
В той части ремня, которая огибает шкив, возникают напряжения изгиба σи (рис.11.6). По закону Гука,
σи=εE,
 где ε — относительное удлинение, Е—модуль упругости. Значение ε найдем, рассматривая участок дуги ремня, ограниченный углом dφ. Длина нейтральной (средней) линии на этом участке равна (d/2)dφ, а длина наружной линии (d/2+δ/2)dφ.
где ε — относительное удлинение, Е—модуль упругости. Значение ε найдем, рассматривая участок дуги ремня, ограниченный углом dφ. Длина нейтральной (средней) линии на этом участке равна (d/2)dφ, а длина наружной линии (d/2+δ/2)dφ.
Удлинение наружного волокна будет (d/2+δ/2)dφ -(d/2)dφ=(δ/2)dφ. Относительное удлинение
ε=(δ/2)dφ/(d/2) dφ =δ/d и далее
σи=Eδ/d. (11.17)
Основным фактором, определяющим значение напряжений изгиба, является отношение толщины ремня к диаметру шкива. Чем меньше это отношение, тем меньше напряжение изгиба в ремне.
Суммарное максимальное напряжение в ведущей ветви в месте набегания ремня на малый шкив
σmах=σ1+σv+σи=σо+0,5σt+σv+σи. (11.18)
 Эпюра распределения напряжений по длине ремня изображена на рис. 11.7.
Эпюра распределения напряжений по длине ремня изображена на рис. 11.7.
 Влияние отдельных составляющих суммарного напряжения на тяговую способность передачи и долговечность ремня. Тяговая способность передачи характеризуется значением максимально допустимой окружной силы Ft или полезного напряжения σо.
Влияние отдельных составляющих суммарного напряжения на тяговую способность передачи и долговечность ремня. Тяговая способность передачи характеризуется значением максимально допустимой окружной силы Ft или полезного напряжения σо.
Учитывая формулу (11.12), нетрудно убедиться, что допустимое по условию отсутствия буксования σt возрастает с увеличением напряжения от предварительного натяжения σо:
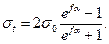 (11.19)
(11.19)
Практика показывает значительное снижение долговечности ремня с увеличением σо. Так, например, для клиновых ремней:
σо, МПа 0,9 1 1,2 1,5 1,8
Относительная долговечность, % 420 250 100 33 13
Поэтому рекомендуют принимать:
Для клиноременных ремней σо≤1,5МПа
Для плоских ремней σо≤1,8МПа
Значение полезного напряжения σt влияет на долговечность примерно так же, как и σо. При указанных значениях σо допустимое значение σt, не превышает 2,0...2,5 МПа.
Оценивая значение напряжений от центробежных сил по формуле (11.14), примем ρ≈1000кг/м3 (для хлопчатобумажных, шерстяных и кожаных ремней ρ≈1000кг/м3, для прорезиненных и клиновых ρ≈1100...1250 кг/м3). Тогда
при v=10м/с σv=0,1 МПа
при v=20м/с σv=0,4 МПа
при v=40м/с σv=1,6 МПа
Для наиболее распространенных на практике среднескоростных (v<20 м/с) и тихоходных (v<10м/с) ременных передач влияние напряжений от центробежных сил несущественно.
Оценивая значения напряжений от изгиба ремня по формуле (11.17), примем среднее значение E=200 МПа (значение Е для различных материалов ремней колеблется в пределах 100...350 МПа). Тогда
при d/δ=200 σи=1 МПа
» d/δ=100 σи=2 МПа
» d/δ= 50 σи=4 МПа
» d/δ=25 σи=8 МПа
Сопоставляя значения различных составляющих суммарного напряжения в ремне и учитывая, что по соображениям компактности в передачах стремятся принимать низкие значения d/δ, можно отметить напряжения изгиба как наибольшие.
В отличие от σо и σt увеличение σи не способствует повышению тяговой способности передачи и являются главной причиной усталостного разрушения ремней.
Результаты испытаний клинового ремня (типа В) при различных диаметрах шкива:
d, мм 160 180 200 225 250 280
Относительная долговечность, % 30 56 100 200 375 600
 Поэтому на практике значение σи ограничивают минимально допускаемыми значениями отношения d/δ.
Поэтому на практике значение σи ограничивают минимально допускаемыми значениями отношения d/δ.
 Долговечность ремня зависит не только от значения напряжений, но также от характера и частоты цикла изменения этих напряжений (рис.11.8).
Долговечность ремня зависит не только от значения напряжений, но также от характера и частоты цикла изменения этих напряжений (рис.11.8).
Частота цикла напряжений равна частоте пробегов ремня:
U=v/l, (11.20)
где v—окружная скорость; l—длина ремня.
Чем больше U, тем меньше долговечность ремня. Поэтому введены ограничения на частоту пробегов ремня:
 для плоских ремней U≤3...5с-1,
для плоских ремней U≤3...5с-1,
» клиновых U≤10...20 с-1 (11.21)
Допускаемые значения U косвенно ограничивают минимальную длину ремня или межосевое расстояние. Рекомендации по выбору межосевых расстояний приведены в формуле (11.25).
Практика эксплуатации позволила установить, что при соблюдении указанных рекомендаций по выбору основных параметров передачи средняя долговечность ремней исчисляется 2000...3000 ч.
Потери в передаче и КПД. Потери мощности в ременной передаче складываются из потерь в опорах валов; потерь от скольжения ремня по шкивам; потерь на внутреннее трение в ремне, связанное с периодическим изменением деформаций, и в основном с деформациями изгиба (рис.11.8): потерь от сопротивления воздуха движению ремня и шкивов.
КПД, передачи определяют экспериментально. При нагрузках, близких к расчетным, среднее значение КПД для плоскоременных передач η≈0,97, для клиноременных η≈0,96.
Допускаемые полезные напряжения в ремне. Определив по кривым скольжения φо, находят полезное допускаемое напряжения для испытуемой передачи:
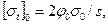 (11.22)
(11.22)
где s≈1,2...1,4—запас тяговой способности по буксованию.
Кривые скольжения получают при испытаниях ремней на типовых стендах при типовых условиях: α=180°, v=10м/с, нагрузка равномерная, передача горизонтальная. Данные заносят в таблицы. Допускаемые полезные напряжения в плоских ремнях [σt]0 (МПа) при σ0=1,8МПа приведены в табл. 11.1.
Таблица 11.1
| Тип ремней | d1,/δ | |||||||||
| Прорезиненные | _ | (2,1) | 2,17 | 2,21 | 2,25 | 2,28 | 2,3 | 2,33 | 2,37 | 2,4 |
| Кожаные | (1,4) | 1,7 | 1,9 | 2,04 | 2,15 | 2,23 | 2,3 | 2,4 | 2,5 | 2,6 |
| Хлопчатобумажные | (1,35) | 1,5 | 1,6 | 1,67 | 1,72 | 1,77 | 1,8 | 1,85 | 1,9 | 1,95 |
| Шерстяные | (1,05) | 1,2 | 1,3 | 1,37 | 1,47 | 1,47 | 1,6 | 1,55 | 1,6 | 1,65 |
Примечания: 1. При σо=2,0 МПа табличные значения [σt]0 следует повышать, а при σо=1,6МПа понижать на 10%. 2. При шкивах из пластмасс и дерева [σt]0 повышают примерно на 20%. 3. При работе в сырых и пыльных помещениях [σt]0 понижают на 16...30%.
Переход от значений [σt]0 для типовой передачи к допускаемым полезным напряжениям [σt] для проектируемой передачи производят с помощью корректирующих коэффициентов:
[σt]=[σt]oCαCv Ср Со, (11.23)
где Cα— коэффициент угла обхвата, учитывающий снижение тяговой способности передачи с уменьшением угла обхвата:
α, град. 150 160 170 180 200 220
Сα 0,91 0,94 0,97 1,0 1,1 1,2
Сv - скоростной коэффициент, вводимый только для передачи без автоматического регулирования натяжения и учитывающий уменьшение прижатия ремня к шкиву под действием центробежных сил:
v, м/с 5 10 15 20 25 30
Сv 1,03 1,00 0,95 0,88 0,79 0,68
Ср — коэффициент режима нагрузки, учитывающий влияние периодических колебаний нагрузки на долговечность ремня.





Ср 1...0,85 0,9...0,8 0,8...0,7 0,7...0,6
С0 — коэффициент, учитывающий способ натяжения ремня и наклон линии центров передачи к горизонту:
Угол наклона линии
центров передачи к горизонту 0...60° 60...80° 80...90°
Передачи с автоматическим
натяжением С0 1 1 1
Передачи с периодическим
подтягиванием С0 1 0,9 0,8
Нагрузка на валы и опоры. Силы натяжения ветвей ремня (за исключением Fv) передаются на валы и опоры (рис.12.15).

Рис.11.14 Рис.11.15
Равнодействующая нагрузка на вал
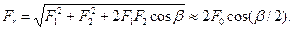 (11.24)
(11.24)
Обычно Fr в 2...3 раза больше окружной силы F, и это, как указывалось выше, относится к недостаткам ременной передачи.
Клиноременная передача.В современных приводах клиноременная передача имеет преимущественное распространение.
 Принципиальные основы конструкции. В этой передаче (рис. 11.1 и 11.17) ремень имеет клиновую форму поперечного сечения и располагается в соответствующих канавках шкива. В передаче может быть один или несколько ремней. Несколько тонких ремней применяют взамен одного толстого для уменьшения напряжения изгиба.
Принципиальные основы конструкции. В этой передаче (рис. 11.1 и 11.17) ремень имеет клиновую форму поперечного сечения и располагается в соответствующих канавках шкива. В передаче может быть один или несколько ремней. Несколько тонких ремней применяют взамен одного толстого для уменьшения напряжения изгиба.
 Форму канавки шкива выполняют так, чтобы между ее основанием и ремнем был зазор ∆. При этом рабочими являются боковые поверхности ремня. В то же время ремень не должен выступать за пределы наружного диаметра dH шкива, так как в этом случае кромки канавок быстро разрушают ремень.
Форму канавки шкива выполняют так, чтобы между ее основанием и ремнем был зазор ∆. При этом рабочими являются боковые поверхности ремня. В то же время ремень не должен выступать за пределы наружного диаметра dH шкива, так как в этом случае кромки канавок быстро разрушают ремень.
Расчетным диаметром dр шкива является диаметр окружности расположения центров тяжести поперечных сечений ремня или нейтрального слоя при изгибе — ширина bр. Все размеры, определяющие форму шкива (H, φ, b1, t, dp, dH), выбирают по соответствующим таблицам стандартов в зависимости от размеров поперечного сечения ремня, которые также стандартизованы.
Применение клинового ремня позволило увеличить тяговую способность передачи путем повышения трения. Положим, что вследствие натяжения ветвей ремня его элемент длиной dl прижимается к шкиву силой dR (рис.11.18).
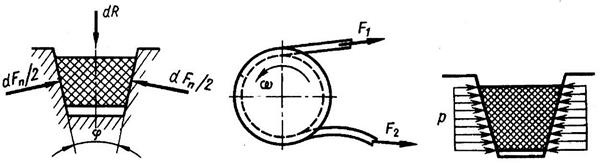
Рис.11.18 Рис.11.19 Рис.11.20
При этом элементарная сила трения, действующая в направлении окружной силы,
dF=dFnf=dRf/sin(φ/2).
В аналогичных условиях для плоскоременной передачи dF=dRf.
Сравнивая эти формулы, можно отметить, что в клиноременной передаче трение увеличивается с уменьшением угла клина φ. Значение
f/sin(φ/2)=f' (11.27)
называют приведенным коэффициентом трения. Для стандартных ремней угол φ принят равным 40°. При этом
f'=f/sin20°≈3f.
Клиновая форма ремня увеличивает его сцепление со шкивом примерно в три раза. Увеличения сцепления путем уменьшения угла φ препятствует появление самозаклинивания ремня в канавках шкива, при котором ремень испытывает дополнительный перегиб на сбегающих ветвях (рис.11.19) и быстрей разрушается от усталости.
Если деформированный ремень, расположить в канавке шкива с углом, равным углу профиля недеформированного ремня, то давление р на его боковые грани распределится неравномерно (рис.11.20). Долговечность ремня в этом случае уменьшится. По стандарту на размеры шкивов клиноременных передач канавки изготовляют с углами 34...40°.
Значительное увеличение трения позволяет сохранить нагрузочную способность клиноременной передачи при значительно меньших углах обхвата по сравнению с плоскоременной передачей. В соответствии с формулами (11.12) при F0=const тяговая способность этих передач (или значение силы Ft) будет оставаться постоянной при условии
αкf'=αпf,
где αк и f'—угол обхвата и коэффициент трения клиноременной передачи; αп и f—то же, для плоскоременной передачи. Имея в виду, что f'≈3f, а по условию (11.25), αп≥150°, получим
αк=αп/3 или αк≥50°.
Для лучшего использования возможностей клиноременной передачи на практике рекомендуется принимать αк≥120° и в редких случаях до 70°. Малое значение допускаемых углов охвата α позволяет строить клиноременные передачи с малыми межосевыми расстояниями а и большими передаточными отношениями i, а также передавать мощность от одного ведущего шкива нескольким ведомым (рис. 11.21).
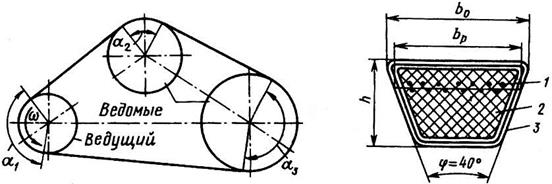
Рис.11.21 Рис.11.22
Конструкция клинового ремня. Применяют ремни с различной структурой поперечного сечения. Одно из типичных и наиболее распространенных сечений изображено на рис. 11.22. Слои шнурового корда 1 являются основным несущим элементом ремня. Они расположены в зоне нейтрального слоя bр для повышения гибкости ремня. Тканевая обертка 3 увеличивает прочность ремня и предохраняет его от износа. Резина 2 как заполнитель объединяет ремень в единое целое и придает ему эластичность.
Клиновые ремни изготовляют в виде замкнутой бесконечной ленты. Для передач общего назначения по ГОСТ 1284.1 — 89 изготовляют семь типов клиновых ремней О, А, Б, В, Г, Д, Е, отличающихся размерами поперечного сечения. Размеры сечения соответственно увеличивают от типа О к Е (табл. 11.2 и рис. 11.17 и 11.22). В табл. 11.2 в качестве примеров приведены параметры только для ремней трех сечений.
Методика расчета передач. Ограниченное число типоразмеров стандартных клиновых ремней позволило определить допускаемую нагрузку для каждого типоразмера ремня, а расчет передачи свести к подбору типа и числа ремней по методике, изложенной в ГОСТ 1284.3—80.
Таблица 11.2
| Сечение ремня | h, мм | b0,мм | bр мм | р,мм | (dp)min., мм | А, м2 | q, кг/м | |
| min | max | |||||||
| О А Б | 10,5 | 8,5 | 47·10-6 81·10-6 138·10-6 | 0,06 0,10 0,18 |
Примечание. А— площадь сечения, q- масса 1 м длины, lp —расчетная длина по нейтральному слою. Ряд длин lp мм: 400, 450, 500, 560, 630, 710, 800, 900, 1000, 1120, 1250, 1400. 1600, 1800, 2000, 2240, 2500, 2800, 3150, 3550, 4000, 4500. 5000, 6000.
 1.Сечение ремня выбирают по графику рис. 11.23, где область применения данного сечения (например, Б) расположена выше собственной линии и ограничена линией предыдущего сечения (например, А).
1.Сечение ремня выбирают по графику рис. 11.23, где область применения данного сечения (например, Б) расположена выше собственной линии и ограничена линией предыдущего сечения (например, А).
 2.По графикам рис.11.24...11.26 определяют номинальную мощность Р0, передаваемую одним ремнем в условиях типовой передачи при α=180°, i=1, спокойной нагрузке, базовой длине ремня, среднем ресурсе. Расчет выполняют по диаметру малого шкива dpl. При выборе диаметров из числа стандартных следует учитывать, что при меньших диаметрах уменьшаются габариты передачи, но увеличивается число ремней.
2.По графикам рис.11.24...11.26 определяют номинальную мощность Р0, передаваемую одним ремнем в условиях типовой передачи при α=180°, i=1, спокойной нагрузке, базовой длине ремня, среднем ресурсе. Расчет выполняют по диаметру малого шкива dpl. При выборе диаметров из числа стандартных следует учитывать, что при меньших диаметрах уменьшаются габариты передачи, но увеличивается число ремней.
Ряд расчетных диаметров dp, мм: 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250, 280, 315, 355, 400, 450, 500, 560, 630, 710, 800, 900, 1000 и далее по ряду Ra40.
3. По формуле (11.28) определяют мощность Рр, передаваемую одним ремнем в условиях эксплуатации рассчитываемой передачи:
Pp=P0CαClCi/Cp, (11.28)
где Сα- коэффициент обхвата [α-по формуле (11.5)]
α, град 180 170 160 150 140 130 120 110 100 90 80 70
Сα 1 0,98 0,95 0,92 0,89 0,86 0,82 0,78 0,73 0,68 0,62 0,56
Cl- коэффициент длины ремня [косвенно учитывает частоту пробегов U- см. формулу (11.20)] по графикам рис. 11.27 (для других сечений см. таблицы ГОСТ 1284.3-80)[lр- по формуле (11.6) с учетом стандартной длины ремня и рекомендаций, приведенных ниже].
Рекомендуемые значения межосевого расстояния а:
i 1 2 3 4 5 6
a 1,5dp2 1,25dp2 dp2 0,95dp2 0,9dp2 0,85dp2
Ci—коэффициент передаточного отношения (рис. 11.28).
Ср—коэффициент режима нагрузки:





Ср 1...1,2 1,1...1,3 1,3...1,5 1,5...1,7
K1 2,5 1,0 0,5 0,25
Выполняя расчет, учитывают следующие рекомендации:
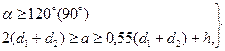 (11.29)
(11.29)
где h—высота поперечного сечения ремня;
z=P/(PpCz), (11.30
где Р—мощность на ведущем валу передачи; Cz - коэффициент числа ремней:
z 1 2...3 4...6 >6
Cz 10,95 0,9 0,85
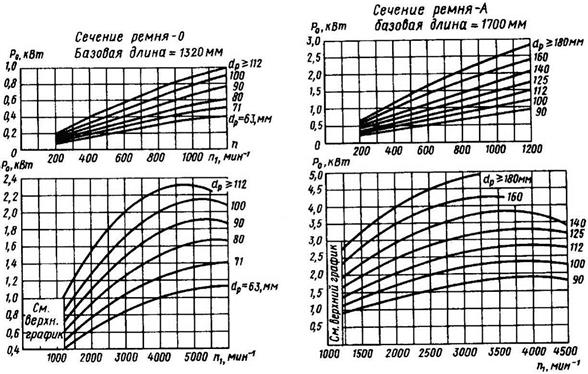
Рис. 11.24 Рис. 11.25
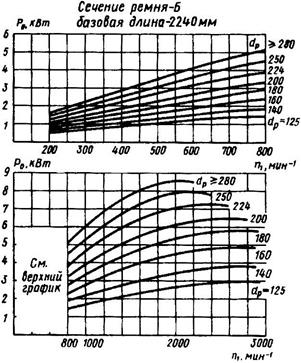
Рис. 11.26
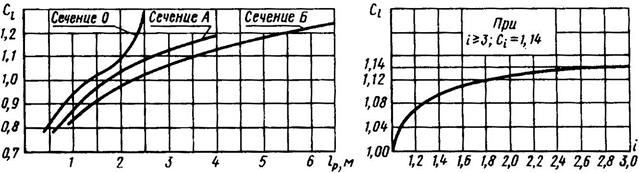
Рис. 11.27 Рис. 11.28
Чем больше число ремней, тем труднее получить их равномерную загрузку. Неизбежные погрешности размеров ремней и канавок шкивов приводят к тому, что ремни натягиваются различно, появляются дополнительные скольжения, износ и потеря мощности. Поэтому рекомендуют
z≤6(8). (11.31)
5. Определяют силу предварительного натяжения одного ремня:
F0=0,85PCpCl/(zvCαCi)+Fv. (11.32)
Первый член формулы (11.32) следует из формулы для коэффициента тяги φ, где без учета корректирующих коэффициентов Ft=P/(zv), а значение коэффициента тяги φ принято равным 0,6. Для передач с автоматическим натяжением (рис. 11.12) Fv=0. При периодическом подтягивании ремня Fv определяют по формуле (12.13), где ρ≈1250 кг/м3; А — по ГОСТу (см.табл. 11.2); v — при расчетной частоте вращения.
6. По формуле (11.24) определяют силу, действующую на вал с учетом числа ремней z и того, что сила Fv нагружает вал только в статическом состоянии передачи.
Ресурс наработки по ГОСТ 1284.2-89 для эксплуатации при среднем режиме нагрузки (умеренные колебания) Tср=2000 ч. При других условиях
T=TcpK1K2, (12.33)
где K1—коэффициент режима нагрузки; K2- коэффициент климатических условий: центральные зоны K2=1, зоны с холодным климатом K2=0,75.
Параметрами оптимизации для клиноременной передачи являются: 1) тип ремня (с учетом числа ремней); 2) диаметры шкивов (с учетом долговечности); 3) межосевое расстояние (с учетом числа пробегов и его влияния на долговечность).
Дата добавления: 2015-07-18; просмотров: 1644;
