Решение. Проверочная матрица позволяет выбрать алгоритм кодирования и декодирования, исходя из того, что единицы в каждой ее строке соответствуют тем символам кодовой

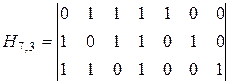. (3.29)

Проверочная матрица позволяет выбрать алгоритм кодирования и декодирования, исходя из того, что единицы в каждой ее строке соответствуют тем символам кодовой комбинации, сумма которых по модулю два должна быть равна 0. Так, из матрицы (3.29) можно получить следующие уравнения проверок:

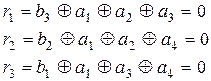(3.30)

Естественно, что (3.27) и (3.30) полностью совпадают с той лишь разницей, что операции по (3.27) выполняются при кодировании для получения значений контрольных разрядов в каждой кодовой комбинации, а операции по (3.30) выполняются при декодировании для обнаружения и исправления ошибок.

Из анализа (3.30) видно, что a₁ входит во все три уравнения, а₂ - в первое и второе, а₃ - в первое и третье, а₄ - во второе и третье. Следовательно, искажение любого а_i нарушит вполне определенные уравнения, т.е. сумма по модулю два в них будет рана не нулю, а единице. По тому, какие именно уравнения нарушены, можно определить, в каком разряде произошла ошибка, и восстановить его истинное значение.

Таким образом, результаты проверок дают кодовую комбинацию вида 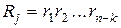, которую называют контрольной последовательностью или, чаще, синдромом. При 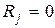считается, что кодовая комбинация принята верно или произошла не обнаруживаемая ошибка. Если 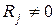, считается, что комбинация принята неверно, т.е. имеет место обнаружение ошибки. Если (n,k)-код используется только для обнаружения ошибок, то в теории кодирования доказывается, что при любой вероятности ошибочного приема кодового символа р£1/2 найдется код, для которого вероятность необнаруженной ошибки будет меньше вполне определенного значения 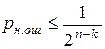. Такие коды называются кодами равномерно обнаруживающими ошибки.

Для исправления ошибок каждому ненулевому синдрому может быть сопоставлен исправляющий вектор E_j , сумма по модулю два которого с принятой кодовой комбинацией образует переданную комбинацию. Пусть, например, передается кодовая комбинация из примера 3.8 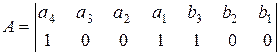, а принимается .

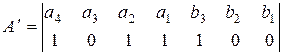При выполнении проверок на приеме в соответствии с системой (3.30) получается

,

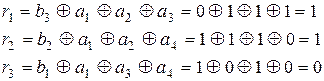т.е. синдром R=110, нарушены первое и второе уравнения, в которые входит а₂, следовательно, ошибка в разряде а₂ и тогда исправляющий вектор Е=0010000, а исправленная кодовая комбинация

.

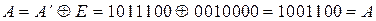Пользуясь этим примером, обратим внимание на третью стоку образующей матрицы (3.26). В части этой строки, соответствующей единичной матрице, единица расположена на месте разряда, в котором произошла ошибка, а получившийся синдром R равен части этой же строки, входящей в дополняющую матрицу.

Обобщая, можно сказать, что при ошибке в разряде а₄ синдром будет 011, при ошибке в разряде а₃ - 101, при ошибке в разряде а₁ - 111.

То же самое следует из проверочной матрицы этого кода (3.29), где первый столбец - синдром при ошибке в разряде а₄ и т.д.

На основании любого из приведенных ранее описаний группового систематического кода (системы проверочных уравнений, образующей матрицы, проверочной матрицы) могут быть синтезированы функциональные схемы кодера и декодера такого кода.

Так, кодер (рис. 3.9) для кода из примера 3.8 должен содержать параллельный регистр, предназначенный для приема от источника и временного хранения четырех информационных разрядов, совокупность из трех трехвходовых сумматоров по модулю два, предназначенных для формирования значений контрольных разрядов, и параллельный семиразрядный регистр для промежуточного хранения сформированной кодовой комбинации, которая далее может быть последовательно передана в линию связи. Соединение входов сумматоров по модулю два с выходами первого регистра выполняются в соответствии с системой проверочных уравнений.

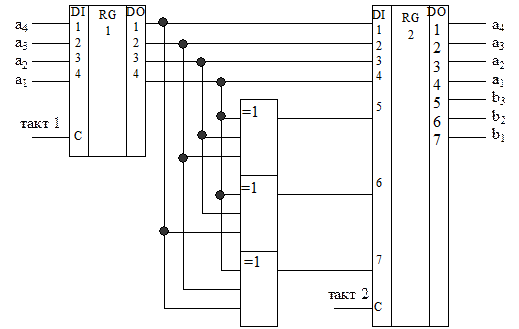
Рис. 3.9

Сложность схемы декодера для такого кода будет зависеть от того, используется ли данный код в режиме обнаружения ошибки или в режиме исправления ошибки.

Для режима исправления ошибки в составе декодера (рис. 3.10) должны присутствовать следующие функциональные узлы:

- регистр для временного хранения принятой кодовой комбинации;

- устройство вычисления синдрома;

- дешифратор синдрома;

- устройство исправления ошибки;

- регистр для хранения исправленной информационной части комбинации.

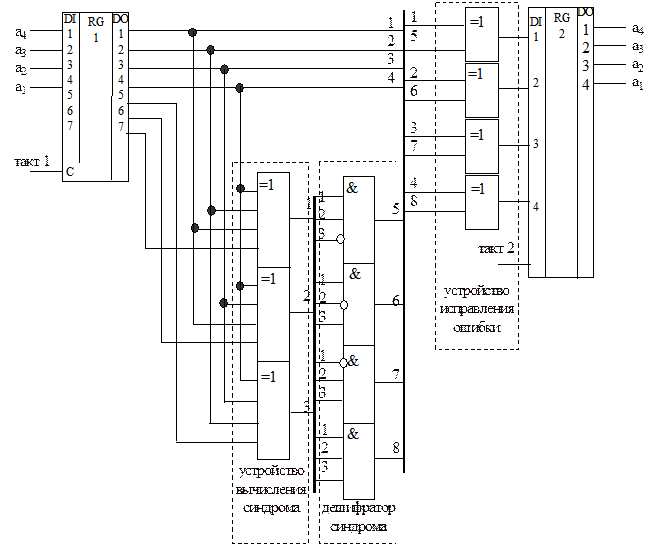
Рис. 3.10

Устройство вычисления синдрома представляет собой совокупность из трех сумматоров по модулю два, каждый из которых имеет по четыре входа, которые соединяются с выходами первого регистра в соответствии с системой проверочных уравнений, а выходы подключены к входам дешифратора синдрома. Дешифратор синдрома осуществляет преобразование синдрома в исправляющий вектор. Устройство исправления ошибок может быть реализовано в виде совокупности из четырех сумматоров по модулю два, каждый из которых имеет по два входа. Первые входы сумматоров соединяются с выходами информационных разрядов первого регистра, а вторые входы подключаются к соответствующим выходам дешифратора синдрома, а выходы соединены с соответствующими входами второго регистра.

Декодер, работающий в режиме обнаружения ошибок, проще, поскольку в нем отсутствует устройство исправления ошибок, а дешифратор синдрома может быть заменен одной схемой выявления ненулевого синдрома (рис. 3.11).

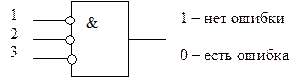
Рис. 3.11

Рассмотренный алгоритм декодирования блоковых групповых линейных систематических (n, k)- кодов, называемый иногда синдромным, относится к классу алгебраических методов декодирования, в основе которых лежит решение системы уравнений, задающих расположение и значение ошибки.

Для декодирования этих кодов могут использоваться и неалгебраические методы, использующие простые структурные понятия теории кодирования, которые позволяют найти комбинации ошибок более прямым путем. Одним из таких алгоритмов является декодирование по максимуму правдоподобия.

Этот метод основывается на том предположении, что если все кодовые комбинации передаются по двоичному симметричному каналу с равной вероятностью, то наилучшим решением при приеме является такое, при котором переданной считается кодовая комбинация, отличающаяся от принятой в наименьшем числе разрядов.

В связи с этим алгоритм максимального правдоподобия реализуется в виде следующей последовательности действий:

1) принятая кодовая комбинация Y суммируется по модулю два последовательно со всеми кодовыми комбинациями кода X_i , в результате каждого суммирования вычисляются векторы ошибок e_i = Y+X_i ,

2) подсчитывается число d_i единиц в каждом из векторов ошибки e_i.

3) та из X_i, для которой d_i минимально, считается переданной кодовой комбинацией.

Для некоторых систематических (n,k)-кодов неравенство (3.23)

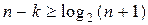
превращается в строгое равенство

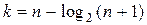. (3.31)

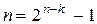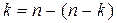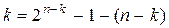Для таких кодов можно записать и, поскольку , то . (n,k)-коды вида 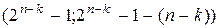называются кодами Хэмминга..

Образующая матрица кода Хэмминга (7,4) приведена ранее (3.26). Образующие матрицы кодов больших размерностей строятся аналогично. Уравнение (3.31) имеет целочисленные решения при k=0,1,4,11,26,57,120, . . , что дает соответствующие коды Хэмминга (3,1), (7,4), (15,11), (31,26), (63,57), (127,120),. . . . Коды Хэмминга относятся к немногим известным т.н. совершенным кодам.

С учетом данных ранее определений кодового пространства и кодового расстояния представим некоторый код в виде сфер с центрами во всех разрешенных кодовых комбинациях. Все сферы имеют одинаковый целочисленный радиус. Будем увеличивать его, оставляя целочисленным, до тех пор, пока сферы не соприкоснутся. Значение этого радиуса равно числу исправляемых кодом ошибок. Этот радиус называется радиусом сферической упаковки кода.

Теперь позволим этому радиусу увеличиваться до тех пор, пока каждая точка кодового пространства не окажется внутри хотя бы одной сферы. Такой радиус называется радиусом покрытия кода. Радиус упаковки и радиус покрытия кода могут совпадать.

Код, для которого сферы некоторого одинакового радиуса вокруг кодовых слов, не пересекаясь, покрывают все кодовое пространство, называются совершенными. Совершенный код удовлетворяет границе Хэмминга с равенством. Код Хэмминга, имеющий длину 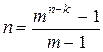, является совершенным.

Код, у которого сферы радиуса t вокруг каждого кодового слова не пересекаются и все кодовые слова, не лежащие внутри какой-либо из этих сфер, находятся на расстоянии t+1 хотя бы от одного кодового слова, называется квазисовершенным. Квазисовершенные коды встречаются чаще, чем совершенные. Если для заданных n и k существует квазисовершенный и не существует совершенного кода, то для этих n и k не существует кода с большим, чем у квазисовершенного, кодовым расстоянием.

Систематические коды, в том числе и код Хэмминга, допускают различные преобразования, которые, порождая новые коды, тем не менее, не выводят их из класса линейных групповых кодов.

К числу наиболее часто используемых преобразований кодов относят укорочение и расширение кодов.

Укорочение кода состоит в уменьшении длины кодовых комбинаций путем удаления лишних информационных разрядов. Если код задан порождающей матрицей, то это приводит к уменьшению обоих размеров порождающей матрицы на одно и то же число. Так, например, как упоминалось ранее, коды Хэмминга с d=3 могут быть построены с вполне определенным сочетанием n и k. Как поступить в том случае, если требуется код Хэмминга с d=3, для передачи информации достаточно k=8, а на длину кодовой комбинации наложено ограничение n<15. Для выполнения этих требований можно выбрать код Хэмминга (15,11) и прибегнуть к его укорочению. Укорочение производится за счет удаления требуемого числа лишних информационных разрядов, обычно это первые слева разряды. В образующей матрице кода (15,11) полагаются равными нулю столько столбцов слева, сколько разрядов надо удалить, после чего вычеркиваются нулевые столбцы и строки с полностью нулевыми строками единичной матрицы. Относительно проверочной матрицы операция укорочения выражается в удалении соответствующего количества первых слева столбцов, так как число строк проверочной матрицы, равное числу контрольных разрядов, остается неизменным при укорочении. Для приведенных значений k=8 и n<15 из кода (15,11) нужно удалить три лишних информационных разряда, в результате чего получится укороченный код (12,8), который также называется кодом Хэмминга.

Расширение кода состоит в увеличении длины кодовых комбинаций за счет введения новых контрольных разрядов, что приводит к увеличению большего размера порождающей матрицы, и, естественно, к увеличению d, т.е. повышению корректирующих способностей. В качестве примера можно привести расширенный код Хэмминга (8,4) с d=4. Этот код образуется путем добавления к каждой кодовой комбинации кода Хэмминга (7,4) еще одного контрольного разряда, значение которого определяется как сумма по модулю два всех остальных разрядов кодовой комбинации, т.е. общая проверка на четность всей кодовой комбинации. При декодировании комбинаций этого кода возможны следующие варианты: 1) ошибок нет. Это показывает как общая проверка на четность, так и равенство нулю синдрома. 2) одиночная ошибка. Общая проверка на четность указывает на наличие ошибки, а по синдрому находится номер искаженного разряда и ошибка в нем исправляется. Нулевой синдром в этом случае указывает на наличие ошибки в дополнительном разряде, т.о. имеет место режим исправления ошибок. 3) две ошибки. Общая проверка на четность указывает на отсутствие ошибок, ненулевой синдром – на их наличие, причем значение синдрома указывает на разряд в котором якобы произошла ошибка, однако в этом случае ее не следует исправлять, а лишь констатировать наличие двух ошибок, т.о. реализуется режим обнаружения ошибок.

Рассмотренные преобразования (укорочение и расширение) можно использовать для модификации известных кодов, чтобы сделать их подходящими для каких-либо конкретных приложений, а также для получения новых классов хороших кодов.