Пространства.
6.6. Любой n-мерный вектор можно единственным образом представить в виде линейной комбинации векторов данного базиса.
Если Е1,Е2, ... ,Еn -образуют базис n-мерного пространства, а
В - любой вектор этого пространства, то можно найти такой единственный набор чиселb1, b2, ..., bn, при которых окажется справедливым равенство
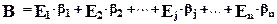 .
.
Это равенство называют разложением вектора В в данном базисе, а числа b1, b2, ..., bn - координатами вектора В в данном базисе.
В матричной форме это равенство можно записать так: 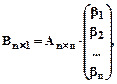
причем столбцы матрицы А можно рассматривать как векторы с координатами в ортонормированном базисе оров Е1,Е2, ... ,Еn.
Векторное n-мерное евклидово пространство имеет бесчисленное множество базисов и любой вектор В этого пространства имеет свои координаты в каждом.
Пример*. Дано: векторы 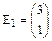 и
и 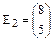 Î R2.
Î R2.
Доказать: Е1 и Е2 образуют базис в пространствеR2.
Доказательство: Базис в R2должен содержать два любых линейно независимых вектора. Векторы будут линейно независимы, если уравнение 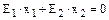 (см. 10.5.) имеет только одно, причем нулевое решение.
(см. 10.5.) имеет только одно, причем нулевое решение.
В матричной форме уравнение имеет вид: 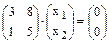 , а в виде системы линейных уравнений его можно записать так:
, а в виде системы линейных уравнений его можно записать так: 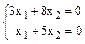 .
.
Для того, чтобы эта система имела единственное решение необходимо и достаточно, чтобы определитель этой системы был не равен нулю (теорема Крамера).
Действительно, 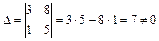 , следовательно Е1 и Е2 - два линейно независимых вектора двумерного пространства и их можно рассматривать как базис этого пространства.
, следовательно Е1 и Е2 - два линейно независимых вектора двумерного пространства и их можно рассматривать как базис этого пространства.
(*) Пусть в n-мерном векторном пространстве задан еще один базис: D1,D2, ...,Dnи связь между старым и новым базисом задана системой векторных уравнений: 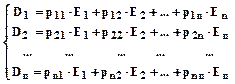
Транспонируем матрицу коэффициентов этой системы обозначим ееР:
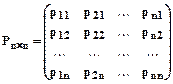 .
.
Матрицу Рназывают матрица перехода от старого базиса (Е1,Е2, ... ,Еn)к новому базису(D1,D2, ... ,Dn). При этом следует обратить внимание на то, что коэффициенты разложения i-го базисного вектора образуют i-й столбец матрицыР.
ЕслиE - матрица из старых базисных векторов, расположенных столбцами, а D- матрица из новых базисных векторов, расположенных столбцами, то связь между старым и новым базисом можно записать в виде матричных уравнений:
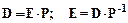 .
.
Пример **. Рассмотрим векторы D1=-2E1+E2 и D2=3E1-2E2 ,
где E1 и E2 - векторы из примера *.
Из условия следует, что 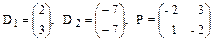 .
.
Векторы D1 и D2 тоже образуют базис R2 (доказательство аналогично примеру *).
Легко проверить, что 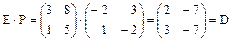 .
. 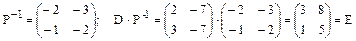 .
.
Пусть дан n-мерный векторХ, который в старом базисе задан координатами xi, а в новом базисе координатами 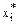 , i=1, 2, ..., n, при этом Р- матрица перехода от старого базиса к новому.
, i=1, 2, ..., n, при этом Р- матрица перехода от старого базиса к новому.
При таких обозначениях связь между координатами вектора Хв старом и новом базисах можно задать равенствами:
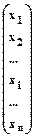 =
= 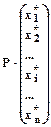 ;
; 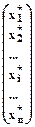 =
= 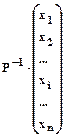 .
.
Из всех возможных базисов чаще всего используются ортогональный базис и ортонормированный базис.
Ортогональным базисом называют базис, все векторы которого попарно ортогональны (скалярное произведение любой пары базисных векторов равно нулю).
Ортонормированным базисом называют такой ортогональный базис, все векторы которого имеют единичную длину.
Если вектор имеет одну координату =1, а остальные его координаты =0, то такой вектор называют орт. Очевидно, что количество всех ортов пространства равно его размерности. Все орты пространства образуют его ортонормированный базис.
Например, в трехмерном пространстве ортонормированный базис образуют орты 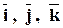 и разложение вектора с координатами 2, 3, 5 в этом базисе можно записать в виде:
и разложение вектора с координатами 2, 3, 5 в этом базисе можно записать в виде: 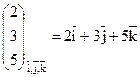 .
.
На координатной плоскости (в векторном пространстве R2 ) ортонормированный базис образуют два орта координатных осей.
Можно проверить, что векторы 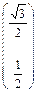 и
и  тоже образуют ортонормированный базис этого пространства.
тоже образуют ортонормированный базис этого пространства.
Если матрица Рортогональная, то ее столбцы можно рассматривать как попарно ортогональные векторы единичной длины (см. пример из 6.2.2.). Следовательно столбцы ортогональной матрицы можно рассматривать как ортонормированный базис пространства соответствующей размерности.
Дата добавления: 2015-08-26; просмотров: 1051;
