Арифметические основы ЦВМ. Системы счисления
Системой счисления называется метод изображения любых чисел с помощью ограниченного количества цифр. Системы счисления бывают позиционными и непозиционными. В позиционных системах счисления значение каждой цифры числа определяется позицией, которую эта цифра занимает по отношению к запятой. В непозиционных системах счисления это правило не действует. Примером непозиционной системы счисления является римская система счисления. Например, в числах IV, VI, в первом числе 1 имеет значение “-1”, во втором числе “+1”. В дальнейшем будем рассматривать только позиционные системы счисления.
Возьмем какое либо десятичное число, например, 384,5610 и представим его в подробном виде:
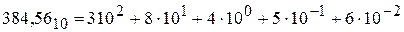
Здесь 3,8,4,5,6 – коэффициенты (цифры) числа, а 102, 101, 100, 10-1, 10-2 – веса соответствующих разрядов, образующие геометрическую прогрессию. Знаменатель прогрессии, т.е. частное от деления веса одного разряда к весу соседнего справа разряда, называется основанием системы счисления. Количество цифр равно основанию. В случае десятичной системы счисления основание 10, в системе 10 цифр: 0,1,2,3….9.
Таким образом любое n-разрядное десятичное число N, имеющее m разрядов в целой части, можно представить в виде :
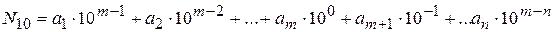 (2.4)
(2.4)
Для приведенного выше числа n=5, m=3, a1=3, a2=8, a3=4, a4=5, a5=6
Наряду с десятичной возможна система счисления с любым основанием в виде целого числа q. В ЦВМ используются двоичная, восьмеричная, шестнадцатеричная системы счисления.
По аналогии с (2.4) любое число N в q-ичной системе счисления можно представить в виде:
Nq=aiqm-1+a2qm-2+…+amq0+am+1q+…+an qm-n, (2.5)
где коэффициенты (цифры) ai, могут принимать целые значения от 0 до q-1, причем количество цифр равно q.
Так, в двоичной системе счисления всего 2 цифры: 0 и 1. Например, 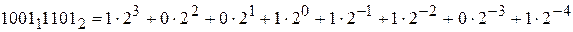 .
.
В восьмеричной системе счисления 8 цифр: 0,1,2…7. Например, 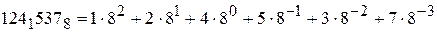
В шестнадцатеричной системе 16 цифр: 0,1,2,…8, 9, A, B, C, D, E, F, где A=10, B=11, C=12, D=13, E=14, F=15. Например, 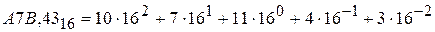
В таблице 2.1 приведены эквиваленты десятичных цифр в различных системах счисления.
| Десятичная цифра | Эквивалент в других системах счисления с основанием | ||||
Табл. 2.1
Дата добавления: 2015-07-14; просмотров: 967;
