Тема. Основні закони та правила алгебри. Дії зі звичайними та десятковими дробами. Формули скороченого множення. Спрощення раціональних виразів.
План
- Числові множини.
- Основні закони та правила алгебри.
- Дії зі звичайними та десятковими дробами.
- Формули скороченого множення.
- Спрощення раціональних виразів.
| 1. Числові множини | ||||||
| Дійсні числа R | ||||||
| Числа, які можна подати у вигляді нескінченного десяткового дробу | ||||||
 
| ||||||
| Раціональні числа Q | Ірраціональні числа | |||||
Можна подати у вигляді нескоротного дробу 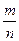 , де m – ціле, n – натуральне число.
Записують у вигляді нескінченного періодичного десяткового дробу , де m – ціле, n – натуральне число.
Записують у вигляді нескінченного періодичного десяткового дробу

| Не можна подати у вигляді нескоротного дробу 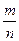 , де m – ціле, n – натуральне число.
Записують у вигляді нескінченного неперіодичного десяткового дробу , де m – ціле, n – натуральне число.
Записують у вигляді нескінченного неперіодичного десяткового дробу
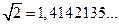
| |||||
 
| ||||||
| Цілі числа Z | Дробові числа | |||||
 Включають натуральні числа, числа, їм протилежні, та число 0 Включають натуральні числа, числа, їм протилежні, та число 0
| Числа , складені із цілого числа часток одиниці 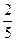 - звичайний дріб,
1,23 – десятковий дріб: 1,23 = - звичайний дріб,
1,23 – десятковий дріб: 1,23 = 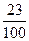
| |||||
| ||||||
| Натуральні числа N (цілі додатні) | Число 0 | Цілі від’ємні числа | ||||
| У шкільному курсі математики натуральне число – основне неозначуване поняття | Таке число, що будь-яке число при додаванні до нього не змінюється а + 0 = 0 + а = а | Числа, протилежні натуральним | ||||
| 2. Основні закони та правила алгебри | ||||||
| Основні арифметичні дії | Властивості | |||||
| Переставна | Сполучна | Розподільна | ||||
| Додавання: a + b = c | a + b = b + a | a + (b + c) = (a + b) + c | - | |||
| Віднімання: a - b = c | a - b = - (b – a) | a - (b - c) = a - b + c (a – b) - c = a - b - c | - | |||
Множення: a  b = c b = c
| a  b = b b = b  a a
| (a  b) b)  c = a c = a  (b (b  c) c)
| (a + b)  c = ac + bc
(a - b) c = ac + bc
(a - b)  c = ac - bc c = ac - bc
| |||
| Ділення: a : b = c | 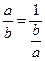
| Ділення числа на добуток:
c : (ab) =(c : a):b = (c : b): a;
ділення добутку на число:
(ab) : c =(a : c)  b = (b : c) b = (b : c)  a a
| Ділення суми (різниці) на число: 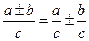
| |||
| Властивості 0 та 1 | |
a + 0 = a; a – 0 = a;
0 – a = - a; a + (- a) = 0;
a – a = 0
(a та – а протилежні числа).
а 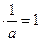 (а та
(а та 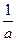 - обернені) - обернені)
| аb = 0, якщо а = 0, або b = 0, або а = b = 0
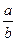 = 0 тільки при а = 0, b = 0 тільки при а = 0, b 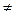 0 0
|
| Вважають, що 0 ділиться на будь-яке число, але ділити на нуль не можна! | |
| 3. Дії зі звичайними та десятковими дробами | |
| Правила | Приклади |
| Основна властивість дробу | |
| Значення дробу не зміниться, якщо чисельник і знаменник дробу помножити або поділити на одне і те саме число (вираз), яке не дорівнює нулю. | 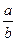 = =  , , 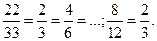
|
| Скоротити дріб – означає поділити чисельник і знаменник дробу на спільний дільник. |  = = 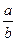 ; ; 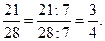
|
| Порівняння дробів | |
| З двох дробів з однаковими знаменниками більший той дріб, чисельник якого більший | 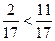 , оскільки 2 < 11 , оскільки 2 < 11
|
| Якщо знаменники різні, то треба дроби звести до спільного знаменника і порівняти їх як дроби з рівними знаменниками. | 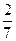 і і 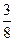 ; ; 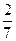 = = 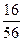 ; ; 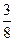 = = 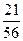 ; ; 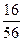 < < 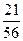 , тобто , тобто 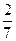 < < 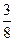 . .
|
| З двох дробів з рівними чисельниками той дріб більший, у якого знаменник менший. | 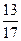 < < 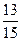 , оскільки 15 < 17. , оскільки 15 < 17.
|
| Додавання і віднімання | |
| Якщо знаменники рівні, то чисельники додаються (віднімаються), а знаменник зберігається. | 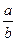 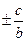 = = 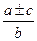
|
| Якщо знаменники різні, то спочатку дроби зводять до спільного знаменника і додають (віднімають) їх як дроби з рівними знаменниками. | 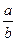 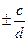 = = 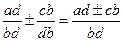
|
| При додаванні (відніманні) мішаних чисел можна додати (відняти) їх цілі і дробові частини. | 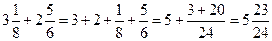
|
| Множення дробів | |
| При множенні дробів помножують чисельники і знаменники | 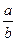  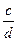 = = 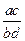
|
| При множенні мішаних чисел їх спочатку перетворюють у неправильні дроби, а потім помножують їх. | 2 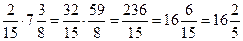
|
| Якщо в добутку один з множників – ціле число, то його подають у вигляді дробу із знаменником 1. | 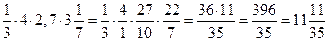
|
| Ділення дробів | |
При діленні двох дробів ділення замінюють множенням першого дробу на обернений другий дріб. 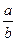 : : 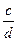 = = 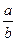  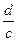 = = 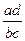
| 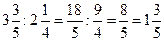
|
| 4. Формули скороченого множення | |
| Квадрат суми | 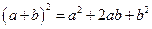
|
| Квадрат різниці | 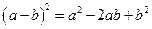
|
| Різниця квадратів | 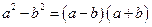
|
| Куб суми | 
|
| Куб різниці | 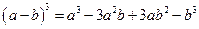
|
| Сума кубів | 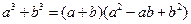
|
| Різниця кубів | 
|
| Пропорції | |
Пропорція – це рівність двох відношень. 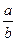 = = 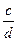 або а : b = c : d (a,b,c,d або а : b = c : d (a,b,c,d 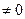 ).
Члени пропорції: a, d – крайні члени, b,с – середні члени. ).
Члени пропорції: a, d – крайні члени, b,с – середні члени.
| |
| Основна властивість пропорції: добуток крайніх членів пропорції дорівнює добутку її середніх членів. ad = bс |
Дата добавления: 2015-08-26; просмотров: 1096;
