За теоремою Гаусса

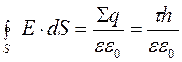. (6.3.14)

Прирівнюємо праві частини (6.3.13) і (6.3.14), одержимо

= .

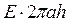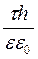Звідки

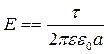, (6.3.15)

що збігається з формулою (6.3.6)

Висновок. Теорема Гаусса значно спрощує розрахунки, але має дуже вузькі рамки використання. Більш загальним, універсальним методом розрахунків напруженості електричного поля є метод суперпозиції, який у кінцевому випадку зводиться до інтегрування.

ЛЕКЦІЯ 7

ПОТЕНЦІАЛ ЕЛЕКТРОСТАТИЧНОГО ПОЛЯ

7.1. Циркуляція вектора напруженості .Теорема про циркуляцію вектора напруженості. Потенціальна енергія заряду.

7.2. Потенціал електростатичного поля. Різниця потенціалів. Принцип суперпозиції.

7.3. Зв’язок між потенціалом і напруженістю електростатич-ного поля . Приклади розрахунку полів.

7.1. Циркуляція вектора напруженості. Теорема про циркуляцію вектора напруженості. Потенціальна енергія заряду

Знайдемо роботу переміщення точкового заряду q_о в електричному полі точкового заряду q із точки 1 в точку 2 (рис 7.1)

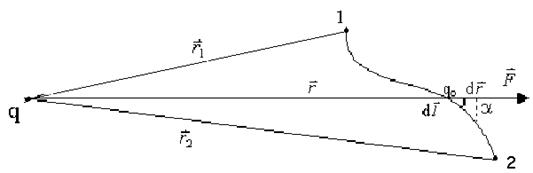
Рис 7.1

На елементарному переміщенні d силою виконується елементарна робота, яка дорівнює

dА = = F·dl·cosa = 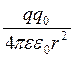dr, (7.1.1)

де dr=dl cos a - проекція переміщення d на напрям дії сили.

Інтегруємо вираз ( 7 .1 .1) в межах від r₁ до r₂ , одержимо

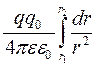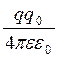
A_1,2 = = 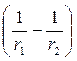. ( 7. 1. 2)

З формули ( 7 .1 .2) видно, що робота переміщення точкового заряду q_о із точки 1 в точку 2 поля статичного заряду q не залежить від форми шляху, а визначається лише положенням початкової й кінцевої точок.

Цей висновок є доказом того, що поле точкового заряду є потенціальним, а діючі в цьому полі сили є консервативними.

У випадку замкнутого контуру робота переміщення точкового заряду q_о в полі статичного заряду q буде дорівнювати нулю (рис 7.2).

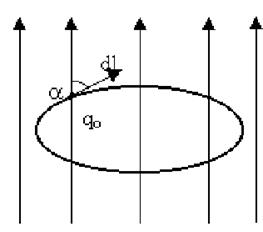
Рис. 7.2

Елементарна робота сил поля на шляху d дорівнює

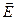q d 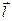= q_oEcosadl = q_oE_edl,

де E_e = Ecosa.

Робота перенесення точкового заряду q_o по замкнутому контуру в цьому випадку буде дорівнювати нулю

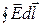q_o = q_o 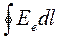=0. ( 7.1 .3)

Оскільки q_o 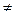0, то

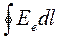= 0. ( 7. 1 .4)

Вираз (7. 1. 4) називають теоремою про циркуляцію вектора 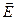електростатичного поля вздовж будь-якого замкнутого контуру.

Силове поле, яке наділене такими властивостями, називають потенціальним полем.

Формула (7.1.4) має використання лише для статичних (нерухомих) зарядів.

В потенціальних полях робота консервативних сил виконується за рахунок зменшення потенціальної енергії.

Скориставшись формулою (7.1.2), виразимо роботу сил поля по переміщенню точкового заряду q_o з точки 1 в точку 2 поля заряду q, через потенціальні енергії заряду q_o, в цих точках ( рис 7 .1)

A_1,2 = 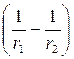= 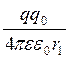- 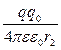= П₁ – П₂, (7.1.5)

де П₁ = 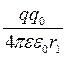- потенціальна енергія заряду q₀ в точці 1 поля точкового заряду q;

П₂ = 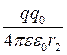- потенціальна енергія заряду q_o в точці 2 поля точкового заряду .

Або виразимо цю роботу через зменшення потенціальної енергії, при перенесенні заряду q₀ з точки 1 в точку 2, тобто

А_1,2 = - ( П₂ – П₁ ) . ( 7. 1. 6)

Якщо поле створюється системою точкових зарядів, то потенціальна енергія заряду q_o, в полі системи точкових зарядів q,_i матиме вигляд

П = q_{o 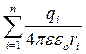.} (7.1 .7)

Важливо знати,що для однойменних зарядів потенціальна енергія їх взаємодії завжди додатна, а потенціальна енергія взаємодії різнойменних зарядів завжди від’ємна.

7.2. Потенціал електростатичного поля. Різниця потенціалів. Принцип суперпозиції

В лекціях з розділу “Механіка“ потенціальна енергія матеріальної точки або тіла визначалась через роботу переміщення тіла з будь-якої точки поля в деяке фіксоване положення, вибране за нульове положення, тобто

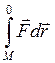= П . ( 7.2.1)

Для електричних зарядів сила 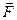= q_o 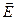, тому

q_o 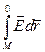= П . ( 7.2.2.)

З рівності (7.2.2) можна зробити висновок, що відношення = const, тобто який би заряд q_i не розміщувати в поле іншого заряду, відношення потенціальної енергії заряду q_i до величини цього заряду для даної точки поля буде величиною сталою. Цю величину називають потенціалом і позначають буквою j , тобто

j = 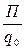. (7. 2. 3)

Потенціал j в будь-якій точці електростатичного поля є скалярною величиною, яка визначається потенціальною енергією позитивного пробного заряду, поміщеного в цю точку.

З урахуванням формули (7 .1. 5) потенціал поля точкового заряду q буде дорівнювати

j = 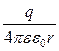. ( 7. 2. 4 )

При переміщенні одиничного позитивного заряду з точки 1 поля в точку 2 виконану роботу можна виразити спочатку через різницю потенціальних енергій, а потім і через різницю потенціалів поля в цих точках, тобто

A_1,2 = П₁ – П₂ = q_o (j₁ - j₂) =q_o Dj. ( 7. 2. 5 )

Різниця потенціалів в двох точках поля j₁ - j₂ визначається роботою сил поля по переміщенню точкового позитивного заряду із точки 1 в точку 2, тобто

j₁ - j₂ = 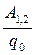. ( 7. 2. 6 )

Якщо вибрати точку 2 за межами поля, скажемо на безмежності, то й потенціал поля там буде дорівнювати нулю. Тому потенціал поля точкового заряду з цих міркувань можна виразити ще й так:

j = 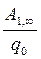, ( 7. 2. 7 )

де A_1,¥ - робота переміщення заряду q_o з даної точки 1 в безмежність; q_o - точковий позитивний заряд.

Потенціал точкового заряду, так само як і різниця потенціалів, вимірюється в Дж/Кл або вольтах ( В ).

Для системи точкових зарядів потенціал поля в довільний точці поля цих зарядів визначається за допомогою принципу суперпозиції полів, тобто

j = 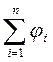, ( 7. 2. 8)

де j_I – потенціал і -го заряду в цій точці поля.

Потенціал поля системи електричних зарядів дорівнює алгебраїчній сумі потенціалів полів всіх цих зарядів. У випадку просторового розміщення системи електричних зарядів, потенціал поля цих зарядів знаходиться шляхом інтегрування.

Розглянемо приклад розрахунку потенціалу просторово розміщених електричних зарядів. Для цього знайдемо потенціал поля рівномірно зарядженого стрижня довжиною l з лінійною густиною зарядів t, в точці А, яка перебуває на продовженні осі стрижня на відстані а від його кінця (рис. 7.3).

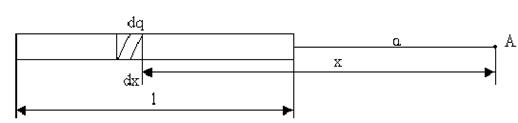
Рис 7.3

На стрижні виділимо безмежно малу ділянку, довжиною dx із зарядом dq, для якої потенціал в точці А можна записати, як для точкового заряду, а саме

dj = 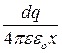. (7.2.9)

Величина точкового заряду dq дорівнює tdx, тому

dj = 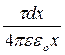. (7.2.10)

Проінтегруємо цей вираз в межах зміни x від а до a+l, тобто

j = 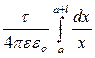= 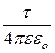ln .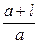

Аналогічно можна виконувати розрахунки потенціалу просторово розміщених електричних зарядів та в інших випадках

7.3. Зв’язок між потенціалом і напруженістю електростатич-ного поля. Приклади розрахунку полів

Як уже показано вище, робота переміщення одиничного позитивного заряду q_o в полі заряду q, виконується за рахунок зменшення потенціальної енергії, тобто

А_1,2 = П₁ – П₂ = -(П₂ – П₁) = -q(j₂ - j₁).

Запишемо цю роботу для безмежно малого переміщення, на якому електричний потенціал змінюється на безмежно малу величину

dА = -q_odj,

і

dА = q_o 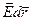. (7.3.1)

Прирівняємо праві сторони рівностей (7.3.1), одержимо зв’язок між потенціалом і напруженістю електростатичного поля:

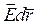= -dj,

звідки

E = - 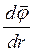. (7.3.2)

Сам потенціал dj є величиною скалярною, а градієнт зміни потенціалу в певному напрямі є величиною векторною.

В більш загальному випадку просторового переміщення точкового заряду формула (7.3.2) набуває вигляду

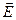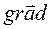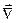= - j = - j,

де 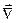- вектор, який має назву оператора Гамільтона або його ще називають “набла”.

Оператор 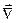є вектором, який також можна записати так

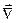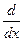
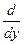
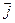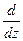
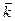= + + , (7.3.3)

де , , 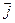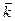- одиничні вектори в напрямку осей x,y,z декартової системи координат.

Знайдемо різницю потенціалів j₂ - j₁, в двох точках поля біля безмежної поверхні з поверхневою густиною зарядів s у відповідності з рисунком (рис.7.4)

Рис 7.4

Скористаємося формулою (7.3.2) зв’язку напруженості електрич-ного поля з потенціалом, одержимо

dj = -Edr. (7.3.4)

Напруженість поля E біля безмежної поверхні розрахована в шостій лекції (6.3.3), тому скористаємось готовим результатом, який дорівнює

E = .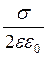

Тоді

dj = - 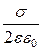dr.

Інтегруємо цей вираз в межах зміни координати від x₁ до x₂ і зміни потенціалу від φ₁ до φ₂, одержимо

= - ,

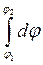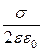
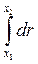звідки

j₂ - j₁ = - 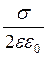(x₂ – x₁),

або

j₁ - j₂ = 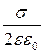(x₂ – x₁). (7.3.5)

2. Потенціали поля в двох точках біля довгого, рівномірно зарядженого стрижня з лінійною густиною зарядів t у відповідності з рисунком (рис. 7.5)

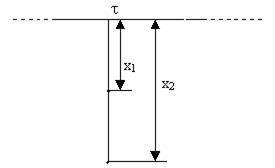
Рис 7.5

На довільній відстані x від стрижня напруженість електричного поля розраховується або за принципом суперпозиції (методом інтегрування), або за теоремою Гаусса. Скористаємось готовою формулою напруженості електричного поля (6.3.15) попередньої лекції

E = .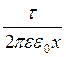

Підставимо це значення напруженості у формулу (7.3.2) та виконаємо інтегрування

dj = - 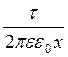dx, (7.3.6)

або

= - ,

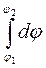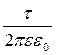
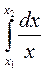звідки

j₁ - j₂ = 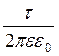ln 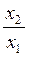. (7.3.7)

Аналогічно можуть бути виконані і будь-які інші розрахунки різниці потенціалів електричного поля статичних зарядів.

ЛЕКЦІЯ 8

ЕЛЕКТРИЧНЕ ПОЛЕ В ПРОВІДНИКУ. ЕЛЕКТРОЄМНІСТЬ

8.1. Провідник в електростатичному полі. Розподіл зарядів у провіднику.

8.2. Електроємність окремого провідника. Конденсатори. Електроємність конденсаторів різної форми.

8.3. Енергія взаємодії електричних зарядів. Енергія окремого провідника й конденсатора.

8.4. Енергія електростатичного поля. Густина енергії електростатичного поля.

8.1. Провідник в електростатичному полі. Розподіл зарядів у провіднику

У металевих провідниках завжди є вільні (не зв’язані з вузлами кристалічної гратки) електричні заряди. Переважно це валентні електрони, які слабо зв’язані з атомами в кристалічній структурі й за цієї причини стали колективізованими. Вільні електрони у провіднику перебувають у неперервному хаотичному русі, рівномірно заповнюючи весь об’єм провідника.

При внесенні такого провідника у зовнішнє електричне поле з сторони останнього на вільні електрони у провіднику, а також на вузли кристалічної гратки, які втративши частину валентних електронів і стали позитивними іонами, будуть діяти електричні сили. Під дією цих сил у провіднику відбувається перерозподіл електричних зарядів. Це призводить до виникнення власного електричного поля, направленого в протилеж-ному напрямку до зовнішнього електричного поля.

Перерозподіл зарядів у провіднику завершиться в той момент, коли внутрішнє поле повністю компенсує зовнішнє електричне поле. Будь-яка зміна величини зовнішнього електричного поля завжди закінчується адекватною зміною величини внутрішнього електричного поля. Так що результуюче поле у провіднику, згідно з принципом суперпозиції, буде дорівнювати нулю. (рис. 8.1).

На рис.8.1 у випадку а) тіло є нейтральним і не таким, у якому відсутні вільні електричні заряди. У випадку б) вільні електричні заряди провідника змістились і утворили власне електричне поле 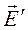, яке зрівноважило або знищило зовнішнє електричне поле 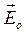. В цьому випадку поле у провіднику буде дорівнювати нулю, тобто

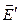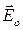+ = 0. (8.1.1)

а) б)

Рис 8.1

Електричне поле 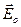провідником деформується. Силові лінії зовнішнього електричного поля входять у провідник перпендикулярно до його поверхні й виходять з провідника теж перпендикулярно до його поверхні.

Поверхня провідника є еквіпотенціальною, тобто поверхнею однакового потенціалу.

Якщо такому провіднику надати додатково електричні заряди величиною q, то і в цьому випадку всередині провідника електричне поле буде відсутнім. Це означає, що і ці електричні заряди електричним полем будуть перерозподілені по поверхні провідника. У провіднику, що перебуває у зовнішньому електричному полі, вільні електричні заряди перерозподіляються лише на його поверхні.

Цю властивість провідників використовують для електростатичного захисту чутливої електронної техніки. Корпуси різних електронних пристроїв виготовляють із провідників. Якщо такий корпус заземлити, то тим самим можна захистити електронні пристрої від будь-яких зовнішніх електричних і магнітних перешкод. Поверхня металевого корпусу стає еквіпотенціальною і добре виконує покладені на неї екрануючі властивості.

Важливо знати:

1. В стаціонарному стані направлений рух вільних зарядів у провіднику відсутній. Електричне поле у провіднику дорівнює нулю. Це означає, що хаотичний рух вільних електричних зарядів у провіднику ніколи не приводить до їх перерозподілу.

2. Якщо внести провідник у зовнішнє електричне поле, то власні вільні електричні заряди, а також додатково передані провіднику вільні електричні заряди за допомогою зовнішнього електричного поля будуть перерозподілятись по поверхні провідника до тих пір, доки своє внутрішнє електричне поле повністю не компенсує зовнішнє електричне поле. При цьому в першу чергу будуть перерозподілені додатково внесені електричні заряди.

3. Оскільки поверхня провідника є еквіпотенціальною, то елек-тричне поле 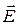, яке дорівнює 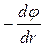, повинно бути перпендикулярним до поверхні в кожній точці провідника.

4. Поле 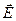на поверхні провідника не дорівнює нулю, однак це поле дорівнює нулю всередині провідника.

8.2. Електроємність окремого провідника. Конденсатори. Ємність конденсаторів різної форми

Надаючи провіднику різні електричні заряди можна виявити, що потенціал провідника при цьому змінюється пропорційно величині заряду, тобто

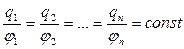. (8.2.1)

Цю сталу величину було названо електричною ємністю провідника. Таким чином, електрична ємність провідника дорівнює

С = 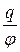, (8.2.2)

де q – заряд провідника, (додатково наданий провіднику); j - потенціал, під яким перебуває його поверхня.

Якщо провіднику був переданий заряд в 1Кл, а його потенціал при цьому змінився на 1В, то ємність такого провідника дорівнює 1Ф (Фарад).

Ємність у 1Ф досить велика. Практично використовують значно менші, кратні значення ємності:

1мкФ = 10^-6 Ф; 1пФ = 10^-12 Ф.

У випадку провідника сферичної форми електрична ємність буде дорівнювати:

С = ,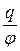

але ,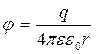

тому

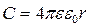. (8.2.3)

Ємність сферичного провідника визначається величиною його радіуса.

Для прикладу знайдемо радіус сферичного провідника, ємність якого буде дорівнювати 1Ф. З формули (8.2.3) маємо

.

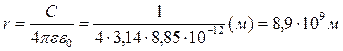Радіус такої кулі перевищує радіус Землі у 1400 разів.

Для практичних цілей ємність окремого провідника використовувати недоцільно через великі розміри. У цьому випадку використовують системи із двох окремих провідників, які називаються конденсаторами. Обидва провідники конденсатора заряджаються рівними за величиною і протилежними за знаком електричними зарядами.

Конденсатори бувають різні. Найбільш широко використовуються плоскі , циліндричні й сферичні конденсатори.

Для кожного типу конденсаторів справедливе співвідношення

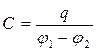, (8.2.4)

де 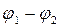- різниця потенціалів між двома окремими провідниками конденсатора; q – заряд кожного знаку на провідниках.

Знайдемо ємності окремих типів конденсаторів.