Лекція 2. Основні поняття квантової механіки
1.2.1. Поняття стану частинки у квантовій механіці. Хвильова функція і її статистичний зміст. Стандартні умови.
1.2.2. Загальне (часове) рівняння Шредінгера.
1.2.3. Рівняння Шредінгера для стаціонарних станів.
1.2.1.Подання стану частинки у квантовій механіці. Хвильова функція і її статистичний зміст. Стандартні умови
У класичній механіці при одновимірному русі вздовж осі х стан частинки в кожний момент часу t задається двома величинами: координатою частинки x(t) і її швидкістю 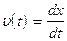 або імпульсом частинки
або імпульсом частинки  . Таке визначення стану частинки є головним вихідним моментом побудови класичної механіки.
. Таке визначення стану частинки є головним вихідним моментом побудови класичної механіки.
В фізиці мікрочастинок через наявність у них хвильових властивостей, класичне визначення стану частинки втрачає будь-який зміст, а з ним і поняття сили, яка за визначенням є функцією класичного стану.
Установити фізичний зміст квантового стану допомогло відкриття корпускулярно-хвильового дуалізму матерії. У квантовій фізиці стан частинки задається хвильовою функцією, яка є комплексною величиною і визначається у всіх точках простору і в будь-який момент часу.
Аналогічно класичним хвилям рух елементарних частинок характеризується хвилями де Бройля. Рівняння хвилі де Бройля елементарної частини називається хвильовою функцією і позначається  . Хвильова функція
. Хвильова функція  не має жодного відношення до механічних хвиль. Класичні хвилі поширюються у пружних середовищах, а елементарні частинки можуть рухатись також і у вакуумі. Слід мати на увазі, що хвилі де Бройля властиві будь-яким частинкам, як зарядженим так і нейтральним, в той час як електромагнетні хвилі випромінюються лише зарядженими частинками при їх прискореному русі.
не має жодного відношення до механічних хвиль. Класичні хвилі поширюються у пружних середовищах, а елементарні частинки можуть рухатись також і у вакуумі. Слід мати на увазі, що хвилі де Бройля властиві будь-яким частинкам, як зарядженим так і нейтральним, в той час як електромагнетні хвилі випромінюються лише зарядженими частинками при їх прискореному русі.
Для класичних хвиль характерні найбільш суттєві властивості, такі як енергія, імпульс, інтенсивність, яка визначається квадратом амплітуди хвилі.
Поняття фізичного змісту хвильової функції прийшло після того, як вияснилось, що в інтерференції хвиль де Бройля проявляються властивості окремих частинок, а не їх системи. Це підтверджується незалежністю інтерференції від інтенсивності частинок в пучку. Інтерференція спостерігається навіть в тих випадках, коли за час польоту від джерела до детектора пролітає лише одна частинка. Цей факт можна тлумачити так лише у випадках, коли рух будь-якої мікрочастинки підпорядковується статистичним закономірностям.
За аналогією з класичними хвилями знайдемо фізичний зміст квадрата модуля хвильової функції
 (1.2.1)
(1.2.1)
де 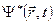 ― функція, комплексно спряжена до
― функція, комплексно спряжена до  .
. 
В досліді Девіссона і Джермера, схема якого показана на рис. 1.1 встановлено, що струм, який реєструється гальванометром, пропорційний квадрату модуля хвильової функції
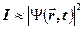 .(1.2.2)
.(1.2.2)
З іншого боку величина цього струму пропорційна також об’єму детектора dV
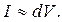 (1.2.3)
(1.2.3)
З урахуванням (1.2.2) і (1.2.3) маємо:
 . (1.2.4)
. (1.2.4)
Якщо імовірність попадання частинок в детектор дорівнює dp, то величина струму гальванометра буде також пропорційною величині цієї імовірності
I = k2dp. (1.2.5)
Прирівнявши рівності (1.2.4) і (1.2.5), одержимо:
 . (1.2.6)
. (1.2.6)
Завжди можна вибрати значення хвильової функції таке, щоб k1=k2.
Тоді (1.2.6) набуде вигляду
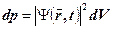 , (1.2.7)
, (1.2.7)
звідки
 . (1.2.8)
. (1.2.8)
Квадрат модуля хвильової функції (1.2.8) визначає густину імовірності виявити частинку в точці з радіусом-вектором 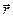 в момент часу t. Квантова механіка на відміну від класичної дає імовірнісне пояснення квантового стану, а хвильова функція має статичний зміст.
в момент часу t. Квантова механіка на відміну від класичної дає імовірнісне пояснення квантового стану, а хвильова функція має статичний зміст.
При відомій хвильовій функції рівність (1.2.8) дозволяє визначити імовірність виявити частинку в об’ємі dV
 . (1.2.9)
. (1.2.9)
Якщо частинка знаходиться у довільній точці простору, то ця подія є достовірною, а імовірність такої події дорівнює одиниці, тобто
 dV =1. (1.2.10)
dV =1. (1.2.10)
Умова (1.2.10) називається умовою нормування.
Як бачимо, квантова механіка має статистичний характер; у ній не ставиться питання про знаходження положення частинки або її траєкторії в просторі, оскільки через хвильові властивості мікрочастинок такі питання взагалі втрачають зміст. У квантовій механіці за допомогою хвильової функції 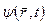 визначається лише імовірність виявлення мікрочастинки в різних точках простору. Зі сказаного випливає, що хвильова функція
визначається лише імовірність виявлення мікрочастинки в різних точках простору. Зі сказаного випливає, що хвильова функція  повинна задовольняти певні обмежувальні умови, які ще називаються стандартними умовами: вона має бути скінченою, однозначною і неперервною, тому що імовірність не може бути більшою за 1; бути неоднозначною і змінюватись стрибкоподібно.
повинна задовольняти певні обмежувальні умови, які ще називаються стандартними умовами: вона має бути скінченою, однозначною і неперервною, тому що імовірність не може бути більшою за 1; бути неоднозначною і змінюватись стрибкоподібно.
Дата добавления: 2015-08-26; просмотров: 932;
