Співвідношення невизначеностей. Межі використання законів класичної фізики
Миттєві стани мікрочастинки не можна характеризувати точними значеннями її координати і імпульсу. Причина в тому, що поведінка мікрочастинок носить імовірнісний характер, що проявляється в наявності в таких частинок хвильових властивостей. Безглуздо говорити про довжину хвилі в даній точці (точка не має розмірів), а оскільки імпульс частинки виражається через довжину хвилі, то звідси випливає, що частинка з визначеною координатою має зовсім невизначений імпульс!
В мікросвіті частинки проявляють при одних умовах хвильові властивості, при інших умовах ― корпускулярні. Якщо виходити лише з корпускулярних властивостей, то згідно з теорією Н. Бора можна визначити точне значення координати частинки в просторі. У випадку хвильових властивостей елементарних частинок поняття координати хвилі немає фізичного змісту.
У класичній механіці траєкторія руху тіла характеризується точними значеннями координати x(t) і імпульсу p(t) в довільний момент часуt, причому ці два параметри, пов’язані між собою. Наприклад, рівномірний і прямолінійний рух тіла масою m із швидкістюu виражається координатою у = ut і імпульсом p(t)=mu, звідки одержуємо, що х(t)= p(t)ּt /m.
У квантовій фізиці з урахуванням хвильових властивостей частинок показано, що у частинки не існує одночасно точних значень координат і імпульсу і що ці величини між собою навіть не пов’язані. Якщо імпульс частинки має точне значення, то її місце знаходження невизначене і навпаки.
Як же характеризувати стан мікрочастинок?
Одним з основних положень квантової механіки є співвідношення невизначеностей, яке було сформульовано в 1927 р. В. Гейзенбергом і з'явилося важливим кроком в інтерпретації закономірностей мікросвіту.
Розглянемо дифракцію електронів на одній щілині. Нехай пучок електронів із швидкістю uлетить в напрямі осі OY так, як це показано на рис. 1.4.
Екран АВ із щілиною шириною d розміщено перпендикулярно до пучка. На другому екраніСД одержано розподіл інтенсивності, який збігається з розподілом інтенсивності при дифракції світла від однієї щілини.
На рис. 1.4 цей розподіл зображено пунктирною лінією. Максимум нульового порядку одержано з кутом дифракції j, який задовольняє умову:
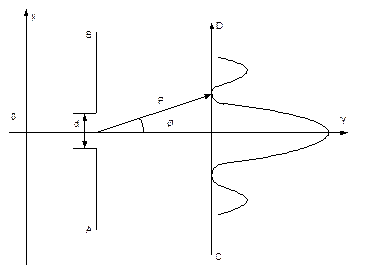
Рис. 1.4
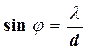 , (1.1.12)
, (1.1.12)
де l ― довжина хвилі, яка відповідає пучку електронів.
З рис. 1.4 видно, що переважна більшість електронів формують нульовий максимум, тому вторинними максимумами в цьому випадку можна знехтувати. Якщо уявити електрони у вигляді механічних частинок, то можна стверджувати, що при їх русі із швидкістю u у напрямі осі OX їх положення визначається з точністю до ширини щілини, тобто
 (1.1.13)
(1.1.13)
В той же час, унаслідок дифракції змінюється напрям швидкості частинок. Враховуючи лише ті електрони, які формують центральний максимум дифракції, похибку у визначенні проекції імпульсу на напрям осі OX знайдемо із умови
 . (1.1.14)
. (1.1.14)
Дата добавления: 2015-08-26; просмотров: 781;
