Класичне означення ймовірності

Імовірність події А дорівнює відношенню кількості елементарних наслідків, сприятливих цій події, до кількості всіх рівноможливих елементарних наслідків у даному випробуванні.

Імовірність події А позначають Р(А), тому за означенням

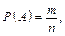
(1)

де m — кількість елементарних наслідків, сприятливих події А; n — кількість усіх елементарних наслідків у даному випробуванні. З класичного означення ймовірності випливає, що

,

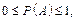причому Р(A) = 0, якщо А = Æ — неможлива подія, і Р(А) = 1, якщо А = W — достовірна подія.

Приклад 2. Знайти ймовірність того, що вибране випадковим чином двозначне число ділиться на: а) 3; б) 5.

Розв’язання. У даному разі випробування полягає в тому, що вибирається випадковим чином двозначне число. Наслідком такого випробування є одне з чисел від 10 до 99. Оскільки таких чисел 90, то n = 90.

а) Нехай подія А = {вибране двозначне число ділиться на 3}. Оскільки кожне третє з 90 двозначних чисел ділиться на 3, то сприятливими для події А є 30 наслідків, тобто m = 30. Тоді за формулою (1) імовірність події А

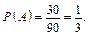
б) Нехай подія В = {вибране двозначне число ділиться на 5}. Загальна кількість наслідків випробування, як і в попередньому випадку, n = 90. Визначимо кількість чисел, які діляться на 5. Очевидно, що таких чисел буде m = 18 (кожне п’яте число ділиться на 5). Отже,

·

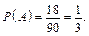Класичне означення ймовірності передбачає, що кількість елементарних наслідків скінченна. Якщо множина всіх елементарних наслідків випробування нескінченна, застосовують геометричне означення ймовірності.