Перетин прямої площиною

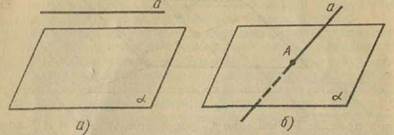
Доведення. Нехай a — дана пряма і α — дана площина (рис. 4). За аксіомою I існує точка А, що не лежить на прямій а. Проведемо через пряму а і точку А площину α'. Якщо площина α' збігається з α, то площина α містить пряму а, що і затверджує теорема. Якщо площина α' відмінна від α, то ці площини перетинаються по прямій а', що містить дві точки прямої а. За аксіомою I пряма а' збігається з а і, отже, пряма а лежить у площині α. Теорема доведена.

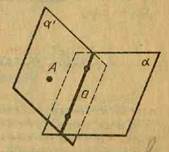
З теореми 1.2 випливає, що площина і пряма, що не лежить на ній, або не перетинаються, або перетинаються в одній точці (рис. 5).

Мал. 4 Мал. 5