Тема. Поняття логарифма числа. Властивості логарифмів
План
1. Логарифм числа.
2. Основна логарифмічна тотожність.
3. Властивості логарифмів.
| 1. Логарифм числа | |
| Визначення | Приклади |
Логарифмом додатного числа b за основою a
(a > 0, 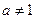 ) називається показник степеня, в який потрібно піднести a, щоб одержати число b.
Позначення: loga b ) називається показник степеня, в який потрібно піднести a, щоб одержати число b.
Позначення: loga b
| 1) log4 16 = 2, оскільки 42 = 16;
2) log7 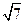 = = 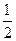 , тому що , тому що 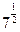 = = 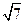 ;
3) lg 1000 = 3, оскільки 103 = 1000 ;
3) lg 1000 = 3, оскільки 103 = 1000
|
| Десятковий логарифм – це логарифм за основою 10. Позначення: log10 b = lg b | |
Натуральний логарифм – це логарифм за основою е (е – ірраціональне число, наближене значення якого: е 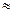 2,7).
Позначення: logе b = ln b 2,7).
Позначення: logе b = ln b
| 4) ln 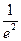 = - 2, тому що е-2 = = - 2, тому що е-2 = 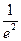
|
| 2. Основна логарифмічна тотожність | |
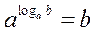 a > 0,
a > 0, 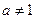 , b > 0 , b > 0
| 1) 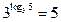 ;
2) ;
2) 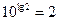 . .
|
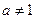 , х > 0, в > 0) , х > 0, в > 0)
| |
1) 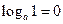
| Логарифм одиниці за будь-якою основою дорівнює нулю |
2) 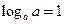
| Логарифм числа a за основою a дорівнює одиниці |
3) 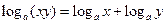
| Логарифм добутку додатних чисел дорівнює сумі логарифмів множників. |
4) 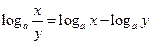
| Логарифм частки додатних чисел дорівнює різниці логарифмів діленого й дільника |
5) 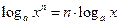
| Логарифм степеня додатного числа дорівнює добутку показника степеня на логарифм основи |
| 4. Формула перехід до логарифмів з іншою підставою | |
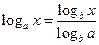 (a > 0,
(a > 0, 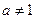 , х > 0, b > 0, , х > 0, b > 0, 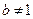 ) )
| |
| Наслідки | |
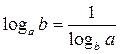
| 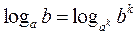
|
Вправи
1.Перевірте, чи вірна рівність:
1) 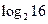 = 4;
= 4;
2) 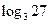 = 3;
= 3;
3) 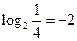 ;
;
4) 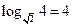 ;
;
5) 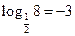 ;
;
6)  = 3.
= 3.
2.Обчислити:
1) 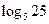 ;
;
2) 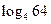 ;
;
3) 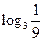 ;
;
4) 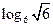 ;
;
5) 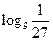 ;
;
6) 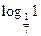 .
.
3. Користуючись основною логарифмічною тотожністю, спростити вираз:
1) 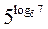 ;
;
2) 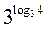 ;
;
3) 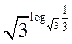 ;
;
4)  ;
;
5) 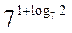 .
.
4. Прологарифмуйте даний вираз за даною основою, якщо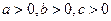 :
:
1) 10a3c4 за основою 10;
2)  за основою 10;
за основою 10;
3)  за основою е;
за основою е;
4) 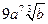 за основою 3.
за основою 3.
5. Відомо, що 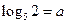 ,
, 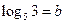 . Виразити через a і b:
. Виразити через a і b:
1) 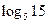 ;
;
2) 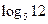 ;
;
3) 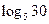 ;
;
4) 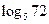 .
.
6. Знайдіть х, якщо:
1) 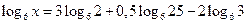 ;
;
2) 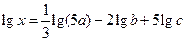 ;
;
3) 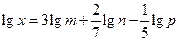 ;
;
4) 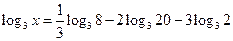 .
.
Дата добавления: 2015-08-26; просмотров: 1950;
