Тема. Показникова функція, її властивості й графік
План
1. Поняття показникової функції.
2. Графік показникової функції.
3. Властивості показникової функції
| 1. Поняття показникової функції | |
Показниковою функцією називається функція виду у = 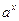 , де , де 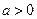 і і 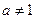 .
Наприклад, у = 2х, у = .
Наприклад, у = 2х, у = 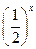 , у = , у = 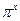 - показникова функція - показникова функція
| |
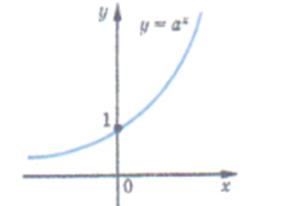
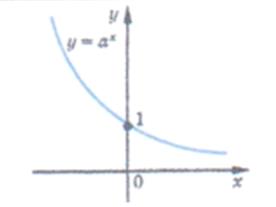
| Графік показникової функції (експонента) | |
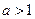
| 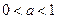
|
| 
|
| 2. Властивості показникової функції | |
1. Область визначення: D(у) = 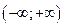
| |
2. Область значень: Е(у) = 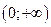
| |
| 3. Функція ні парна, ні непарна | |
| 4. Точки перетинання з осями координат: с віссю Ох – немає з віссю Оу: х = 0, у = 1 | |
| 5. Проміжки зростання й убування: | |
функція у = 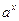 при при 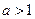 зростає на всій області визначення
зростає на всій області визначення
| функція у = 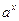 при при 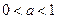 спадає на всій області визначення
спадає на всій області визначення
|
| 6. Проміжки знакосталості: у > 0 при всіх значеннях х | |
| 7. Найбільшого та найменшого значення функція не має | |
8. Для будь-яких дійсних значень u і v (  ) виконуються рівності:
1) ) виконуються рівності:
1) 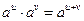 2)
2) 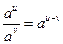 3)
3) 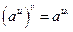 4)
4)  5)
5) 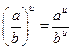
|
Побудуємо графіки показових функцій.
- у =

Складемо таблицю деяких значень функції у =  .
.
| х | - 3 | -2 | -1 | - 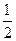
| 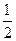
| ||||
| у | 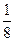
| 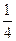
| 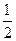
|  0,7 0,7
|  1,4 1,4
|
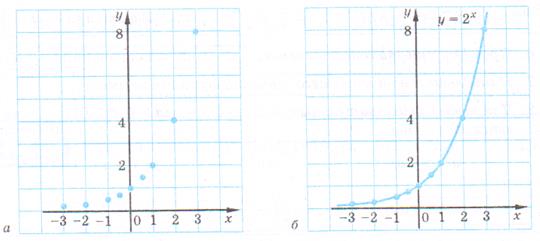
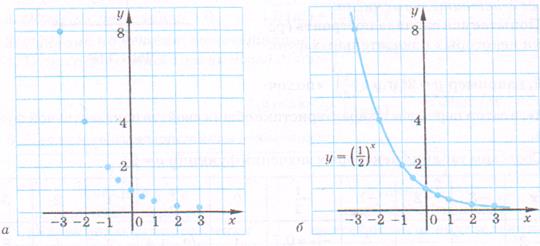
Побудуємо на координатній площині відповідні точки ( мал. 1, а) і з'єднаємо ці точки плавною лінією, яку природно вважати графіком функції у =  ( мал. 1, б).
( мал. 1, б).
- у =
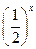
Складемо таблицю деяких значень функції у = 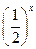 .
.
| х | - 3 | -2 | -1 | - 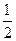
| 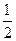
| ||||
| у | 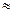 1,4 1,4
| 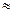 0,7 0,7
| 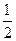
| 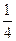
| 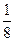
|
Побудуємо на координатній площині відповідні точки ( мал. 2, а) і з'єднаємо ці точки плавною лінією, яку природно вважати графіком функції у = 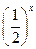 ( мал. 2, б).
( мал. 2, б).
 |
Вправи
- Укажіть, які з даних функцій зростають, які спадають:
1) у = 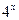 ;
;
2) у = 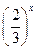 ;
;
3) у = 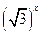 ;
;
4) у = 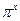 ;
;
5) у = 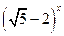 ;
;
6) у = 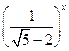 ;
;
7) у = 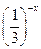 ;
;
8) у = 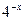 .
.
- Побудуйте графік функції:
1) у = 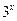 ;
;
2) у = 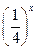 ;
;
3) у = 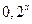 ;
;
4) у = 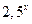 ;
;
5) у = 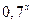 ;
;
6) у = - 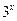 ;
;
7) у = 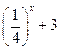 ;
;
8) у = 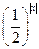 ;
;
9) у = 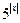 ;
;
10) у = 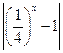 .
.
- Порівняйте значення виразу:
1) 31,5 і 31,4;
2) 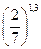 і
і 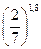 ;
;
3) 0, 78-0,7 і 0, 78-0,6;
4) 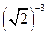 і
і 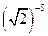 ;
;
5) 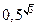 і
і 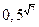 ;
;
6) 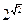 і
і 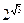 ;
;
7) 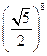 і
і 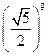 ;
;
8) 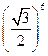 і
і  ;
;
9) 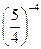 і
і 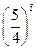 ;
;
10) 0,2-10 і 511.
- Розташуйте числа в порядку їх зростання:
1) 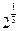 ,
, 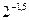 ,
, 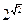 ,
, 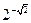 ,
, 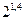 , 1;
, 1;
2) 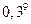 , 1,
, 1, 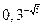 ,
, 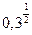 ,
, 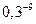 ,
, 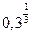 .
.
Дата добавления: 2015-08-26; просмотров: 933;
