Тема. Розв’язання показникових нерівностей
План
1. Графік показникової функції.
2. Схема рівносильних перетворень найпростіших показових нерівностей.
1. Графік показникової функції у = 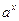 , де , де 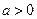 і і 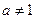 . .
| |
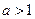
| 
|
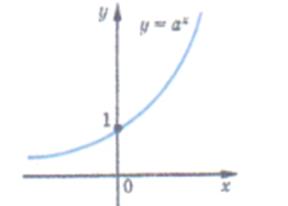 зростає
зростає
| 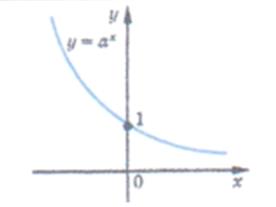 спадає
спадає
|
| 2. Схема рівносильних перетворень найпростіших показових нерівностей | |
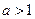
| 
|
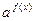 > > 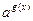 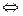 f(x) > g(x)
знак нерівності зберігається f(x) > g(x)
знак нерівності зберігається
| 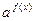 > > 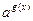 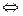 f(x) < g(x)
знак нерівності змінюється на протилежний f(x) < g(x)
знак нерівності змінюється на протилежний
|
| Приклади | |
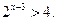
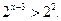 Функція у =
Функція у = 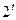 є зростаюча, отже:
х – 3 > 2,
х > 5.
Відповідь: (5; + є зростаюча, отже:
х – 3 > 2,
х > 5.
Відповідь: (5; + 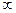 ). ).
| 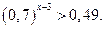
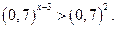 Функція в =
Функція в = 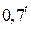 є спадною, отже: є спадною, отже:
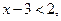
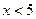 .
Відповідь: (- .
Відповідь: (- 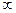 ; 5) ; 5)
|
| 3. Розв’язання більш складних показникових нерівностей | |
| Орієнтир | Приклад |
| За допомогою рівносильних перетворень ( за схемою розв’язання показникових рівнянь) дану нерівність приводять до нерівності відомого виду (квадратному, дробовому і т.д.). Після розв’язання отриманої нерівності приходимо до найпростіших показникових нерівностей | 
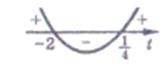 Заміна Заміна 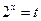 дає нерівність дає нерівність 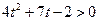 , розв’язання якого , розв’язання якого 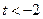 або або 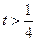 Обернена заміна дає
Обернена заміна дає 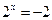 (розв’язаннь немає) або (розв’язаннь немає) або 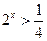 , звідки , звідки 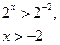 Відповідь: (-2; +
Відповідь: (-2; + 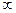 ). ).
|
Вправи
1. Розв'язати нерівність
1) 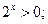
2) 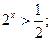
3) 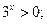
4) 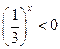 ;
;
5) 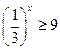 ;
;
6) 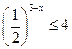 ;
;
7) 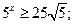
8) 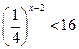 ;
;
9)* 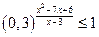 .
.
Дата добавления: 2015-08-26; просмотров: 866;
