Тема. Логарифмічна функція, її властивості й графік
План
1. Логарифмічна функція.
2. Графік логарифмічної функції.
3. Властивості логарифмічної функції.
| 1. Поняття логарифмічної функції | |
Логарифмічною функцією називається функція виду у = loga x, 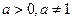 . .
| |
| 2. Графік логарифмічної функції | |
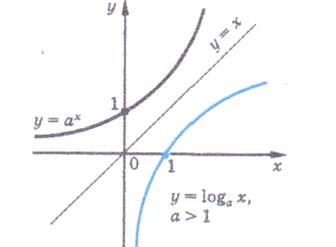
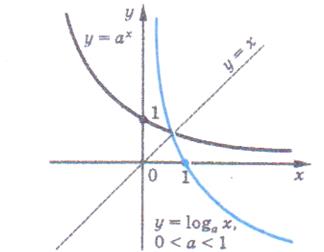
Функції у = 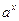 і у = loga x ( і у = loga x ( 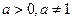 ) – взаємно обернені функції, тому їх графіки симетричні відносно прямою у = х. ) – взаємно обернені функції, тому їх графіки симетричні відносно прямою у = х.
| |
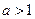
| 
|
| 
|
| 3. Властивості логарифмічної функції | |
1) Область визначення: D(у) = (0; + 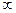 ) )
| |
2) Область значень: Е(у) = (- 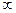 ; + ; + 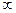 ) )
| |
| 3) Функція ні парна, ні непарна | |
| 4) Точки перетину з осями координат: с віссю Оу – немає з віссю Ох: х = 1, у = 0 | |
| 5) Проміжки зростання та спадання: | |
функція в = loga x при 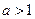 зростає на всій області визначення
зростає на всій області визначення
| функція в = loga x при 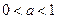 спадає на всій області визначення
спадає на всій області визначення
|
| 6) Проміжки знакосталості | |
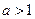
| 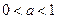
|
| в = loga x > 0 при x > 1, в = loga x < 0 при 0 < x < 1 | в = loga x > 0 при 0 < x < 1, в = loga x < 0 при x > 1 |
| 7) Найбільшого та найменшого значень функціїї не має | |
8) loga a = 1
loga (uv) = loga u + loga v (u > 0, v > 0)
loga 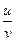 = loga u - loga v (u > 0, v > 0)
loga un = n loga u = loga u - loga v (u > 0, v > 0)
loga un = n loga u
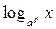 = = 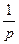 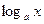
|
Вправи
1. Знайдіть область визначення функції:
1) у = log11 (2х + 6);
2) у = 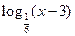 ;
;
3) у = 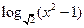 ;
;
4) у = 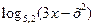 ;
;
5) у = 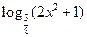 .
.
2. Зобразити схематично графік функції:
1) у = 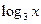 ;
;
2) у = 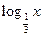 ;
;
3) у = 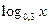 ;
;
4) у = 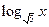 ;
;
5) у =  ;
;
6) у = 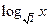 ;
;
7) у = 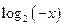 ;
;
8) у = 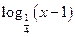 ;
;
9) у = 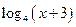 ;
;
10) у = 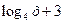 ;
;
11) у = 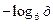 .
.
3. Порівняйте числа:
1)  і
і 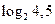 ;
;
2) 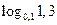 і
і 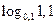 ;
;
3) 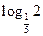 і
і 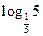 ;
;
4) 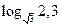 і
і 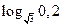 ;
;
5) 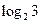 і 0;
і 0;
6) 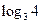 і 1.
і 1.
Дата добавления: 2015-08-26; просмотров: 1211;
