Тема. Розв’язання показникових рівнянь
План
1. Поняття показникового рівняння.
2. Розв’язання показникових рівнянь.
Показникові рівняння – рівняння, в яких невідоме входить тільки до показника степеня.
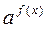 =
= 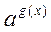
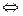 f(x) = g(x), (1)
f(x) = g(x), (1)
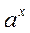 = b, a > 0, a
= b, a > 0, a 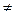 1
1
| 1. Основні формули й співвідношення | ||||
1) 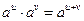 2)
2) 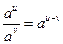 3)
3) 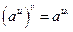
| 4)  5)
5) 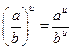 6)
6) 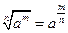
| |||
| 2. Схема рівносильних перетворень найпростіших рівнянь | ||||
| Орієнтир | Приклад | |||
При 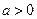 й й 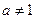
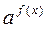 = = 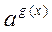 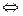 f(x) = g(x) f(x) = g(x)
| 5х = 125; 5х = 53; х = 3. Відповідь: 3 | 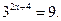
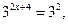
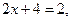
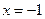 .
Відповідь:
-1. .
Відповідь:
-1.
| 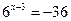 .
Коренів немає, тому що .
Коренів немає, тому що 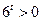 для всіх t.
Відповідь: коренів немає. для всіх t.
Відповідь: коренів немає.
| |
| 3. Приведення деяких показникових рівнянь до найпростіших | ||||
| Орієнтир | Приклад | |||
| 1) Якщо в лівій і правій частинах показникового рівняння стоять тільки добутки, частки, корені або степені, то доцільно за допомогою основних формул спробувати записати обидві частини рівняння як степені з одною основою. | 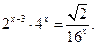
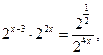
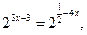 3х - 3 =
3х - 3 = 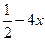 , ,
 .
Відповідь: .
Відповідь: 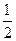 . .
| |||
2) Якщо в одній частині показникового рівняння стоїть число, а в іншій всі члени містять вираз виду 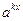 (показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь (показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь 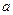 . .
| 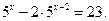
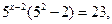
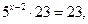
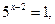
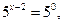
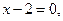
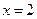 .
Відповідь: 2 .
Відповідь: 2
| |||
Вправи
1. Розв'язати показникові рівняння:
-
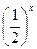 = 2;
= 2; -
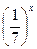 = 49;
= 49;
-
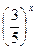 =
= 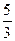 ;
; - 25
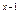 = 1;
= 1; - 3
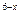 = 3;
= 3; - 0,2
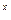 = 0, 008;
= 0, 008; - 0,2
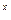 = 125;
= 125; -
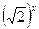 = 8;
= 8; - 2
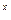 =
= 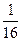 ;
; - 5
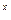 =
= 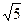 ;
; - 9
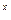 = 3;
= 3; -
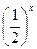 = 4;
= 4; -
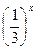 = 27;
= 27; -
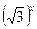 = 3;
= 3; -
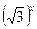 = 1;
= 1; - 81
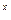 = 3;
= 3; - 2
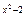 = 4;
= 4; -
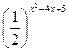 =
= 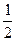 ;
; -
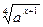 =
= 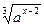 ;
; - 15
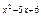 = 1;
= 1; - 2
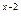 = -2;
= -2; - 5
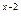 = 125;
= 125; -
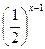 =
= 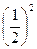 ;
; -
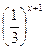 =
= 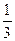 ;
; - 5
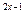 = 5
= 5 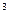 ;
; - 7
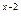 = 7
= 7 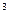 ;
; - 2
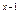 = 4;
= 4; - 0,5
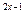 = 0,125;
= 0,125; -
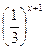 =
= 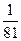 ;
; - 2
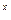 - 2 = 0;
- 2 = 0; - 3
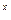 -1 = 0;
-1 = 0; - 3
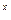
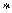 3 = 81;
3 = 81; - 2
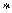 2
2 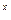 = 32;
= 32; - 3
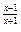 = 9.
= 9.
*2. Розв'язати показникові рівняння:
1. 3х · 52х-3 = 45;
2. 2х · 3х+1 = 108;
3. 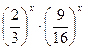 =
=  ;
;
4. 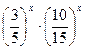 =
= 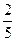 ;
;
5. 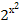 =
= 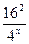 ;
;
-
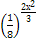 =
= 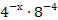 ;
;
7. 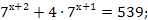
8. 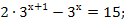
9. 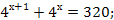
10. 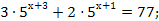
11. 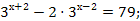
12. 5 · 9 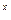 + 9
+ 9 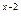 = 406;
= 406;
13. 5 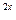 + 4 · 5
+ 4 · 5 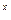 - 5 = 0;
- 5 = 0;
14. 6 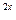 + 5 · 6
+ 5 · 6 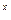 - 6 = 0;
- 6 = 0;
15. 3 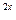 - 2 · 3
- 2 · 3 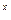 = 3;
= 3;
16. 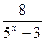 -
- 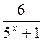 = 3;
= 3;
17. 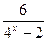 -
- 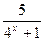 = 2;
= 2;
18. 49 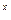 - 6 · 7
- 6 · 7 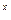 - 7 = 0;
- 7 = 0;
19. 64 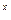 - 7 · 8
- 7 · 8 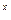 - 8 = 0;
- 8 = 0;
-
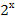 +
+ 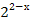 = 5;
= 5; -
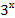 +
+ 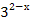 = 10;
= 10; -
 +
+ 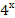 = 80;
= 80; -
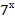 =
= 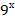 ;
; -
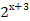 -
- 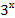 =
= 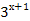 -
- 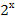
-
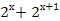 +
+ 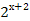 =
= 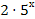 +
+ 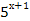 ;
; -
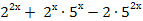 = 0;
= 0; -
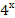 =
= 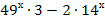 ;
; -
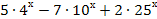 = 0;
= 0; -
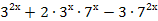 = 0;
= 0; -
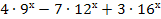 = 0.
= 0.
Дата добавления: 2015-08-26; просмотров: 700;
