Тема. Розв’язання логарифмічних нерівностей
План
1. Графік функції у = loga x, 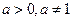 .
.
2. Рівносильні перетворення найпростіших логарифмічних нерівностей.
1. Графік функції у = loga x, 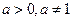 . .
| ||||

| 
| |||
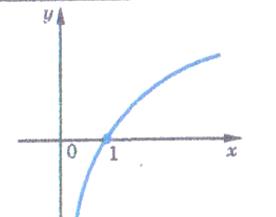 зростає
зростає
|  спадає
спадає
| |||
| 2. Рівносильні перетворення найпростіших логарифмічних нерівностей | ||||

| 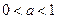
| |||
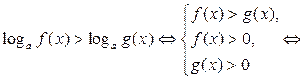
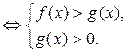 Знак нерівності не змінюється,
і враховується ОДЗ
Знак нерівності не змінюється,
і враховується ОДЗ
|
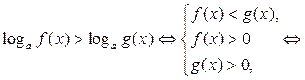
 Знак нерівності змінюється,
і враховується ОДЗ
Знак нерівності змінюється,
і враховується ОДЗ
| |||
| Приклади | ||||
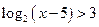 .
ОДЗ: x – 5 > 0, тобто х > 5. .
ОДЗ: x – 5 > 0, тобто х > 5.
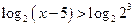 Функція у =
Функція у = 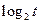 зростаюча, тоді
х - 5 > 23,
х > 13.
Враховуючи ОДЗ, маємо х > 13.
Відповідь: (13; + зростаюча, тоді
х - 5 > 23,
х > 13.
Враховуючи ОДЗ, маємо х > 13.
Відповідь: (13; + 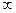 ). ).
| 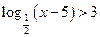 .
ОДЗ: x – 5 > 0, тобто х > 5. .
ОДЗ: x – 5 > 0, тобто х > 5.
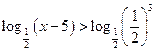 Функція в =
Функція в = 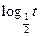 спадна, тоді
х - 5 < спадна, тоді
х - 5 < 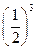 ,
х < 5 ,
х < 5 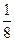 .
Враховуючи ОДЗ, маємо 5 < х < 5 .
Враховуючи ОДЗ, маємо 5 < х < 5 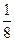 .
Відповідь: (5; 5 .
Відповідь: (5; 5 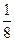 ). ).
| |||
| 3. Розв’язання більш складних логарифмічних нерівностей | ||||
| Орієнтир | Приклад | |||
| І. За допомогою рівносильних перетворень дану нерівність приводять до нерівності відомого виду. Схема рівносильних перетворень нерівності: 1. Ураховуємо ОДЗ заданої нерівності (і уникаємо перетворень, що приходять до звуження ОДЗ). 2. Стежимо за тим, щоб на ОДЗ кожне перетворення можна було виконати як у прямому, так і у зворотному напрямках із збереженням вірної нерівності | 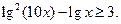 ОДЗ: x > 0. На цій ОДЗ дана нерівність рівносильна нерівностям:
ОДЗ: x > 0. На цій ОДЗ дана нерівність рівносильна нерівностям:
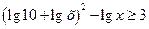 , ,
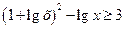 .
Заміна: .
Заміна: 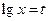 . Тоді . Тоді 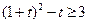 , тобто , тобто 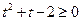 . Рішення цієї нерівності . Рішення цієї нерівності
 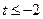 або або 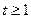 Обернена заміна дає
Обернена заміна дає
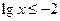 або або  .
Тоді .
Тоді
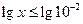 або або 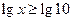 .
Враховуючи, що функція у = lg x є зростаючої, одержуємо: .
Враховуючи, що функція у = lg x є зростаючої, одержуємо:
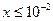 або або 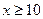 .
За ОДЗ маємо: 0 < x .
За ОДЗ маємо: 0 < x 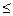 0,01 або 0,01 або 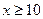 .
Відповідь: .
Відповідь: 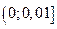 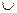 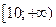 . .
| |||
ІІ. Застосовується загальний метод інтервалів (дана нерівність приводиться до нерівності 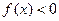 , , 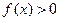 ) і використовується схема:
1. Знайти ОДЗ;
2. Знайти нулі ) і використовується схема:
1. Знайти ОДЗ;
2. Знайти нулі 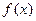 ;
3. Відзначити нулі функції на ОДЗ і знайти знак ;
3. Відзначити нулі функції на ОДЗ і знайти знак 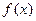 на кожному з проміжків, на які розбивається ОДЗ;
4. Записати відповідь, враховуючи знак нерівності. на кожному з проміжків, на які розбивається ОДЗ;
4. Записати відповідь, враховуючи знак нерівності.
|  Розв'яжемо нерівність методом інтервалів. Воно рівносильне нерівності
Розв'яжемо нерівність методом інтервалів. Воно рівносильне нерівності 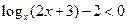 .
Позначимо .
Позначимо 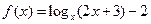 .
1. ОДЗ: .
1. ОДЗ: 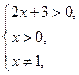 тобто тобто 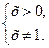 2. Нулі функції:
2. Нулі функції: 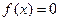 . . 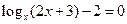 .
Тоді .
Тоді 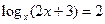 . На ОДЗ це рівняння рівносильне рівнянню 2х + 3 = х2 (отриманому за означенням логарифма).
Тобто х2 - 2х - 3 = 0,
х1 = -1, х2 = 3.
В ОДЗ входить тільки х = 3. Отже, . На ОДЗ це рівняння рівносильне рівнянню 2х + 3 = х2 (отриманому за означенням логарифма).
Тобто х2 - 2х - 3 = 0,
х1 = -1, х2 = 3.
В ОДЗ входить тільки х = 3. Отже, 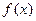 має єдиний нуль функції х = 3.
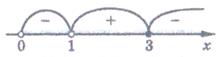
3. Відзначаємо нулі функції на ОДЗ, знаходимо знак має єдиний нуль функції х = 3.
3. Відзначаємо нулі функції на ОДЗ, знаходимо знак 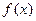 на кожному з проміжків, на які розбивається ОДЗ, і записуємо рішення нерівності на кожному з проміжків, на які розбивається ОДЗ, і записуємо рішення нерівності 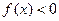 . .
Відповідь: х |
Вправи
Розв'язати нерівність
1)  ;
;
2) 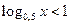 ;
;
3)  ;
;
4) 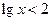 ;
;
5) 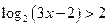 ;
;
6) 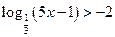 ;
;
7) 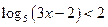 ;
;
8) 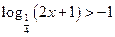 ;
;
9) 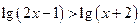 ;
;
10) 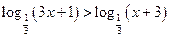 ;
;
11) 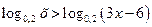 ;
;
12) 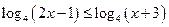 .
.
Дата добавления: 2015-08-26; просмотров: 886;

 (0; 1)
(0; 1)