Методы принятия решений при управлении инновационными проектами
В теории принятия решений (ПР) используются «разумные» процедуры выбора наилучшей из нескольких возможных альтернатив. Доброкачественность выбранного решения зависит от качества данных, используемых при описании ситуации, в которой принимается решение. С этой точки зрения процесс ПР может рассматриваться как:
- ПР в условиях определенности, когда данные известны точно;
- ПР в условиях риска, когда данные можно описать с помощью вероятностных распределений;
- ПР в условиях неопределенности, когда данным нельзя приписать относительные веса, которые представляли бы степень их значимости в процессе ПР.
По существу, в условиях определенности данные надежно определены, в условиях неопределенности они не определены (имеющиеся данные трудно или невозможно классифицировать по степени значимости для ПР, отсутствуют статистические характеристики). ПР в условиях риска, следовательно, представляет «промежуточный» случай.
Модели линейного программирования (ЛП) являются примером ПР в условиях определенности. Эти модели применимы лишь в тех случаях, когда альтернативные решения можно связать между собой точными линейными функциями. Существует однако иной, более общий подход к ПР в ситуациях, когда необходимо определить некоторые количественные показатели, обеспечивающие метрику предпочтений для возможных альтернативных решений. Этот подход, разработанный Т.Саати /23, 24/, известен как метод анализа иерархий (МАИ).
Содержательная и процедурная сложность метода заключается в определении относительных весовых коэффициентов для оценки альтернативных решений. Если имеется n критериев на заданном уровне иерархии, соответствующая процедура создает матрицу А размерности n´n, именуемую матрицей парных сравнений, которая отражает суждение ЛПР относительно важности разных критериев. Парное сравнение выполняется таким образом, что критерий в строке i (i = 1,2,…,n) оценивается относительно каждого из критериев, представленных n столбцами. Обозначим через aij элемент матрицы A, находящийся на пересечении i-строки и j-го столбца. В соответствии с методом для описания упомянутых оценок используются целые числа от 1 до 9. При этом aij =1 означает, что i-й и j-й критерии одинаково важны, aij = 5 отражает мнение, что i-й критерий значительно важнее, чем j-й, а aij = 9 указывает, что i-й критерий чрезвычайно важнее j-го. Другие промежуточные значения между 1 и 9 интерпретируются аналогично. Согласованность таких обозначений обеспечивается следующим условием: если aij = k, то автоматически aji = 1/k. Кроме того, все диагональные элементы aii матрицы A должны быть равны 1, т.к. они выражают оценку критерия относительно самих себя.
Рассмотрим использования МАИ для задачи размещения ресурсов /23/. Ресурс может принять форму материалов, энергии, времени, человеческих усилий, или их комбинаций. Деньги обычно используются для оценки различных величин, характеризующих каждый из этих видов ресурсов.
Чтобы разместить ресурсы, нужно рассмотреть потребности и то, как эти ресурсы следует распределить. Простым случаем будет распределение ресурсов по нескольким альтернативам. Для осуществления этого необходимо определить приоритеты альтернатив согласно их эффективности и стоимости.
Для вычисления эффективности альтернатив необходимо рассмотреть иерархию целей и характеристик альтернатив, а также сами альтернативы, чтобы иметь суждение о том, насколько велик вклад каждой альтернативы в достижение целей. Обычно имеется неопределенность в оценке воздействия альтернатив. Поэтому необходим уровень в иерархии, воспроизводящий неопределенность. За этим уровнем должно следовать представление известных и неизвестных технологических факторов. Таким образом, можно получить оценку приоритетов альтернатив при неопределенности.
Следующим этапом является рассмотрение иерархии для издержек реализации альтернатив. Оценка задачи и того, что требуется для ее решения, часто неопределенны. Иногда необходимо предварительное исследование осуществимости для определения как издержек, так и эффективности решения задачи до построения иерархии.
Имеется три типа задач размещения ресурсов общим количеством Х.
1. Полное вложение капитала. Если начинают новые проекты, которые должны быть завершены за период размещения, то нужно произвести расчет эффективности вi и стоимости сi, перенумеровать проекты так, чтобы идентифицировать их согласно отношению в1/с1 ³ в2/с2 ³ ... ³ вn/сn, и распределить ресурсы в порядке убывания этих соотношений, пока они не исчерпаются.
2. Частичное вложение капитала. В случае, когда требуется начать и следить за выполнением нескольких проектов, а распределение ресурсов производится в течение отдельных периодов времени, решается задача:
n
å(bi/ci)xi = max
i=1
при условиях
n
å xi = X, 0 £ xi £ Ri/X,
i=1
где Ri - требуемое количество ресурса вида деятельности i.
Поэтому не поддерживается проект, в результате реализации которого можно получить меньше, чем сравнительное значение стоимости по отношению к общему наличному ресурсу.
3. Для проектов, которые уже выполняются, можно проводить распределение согласно отношению оставшегося (иногда говорят, маргинального) приоритета к издержкам.
В некоторых случаях может оказаться, что отношение эффективности к стоимости не то, которое хотелось бы иметь, так как некоторые малоэффективные вещи реализуются с очень низкими издержками. Поэтому до проведения анализа “стоимость-эффективность” должны быть определены требования к альтернативам.
Проиллюстрируем использование основных процедур МАИ для определения эффективности и стоимости на примере проектов различных переправы через реку /24/.
Правительственное агентство, обладающее полномочиями на строительство мостов, туннелей и т.д., должно решить, строить или не строить туннель и/или мост через реку, которую в настоящее время обслуживает частный паром.
Факторы, влияющие на эффективность и стоимость переправы через реку, представлены двумя иерархиями на рис.37 и рис. 38. Они относятся к трем категориям: экономической, социальной и окружающей среды. Решение принимается в зависимости от отношения эффективности к стоимости.
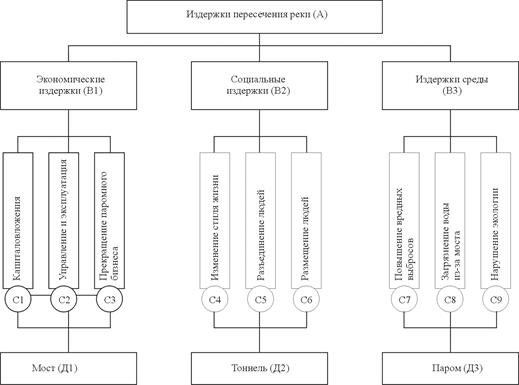
Рис.37.
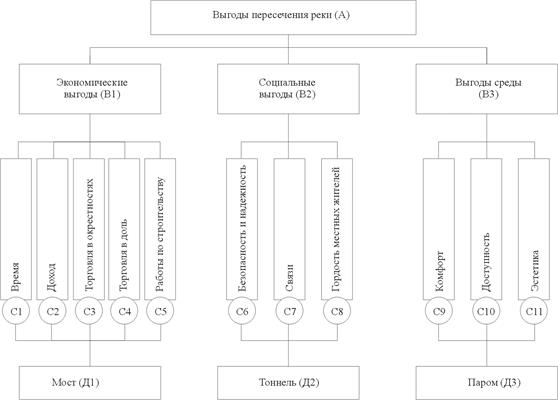
Рис. 38.
Экономические факторы, которые влияют на выбор, определяются выгодой, получаемой в результате экономии времени от пользования мостом или туннелем по сравнению с паромом. Увеличение притока транспорта из-за пределов района может предоставить возможность ввести пошлину, которая добавляется к общему доходу местных властей. Оживление торговли, вызванное увеличением интенсивности транспорта, также выгодно общине в целом. К тому же движение транспорта будет способствовать сопутствующей торговле (например, АЗС, рестораны и т.п.). Имеется также экономическая выгода от строительных работ. Если бы надо было учитывать только эти факторы, то большинство из них можно было бы оценивать количественно. Соответствующие издержки также можно рассчитать, и для ПР мы могли бы использовать отношение эффективности к стоимости. Однако нужно принять во внимание социальные факторы и факторы окружающей среды, которые не переводятся каким-либо разумным способом в доллары.
Социальные выгоды проекта рассматриваются как такие, какие общество в целом получит от наличия моста или туннеля. Они включают обеспечение большей безопасности и надежности, чем паром. Мост или туннель позволяют совершать большее число поездок через реку для посещения родственников, друзей, музеев и т.д. Наконец, они могут стать предметом гордости общины, которая не достигает той же степени при использовании парома.
Факторы окружающей среды рассматриваются с точки зрения их вклада в персональные выгоды. Персональные выгоды отличаются от выгод общества в целом тем, что они менее абстрактны. Факторами окружающей среды, которые представляют интерес для индивидуума, являются удобство пользования мостом, туннелем или паромом, доступность одного по сравнению с другим и эстетика, влияющие на выбор альтернативы переправы через реку.
Так же, как и выгоды, издержки от переправы через реку включают факторы экономические, социальные и окружающей среды. Были приняты во внимание экономические расходы трех видов: капиталовложения на альтернативы, расходы, связанные с эксплуатацией и текущим ремонтом для всех трех проектов, и экономическое следствие закрытия паромного бизнеса.
Социальные издержки представляют собой затраты общества. Важной представляется мысль о том, насколько изменится стиль жизни в зависимости от принятой альтернативы. Перегруженность движения зависит от разумных способов переправы и также считается важной частью издержек. Последней компонентой социальных издержек может быть влияние на общество перемещения людей в соответствии с выбранной альтернативой.
Издержки, порожденные окружающей средой, отличаются от выгод тем, что они представляют возможный вред, причиняемый экосистеме различными альтернативами. Различные способы переправы через реку могут увеличить загазованность в районе. Кроме того, вносят свой вклад в издержки, обусловленные окружающей средой, загрязнение воды и общее разрушение экологии.
При вычислении выгод и издержек экономические факторы первесили другие. Выгоды от торговли вдоль моста, дополнительная безопасность и надежность, а также быстрота переправы через реку - все это получило высокие приоритеты.
Общие выгоды и издержки следующие:
мост туннель паром
выгоды (bi) 0.57 0.36 0.07
издержки (ci) 0.36 0.58 0.05
Критерий, использованный в анализе “стоимость - эффективность” следующий: найти max bi/ci, т.е. выбрать проект с наибольшим отношением выгоды к издержкам.
Для этого примера имеем:
Мост Туннель Паром
b1/c1 = 1.58 b2/c2 = 0.62 b3/c3 = 1.28
Критерий отдает предпочтение строительству моста через реку. Отметим, что здесь приняты во внимание основные требования. Используя маргинальный анализ с издержками 0.05 £ 0.36 £ 0.58 и эффективностями 0.07; 0.57; 0.36, получаем 0.07/0.05; 0.5/0.3 и вновь оказывается, что предпочтительнее всего мост.
Рассмотренную выше задачу можно было бы решить, используя классический подход (анализ «стоимость – эффективность»), который основан на оценке каждого варианта с точки зрения издержек и с точки зрения доходов, которые можно получить при их реализации. Сравнение альтернатив сводится в этом случае к сравнению объемов доходов в расчете на единицу ресурса (т.е. издержек). В этом случае возникают некоторые особенности, не позволяющие эффективно решить рассматриваемую задачу с использованием анализа «стоимость – эффективность». К таким особенностям можно отнести:
- Отношение доходов к издержкам, оцениваемое в стоимостном выражении, по существу не является объективной мерой качества варианта (проекта); не ясно, как, например, оценивать в деньгах выгоды и издержки неосязаемых ценностей (т.е. возникает проблема измерения качественных факторов);
- Известно также, что доходы и издержки распределяются по многим сферам (социальным, политическим, экономическим, управленческим и т.п.) и их взаимосвязь влияет на оценку альтернатив.
Применение МАИ позволяет снять эти проблемы. В этом случае требуется построить две иерархии: одну для издержек, другую для выгод с одними и теми же альтернативами на нижнем уровне. Таким образом, получаются два вектора приоритетов – доходов и издержек. Затем вычисляются отношения доходов к издержкам для каждой альтернативы. Наибольшее значение из этих отношений и определяет лучший проект.
Теперь рассмотрим методы ПР в условиях риска и неопределенности.
Если решение принимается в условиях риска, то стоимости альтернативных решений обычно описываются вероятностными распределениями. По этой причине принимаемое решение основывается на использовании критерия ожидаемого значения, в соответствии с которым альтернативные решения сравниваются с точки зрения максимизации ожидаемой прибыли или минимизации ожидаемых затрат. Предполагается, что прибыль (затраты), связанные с каждым альтернативным решением, является случайной величиной.
При управлении инновационными проектами довольно часто приходится решать задачу выбора проектов для инвестирования, предлагаемых различными компаниями, акции которых представлены на фондовой бирже. В приведенном ниже примере /25/ рассматривается простая ситуация, связанная с ПР при наличии конечного числа альтернатив и точных значений матрицы доходов.
Пример 1
Предположим, что вы хотите вложить на фондовой бирже 10 тыс. долл. в акции одной из двух компаний: А или В. Акции компании А являются рискованными, но могут принести 50% прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиций может обесцениться на 20%. Компания В обеспечивает безопасность инвестиций с 15% прибыли в условиях повышения котировок на бирже и только 5% - в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться, с вероятностью 60% прогнозируют повышение котировок и с вероятностью 40% - понижение котировок. В какую компанию следует вложить деньги?
Информация, связанная с ПР, суммирована в таблице.
| Альтернативное решение | Прибыль от инвестиции за один год | |
| При повышении котировок | При понижении котировок | |
| Акции компании А | -2000 | |
| Акции компании В | ||
| Вероятность события | 0.6 | 0.4 |
Эта задача может быть представлена в виде дерева решений, показанного на рис. 39. На этом рисунке используется два типа вершин: квадратик представляет “решающую” вершину, а кружок - “случайную”. Таким образом, из вершины 1 (“решающая”) выходят две ветви, представляющие альтернативы, связанные с покупкой акций компании А или В. Далее две ветви, выходящие из “случайных” вершин 2 и 3, соответствуют случаям повышения и понижения котировок на бирже с вероятностями их появления и соответствующими платежами.
Исходя из схемы рис. 39, получаем ожидаемую прибыль за год для каждой из двух альтернатив.
Для акций компании А: 5000 долл. ´ 0.6 + (-2000 долл.)´ 0.4 = 2200 долл.
Для акций компании В: 1500 долл. ´ 0.6 + 500 долл. ´ 0.4 = 1100 долл.
Решением, основанным на этих вычислениях, является покупка акций компании А.
Повышение котировок (0.6)

 Инвестиции в 5000 долл.
Инвестиции в 5000 долл.
Дата добавления: 2015-08-26; просмотров: 1089;
