ћетоды исследовани€ операций в управлении инновационными проектами
–ассмотрим особенности применени€ теории исследовани€ операций на примере трех известных методик прогнозировани€ изменений неких переменных как функций времени:
- прогнозирование с использованием скольз€щего среднего;
- прогнозирование путем экспоненциального сглаживани€;
- регрессионное прогнозирование.
»спользуем следующие основные обозначени€:
yt - действительное (или наблюдаемое) значение случайной величины y в момент времени t,
y*t - расчетное значение (оценка) случайной величины y в момент времени t,
et - случайный компонент (или шум) в момент времени t.
ѕрогнозирование с использованием скольз€щего среднего. ѕри использовании этой методики основное предположение состоит в том, что временной р€д €вл€етс€ устойчивым в том смысле, что его члены €вл€ютс€ реализаци€ми следующего случайного процесса:
yt = b + et,
где b - неизвестный посто€нный параметр, который оцениваетс€ на основе представленной информации. ѕредполагаетс€, что случайна€ ошибка et имеет нулевое математическое ожидание и посто€нную дисперсию. роме того, предполагаетс€, что данные дл€ различных периодов времени не коррелированны.
ѕредполагает, что последние n наблюдений €вл€ютс€ равнозначно важными дл€ оценки параметра b. ƒругими словами, если в текущий момент времени t последние n наблюдений есть yt-n+1, yt-n+2 , ... , yt, тогда оцениваемое значение дл€ момента t+1 вычисл€етс€ по формуле:
y*t+1 = (yt-n+1 + yt-n+2 + ... + yt) / n.
Ќе существует четкого правила дл€ выбора числа n - базы метода, использующего скольз€щее среднее. ≈сли есть весомые основани€ полагать, что наблюдени€ в течение достаточно длительного времени удовлетвор€ют модели yt = b + et, то рекомендуетс€ выбирать большие значени€ n. ≈сли же наблюдаемые значени€ удовлетвор€ют приведенной модели в течение коротких периодов времени, то может быть приемлемым и малое значение n. Ќа практике величина n обычно принимаетс€ в пределах от 2 до 10.
ѕример 1.
¬ таблице представлены объемы спроса на некое изделие за прошедшие 24 мес€ца. Ќеобходимо с помощью метода скольз€щего среднего дать прогноз объема спроса на следующий мес€ц (здесь t = 25).
| ћес€ц t | —прос yt | ћес€ц t | —прос yt |
„тобы проверить применимость метода скольз€щего среднего, проанализируем приведенные данные. Ќа рис. 20 нанесены значени€ временного р€да yt. √рафик показывает, что наблюдаетс€ тенденци€ к возрастанию значений yt с течением времени. Ёто, вообще-то, означает, что скольз€щее среднее не будет хорошим предсказателем дл€ будущего спроса. ¬ частности использование большой базы n дл€ скольз€щего среднего неприемлемо в этом случае, т.к. это приведет к подавлению наблюдаемой тенденции в изменении данных. —ледовательно, если мы используем небольшое значение дл€ базы n, то будем находитьс€ в лучшем положении с точки зрени€ отображени€ упом€нутой тенденции в изменении данных.
≈сли мы используем значение n = 3 в качестве базы скольз€щего среднего, то оценка спроса на следующий мес€ц (t = 25) будет равна средней величине спроса за 22, 23 и 24 мес€цы:
y*25 = (62+70+72)/3 = 68 единиц.
ќценка величины спроса в 68 единиц дл€ 25 мес€ца будет использоватьс€ также при прогнозе спроса дл€ t = 26:
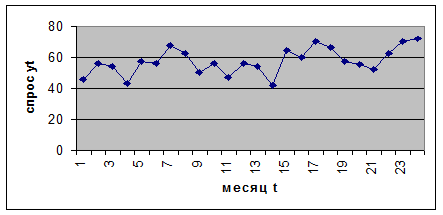
–ис.20
y*26 = (70+72+68)/3 = 70 единиц.
огда значение реального спроса в 25 мес€це будет известно, его следует использовать дл€ вычислени€ новой оценки спроса дл€ 26 мес€ца в виде средней величины спроса 23, 24 и 25 мес€цев.
ћетод экспоненциального сглаживани€ предполагает, что веро€тностный процесс определ€етс€ моделью yt = b + et; это предположение использовалось и при рассмотрении метода скольз€щего среднего. ћетод экспоненциального сглаживани€ разработан дл€ того, чтобы устранить недостаток метода скольз€щего среднего, который состоит в том, что все данные, используемые при вычислении среднего, имеют одинаковый вес. ¬ частности, метод экспоненциального сглаживани€ приписывает больший весовой коэффициент самому последнему наблюдению.
ќпределим величину a (0 < a < 1) как константу сглаживани€, и пусть известны значени€ временного р€да дл€ прошедших t моментов времени y1, y2, ... , yt. “огда оценка y*t+1 дл€ момента времени t+1 вычисл€етс€ по формуле:
y*t+1 = ayt + a(1 - a)yt-1 + a(1 - a)2yt-2 + ... .
оэффициенты при yt, yt-1, yt-2, ... постепенно уменьшаютс€, тем самым эта процедура приписывает больший вес последним (по времени) данным.
‘ормулу дл€ вычислени€ y*t+1 можно привести к следующему (более простому) виду:
y*t+1 = ayt + (1 - a){ayt-1 + a(1 - a)yt-2 + a(1 - a)2yt-3 + ... } = ayt + (1 - a)y*t.
“.о., значение y*t+1 можно вычислить рекуррентно на основании значени€ y*t. ¬ычислени€ в соответствии с этим рекуррентным уравнением начинаютс€ с того, что пропускаетс€ оценка y*t дл€ t = 1 и в качестве оценки дл€ t = 2 принимаетс€ наблюденна€ величина дл€ t = 1, т.е. y*2 = y1. ¬ действительности же дл€ начала можно использовать любую разумную процедуру. Ќапример, часто в качестве оценки y*0 беретс€ усредненное значение yi по УприемлемомуФ числу периодов в начале временного р€да.
¬ыбор константы сглаживани€ a €вл€етс€ решающим моментом при вычислении значени€ прогнозируемой величины. Ѕольшее значение a приписывает больший вес последним наблюдени€м. Ќа практике значение a берут в пределах от 0.01 до 0.30.
ѕример 2.
ѕрименим метод экспоненциального сглаживани€ к данным из прим. 1 при a = 0.1.
¬ таблице содержатс€ результаты вычислений. ѕри вычислени€х пропускаетс€ y*1 и принимаетс€, что y*2 = y1 = 46 единиц.
| i | yi | y*i | i | yi | y*i |
| - | 0.1´56+0.9´51.63 = 52.07 | ||||
| 0.1´54+0.9´52.07 = 52.26 | |||||
| 0.1´56+0.9´46 = 47 | 0.1´42+0.9´52.26 = 51.23 | ||||
| 0.1´54+0.9´47 = 47.7 | 0.1´64+0.9´51.23 = 52.50 | ||||
| 0.1´43+0.9´47.7 = 47.23 | 0.1´60+0.9´52.50 = 53.26 | ||||
| 0.1´57+0.9´47.23 = 48.21 | 0.1´70+0.9´53.26 = 54.93 | ||||
| 0.1´56+0.9´48.21 = 48.98 | 0.1´66+0.9´54.93 = 56.04 | ||||
| 0.1´67+0.9´48.98 = 50.79 | 0.1´57+0.9´56.04 = 56.14 | ||||
| 0.1´62+0.9´50.79 = 51.91 | 0.1´55+0.9´56.14 = 56.02 | ||||
| 0.1´50+0.9´51.91 = 51.72 | 0.1´52+0.9´56.02 = 55.62 | ||||
| 0.1´56+0.9´51.72 = 52.15 | 0.1´62+0.9´55.62 = 56.26 | ||||
| 0.1´47+0.9´52.15 = 51.63 | 0.1´70+0.9´56.62 = 57.63 |
»з приведенных данных следует, что оценка дл€ t = 25 равна
y*25 = ay24 + (1 - a)y*24 = 0.1´72 + 0.9´57.63 = 59.07 единиц.
Ёта оценка значительно отличаетс€ от полученной с помощью метода скольз€щего среднего (68 единиц). Ѕольшее значение дл€ a даст оценку, более близкую к оценке метода скольз€щего среднего.
–егрессионный анализ определ€ет св€зь между зависимой переменной (например, спросом на продукцию) и независимой переменной (например, временем). „асто примен€ема€ формула регрессии, описывающа€ зависимость между переменной y и независимой переменной x, имеет вид:
Y = b0 + b1x + b2x2 + ... + bnxn + e,
где b0, b1, ... , bn - неизвестные параметры. —лучайна€ ошибка e имеет нулевое математическое ожидание и посто€нную дисперсию (т.е. дисперси€ случайной величины e одинакова дл€ всех наблюдаемых значений у).
—ама€ проста€ регрессионна€ модель предполагает, что зависима€ переменна€ линейна относительно независимой переменной, т.е.
y* = a + bx
онстанты a и b определ€ютс€ из временного р€да с использованием метода наименьших квадратов, в соответствии с которым наход€тс€ значени€ этих констант, доставл€ющих минимум сумме квадратов разностей между наблюденными и вычисленными величинами. ѕусть (yi, xi) представл€ет i-ю точку исходных данных временного р€да, i = 1,2,...,n. ќпределим сумму квадратов отклонений между наблюденными и вычисленными величинами.
n
S = å (yi Ц a - bxi)2
i=1
«начени€ коэффициентов a и b определ€ютс€ из соответствующих условий минимума функции S, которые представимы в виде следующих уравнений.
n
ґS/ґa = -2å (yi Ц a - bxi) = 0
i=1
n
ґS/ґb = -2 å (yi Ц a - bxi)xi = 0
i=1
ѕосле алгебраических преобразований получим следующее решение данных уравнений
n __ n _ _ _
b = (å yixi Ц nyx) / (å x2i - nx2) ; a = y - bx,
i=1 i=1
где
_ n _ n
x = å xi / n, y = å yi / n.
i=1 i=1
ѕриведенные соотношени€ показывают, что сначала необходимо вычислить b, а затем величину коэффициента a.
¬ычисленные значени€ a и b имеют силу при любом веро€тностном распределении случайных величин yi. ќднако если yi €вл€етс€ нормально распределенной случайной величиной с посто€нным стандартным отклонением, можно установить доверительный интервал дл€ среднего значени€ оценки при x = x0 (т.е. дл€ y0 = a + bx) в виде интервала
_________________________
__ / _ _
(a + b0) ± ta / 2, n-2 Ö å ni = 1(yi - y*i)2 / (n-2) Ö 1/n + (x0 - x)2 / (åni = 1xi2 - nx2)
¬ыражение (yi - y*i) представл€ет собой отклонение i-го наблюдени€ зависимой переменной от его соответствующей оценки.
ћы заинтересованы в установлении дл€ прогнозируемых значений зависимой переменной y соответствующих им интервалов предсказани€ (скорее чем доверительного интервала дл€ среднего значени€ оценки). ак и следовало ожидать, интервал предсказани€ дл€ значени€ прогнозируемой величины €вл€етс€ более широким, чем доверительный интервал дл€ среднего значени€ оценки. ƒействительно, формула дл€ интервала предсказани€ така€ же как и дл€ доверительного интервала, но с той лишь разницей, что член 1/n под вторым квадратным корнем заменен на (n+1)/n.
„тобы проверить, насколько линейна€ модель y* = a + bx соответствует исходным данным, необходимо вычислить коэффициент коррел€ции r по формуле:
____________________
n __ / n _ n _
r = (åyixi - nyx) / Ö (å xi2 - nx2)(åyi2 - ny2)
i=1 i=1 i=1
где -1 £ r £ 1.
≈сли r = ± 1, тогда линейна€ модель идеально подходит дл€ описани€ зависимости между y и x. ¬ общем случае, чем ближе | r | к 1, тем лучше подходит линейна€ модель. ≈сли же r = 0, величины y и x могут быть независимыми. ¬ действительности равенство r = 0 €вл€етс€ лишь необходимым, но не достаточным условием независимости, т.к. возможен случай, когда дл€ двух зависимых величин коэффициент коррел€ции будет равен 0.
ѕример 3.
ѕрименим модель линейной регрессии к данным из примера 1, которые дл€ удобства приведены в таблице
| ћес€ц, xi | —прос yi | ћес€ц xi | —прос yi |
»з данных этой таблицы получаем следующее
24 24 24 24 24
å yixi = 17842, å xi = 300, å x2i = 4900, å yi = 1374, å y2i = 80254.
i=1 i=1 i=1 i=1 i=1
—ледовательно,
x = 12.5, y = 57.25,
b = (17842 - 24´ 57.25´12.5)/(4900 - 24´(12.5)2),
a = 57.25 - 0.58´12.5 = 50.
“аким образом, оценка спроса представл€етс€ формулой
y* = 50 + 0.58x.
Ќапример, при x = 25 получаем y* = 50+0.58´25 = 64.5 единицы.
¬ычисл€ем коэффициент коррел€ции:
_________________________________
r = (17842 - 24´57.25´12.5) / Ö(4900 - 24´(12.5)2)(80.254 - 24´(57.25)2) = 0.493
ќтносительно малое значение коэффициента коррел€ции r указывает на то, что линейна€ модель y* = 50 + 0.58x €вл€етс€ не совсем подход€щей дл€ исходных данных. —читаетс€, как правило, что линейна€ модель подходит дл€ исходных данных, если 0.75 £ | r | £ 1.
ѕредположим, что необходимо вычислить 95% доверительный интервал дл€ полученной линейной оценки. ƒл€ этого надо сначала вычислить сумму квадратов отклонений от аппроксимирующей пр€мой. ¬ таблице приведены результаты этих вычислений.
| s | d | d* | (d - d*) |
| 50.58 | 20.98 | ||
| 51.16 | 23.43 | ||
| 51.74 | 5.11 | ||
| 54.32 | 86.86 | ||
| 52.90 | 16.81 | ||
| 53.48 | 6.35 | ||
| 54.06 | 152.77 | ||
| 54.64 | 54.17 | ||
| 55.22 | 27.25 | ||
| 55.80 | 0.04 | ||
| 56.38 | 87.98 | ||
| 56.96 | 0.92 | ||
| 57.54 | 12.53 | ||
| 58.12 | 259.85 | ||
| 58.70 | 28.09 | ||
| 59.28 | 0.52 | ||
| 59.86 | 102.82 | ||
| 60.44 | 30.91 | ||
| 61.02 | 16.16 | ||
| 61.60 | 43.56 | ||
| 62.18 | 103.63 | ||
| 62.76 | 0.58 | ||
| 63.34 | 44.53 | ||
| 63.92 | 65.29 | ||
| 24 å (yi - y*i)2 = 1088.70 i=1 |
“абличное значение критери€ —тьюдента t0.025,22 = 2.074. —ледовательно, искомый доверительный интервал имеет вид:
__________ _________________________________
(50 + 0.58x0)±2.074Ö1088.7/(24-2)Ö1/24 + [(x0 - 12.5)2 / (4900 - 24´(12.5)2)].
Ёто выражение можно упростить, в результате получим следующее:
______________________
(50 + 0.58x0)±14.59Ö0.042 + [(x0 - 12.5)2 / 1150.
„тобы продемонстрировать применение этой формулы, вычислим интервал предсказани€ дл€ оценки спроса на следующий мес€ц (x0 = 25). ¬ этом случае коэффициент 0.042 должен быть заменен на (1.042)2, и соответствующий интервал предсказани€ определ€етс€ как (64.5±15.82) или (46.68, 80.32). —ледовательно, можно сказать, что с веро€тностью 95% спрос дл€ x = 25 будет находитьс€ между 46.68 и 80.32 единицами.
¬ыше рассмотрены три метода прогнозировани€ хода инновационного проекта, основанных на теории исследовани€ операций. ѕрименимость каждого из них св€зана с характеристиками временного р€да, представл€ющего исходные данные. ќзнакомитьс€ с другими методиками прогнозировани€ можно, например, по [Е].
—етевое планирование при управлении инноваци€ми
ѕри управлении инновационными проектами имеетс€ р€д ключевых вопросов, на которые необходимо дать ответы. Ёто:
1) —колько времени уйдет на выполнение проекта?
2) ≈сть ли веро€тность отклонени€ от этой оценки?
3) огда отдельные действи€ должны начинатьс€ и заканчиватьс€?
4) акие действи€ €вл€ютс€ критическими при определении времени окончани€ проекта?
5) акова гибкость прочих действий?
Ёти вопросы могут быть проанализированы с помощью сетевых моделей, которые €вл€ютс€ комплексом графических и расчетных методов, организационных меропри€тий и контрольных приемов, обеспечивающих моделирование, анализ и динамическую перестройку выполнени€ сложных проектов, работ и алгоритмов. ќсновным элементом модели €вл€етс€ сетевой график.
ѕреимущества такого подхода заключаютс€ в следующем:
- сетевые графики €вл€ютс€ относительно простыми инструментами, позвол€ющими управл€ть сложными проектами;
- сетевые графики позвол€ют принимать решени€ при перепланировании ресурсов, когда это необходимо;
- сетевые графики позвол€ют руководителю свер€ть ход выполнени€ проекта с контрольными сроками.
ќднако на практике часто трудно оценить продолжительность действий в рамках проекта; или затруднительно определение взаимозависимости некоторых действий в рамках сложного проекта; или анализ нескольких видов необходимых ресурсов повышает сложность задачи.
—етевое моделирование Ц это один из методов системного подхода к управлению сложными динамическими системами с целью обеспечени€ определенных оптимальных показателей. ¬ основе сетевого моделировани€ лежит изображение планируемого комплекса работ в виде графа. ƒадим некоторые основные определени€.
√раф Ц это схема, состо€ща€ из заданных точек (вершин), соединенных определенной системой линий. ќтрезки, соедин€ющие вершины, называютс€ ребрами (дугами) графа.
“еори€ графов оперирует пон€тием пути, под которым понимаетс€ така€ последовательность ребер, когда конец каждого предыдущего ребра совпадает с началом последующего, т.е. конечна€ вершина каждой предыдущей дуги совпадает с начальной вершиной следующей дуги.
—етевой график - это ориентированный граф без контуров, ребра которого имеют одну или несколько числовых характеристик. ¬ сетевом графике различают два основных элемента: работу и событие.
–аботами называютс€ любые процессы, действи€, привод€щие к достижению определенных результатов (событий). –абота представл€ет собой процесс, происход€щий во времени.
—обыти€ми называютс€ результаты произведенных работ. —обытие конкретизирует процесс планировани€, исключает возможность различного толковани€ итогов выполненных работ.
¬ сетевом графике событие изображаетс€ кружком, пр€моугольником или другой геометрической фигурой, а работа Ц в виде пр€мой или дуги. »ногда на одном графике событи€ обозначаютс€ различными фигурами, чтобы выделить определенные этапы, например, технологического процесса.
—обытие, которое не имеет предшествующих событий, называетс€ исходным (начальным). —обытие, которое не имеет последующих событий и отражает конечную цель комплекса работ, включенных в данную сеть, называетс€ завершающим (конечным).
Ћюба€ последовательность событий в сетевом графике называетс€ путем. ѕуть между исходным и завершающим событи€ми в сетевом графике, имеющий наибольшую продолжительность, называетс€ критическим.
—етевые модели могут быть ориентированы на событи€ или на работы. ¬ сет€х, ориентированных на событи€, вершинами графа €вл€ютс€ результаты выполнени€ работ, т.е. операций, процессов или каких-либо иных действий. ¬ сет€х, ориентированных только на работы, вершинами €вл€ютс€ работы, которые изображаютс€ кружками или другими геометрическими фигурами, а пунктирными стрелками Ц св€зи между ними. “акими св€з€ми могут быть, например, технологические, ресурсные, организационные и др. св€зи.
¬ сетевых графиках, вершины которых обозначают событи€, работы обозначаютс€ дугой между двум€ событи€ми. ≈сли дуга соедин€ет два событи€ i и i+1, то работа обозначаетс€ как (i, i+1).
—етевые оптимизационные модели обычно €вл€ютс€ частными случа€ми моделей линейного программировани€. „аще всего они используютс€ в задачах распределени€ ресурсов и составлени€ расписаний. ’от€ большинство сетевых задач можно решать методами линейного программировани€, дл€ их эффективного решени€ разработаны специальные методы, учитывающие структуру сетевых моделей.
Ќаиболее известные - метод критического пути (critical path method, сокращенно CPM), а также система планировани€ и руководства программами разработок (program evaluation and review technique, сокращенно PERT). ¬ этих методах проекты рассматриваютс€ как совокупность некоторых взаимосв€занных процессов (видов де€тельности, этапов или фаз выполнени€ проекта), каждый из которых требует определенных временных и других ресурсов. ¬ методах CPM и PERT проводитс€ анализ проектов дл€ составлени€ временных графиков распределени€ фаз проектов.
ќсновные этапы выполнени€ этих методов обобщенно можно представить следующим образом. Ќа первом этапе определ€ютс€ отдельные процессы, составл€ющие проект, их отношени€ предшествовани€ (т.е. какой процесс должен предшествовать другому) и их длительность. ƒалее проект представл€етс€ в виде сети, показывающей отношени€ предшествовани€ среди процессов, составл€ющих проект. Ќа третьем этапе на основе построенной сети выполн€ютс€ вычислени€, в результате которых составл€етс€ временной график реализации проекта.
ћетоды CPM и PERT, которые разрабатывались независимо друг от друга, отличаютс€ тем, что в методе критического пути длительность каждого этапа проекта €вл€етс€ детерминированной, тогда как в системе планировани€ PERT - стохастической. ¬ насто€щее врем€ создано большое число модификаций сетевых методов.
—етевое планирование начинаетс€ с составлени€ перечн€ работ и оценок их продолжительности. аждый процесс проекта обозначаетс€ в сети дугой, ориентированной по направлению выполнени€ проекта. ”злы сети (также называемые событи€ми) устанавливают отношени€ предшествовани€ среди процессов проекта.
ѕри этом работы изображаютс€ стрелками, направление которых указывает продвижение работ по проекту (рис.21). —обыти€, соответствующие началу и завершению работ (или моменты времени), изображаютс€ в виде узлов сети, которые нумеруютс€ соответствующим образом.

–ис.21. —етевой график проекта
ѕостроение сети проекта построено на следующих правилах.
ѕравило 1. аждый процесс в проекте представим одной и только одной дугой.
ѕравило 2. аждый процесс идентифицируетс€ двум€ концевыми узлами.
Ёто означает, что участок сети вида
–абота 1
 |  |
–абота 2
неверно отображает две одновременно завершающиес€ работы. ¬ такой ситуации участок сети должен иметь вид

–абота 1
‘иктивна€ работа
–абота 2
‘иктивна€ работа не требует ни времени, ни ресурсов; она вводитс€ только дл€ целей однозначности событий, св€занных с завершением работ. “акой прием используетс€ в ситуаци€х, когда работы 3 и 4 должны следовать за работой 2, но работа 1 не об€зательно должна предшествовать работе 4, т.е.
 –абота 1 –абота 3
–абота 1 –абота 3
–абота 2 –абота 4
ѕравило 3. ƒл€ поддержани€ правильных отношений предшествовани€ при включении в сеть любого процесса необходимо ответить на следующие вопросы:
а) какой процесс непосредственно предшествует текущему;
б) какой процесс должен выполн€тьс€ после завершени€ текущего процесса;
в) какой процесс конкурирует (выполн€етс€ параллельно) с текущим.
—оотношение предшествовани€ Ц следовани€ должны соблюдатьс€ на всем прот€жении сети. ѕредположим, например, что работа 6 следует за работами 4 и 2, которые, в свою очередь следуют за работой 3. “огда участок сети
 –абота 4
–абота 4
 –абота 3
–абота 3
 |  |  |
 –абота 2 –абота 6
–абота 2 –абота 6
 | |||
 | |||
€вл€етс€ правильным только в том случае, если работа 4 будет завершена прежде, чем может начатьс€ работа 6.
Ёти три правила иллюстрируютс€ с помощью сети, представленной на рис. 21.
–ассмотрим пример, иллюстрирующий построение сети проекта издани€ книги.
»здатель имеет контракт с автором на издание его книги. Ќиже представлена последовательность (упрощенна€) процессов, привод€щих к реализации проекта издани€ книги. Ќеобходимо разработать сеть дл€ этого проекта.
| ѕроцесс | ѕредшествующий процесс | ƒлительность (недели) |
| ј: ѕрочтение рукописи редактором ¬: ѕробна€ верстка отдельных страниц книги —: –азработка обложки книги D: ѕодготовка иллюстраций ≈: ѕросмотр автором редакторских правок и сверстанных страниц F: ¬ерстка книги (создание макета книги) G: ѕроверка автором макета книги H: ѕроверка автором иллюстраций I: ѕодготовка печатных форм J: ѕечать и брошюровка книги | - - - - ј, ¬ ≈ F D G, H C, I |
Ќа рис. 22 показана сеть, представл€юща€ взаимосв€зь процессов данного проекта. ‘иктивный процесс (2, 3) введен дл€ того, чтобы УразвестиФ конкурирующие процессы ј и ¬. Ќомера узлов сети возрастают в направлении выполнени€ проектов.
≈-2 F-2 G-2
 |  |  |
 H-1
H-1
 ј-3 D-3 I-2
ј-3 D-3 I-2
 C-4 J-4
C-4 J-4
 | 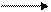 |
–ис. 2. —еть проекта издани€ книги
јнализ методом критического пути заключаетс€ в использовании сетевых графиков при определении УкритическихФ меропри€тий проекта. ритические действи€ не гибкие и должны начинатьс€ и заканчиватьс€ воврем€ дл€ того, чтобы проект был завершен в срок.
онечным результатом применени€ метода критического пути будет построение временного графика выполнени€ проекта. ƒл€ этого провод€тс€ специальные вычислени€, в результате чего получаем следующую информацию:
а) обща€ длительность выполнени€ проекта;
б) разделение множества процессов, составл€ющих проект, на критические и некритические.
ѕроцесс €вл€етс€ критическим, если он не имеет УзазораФ дл€ времени своего начала и завершени€. “.о., чтобы весь проект завершилс€ без задержек, необходимо, чтобы все критические процессы начинались и заканчивались в строго определенное врем€. ƒл€ некритического процесса возможен некоторый УдрейфФ времени его начала, но в определенных границах, когда врем€ его начала не вли€ет на длительность выполнени€ всего проекта.
ƒл€ проведени€ необходимых вычислений определим событие как точку на временной оси, где завершаетс€ один процесс и начинаетс€ другой. ¬ терминах сети, событие - это сетевой узел. ¬ведем также следующие обозначени€ и определени€.
Ÿ j - самое раннее возможное врем€ наступлени€ событи€ j;
Dj - самое позднее возможное врем€ наступлени€ событи€ j;
Dij - длительность процесса (i, j).
¬ычисление критического пути включает два этапа (прохода). ѕри проходе вперед вычисл€ютс€ самые ранние времена наступлени€ событий, а при проходе назад - самые поздние времена наступлени€ тех же событий.
ѕроход вперед. «десь вычислени€ начинаютс€ в узле 1 и заканчиваютс€ в последнем узле n.
Ќачальный шаг. ѕолагаем Ш 1 = 0; это указывает на то, что проект начинаетс€ в нулевой момент времени.
ќсновной шаг j. ƒл€ узла j определ€ем узлы p, q, ..., v, непосредственно св€занные с узлом j процессами (p, j), (q, j),..., (v, j), дл€ которых уже вычислены самые ранние времена наступлени€ соответствующих событий. —амое раннее врем€ наступлени€ событи€ j вычисл€етс€ по формуле
Ш j = max { Ш p + Dpj, Ш q + Dqj,..., Ш v + Dvj}.
ѕроход вперед завершаетс€, когда будет вычислена величина ž n дл€ узла n. ѕо определению величина ž j равна самому длинному пути (длительности) от начала проекта до узла (событи€) j.
ѕроход назад. ¬ этом проходе вычислени€ начинаютс€ в последнем узле n и заканчиваютс€ в узле 1.
Ќачальный шаг. ѕолагаем Dn º Ш n; это указывает, что самое раннее и самое позднее времена дл€ завершени€ проекта совпадают.
ќсновной шаг j. ƒл€ узла j определ€ем узлы p, q, ..., v, непосредственно св€занные с узлом j процессами (p, j), (q, j),..., (v, j), дл€ которых уже вычислены самые поздние времена наступлени€ соответствующих событий. —амое позднее врем€ наступлени€ событи€ j вычисл€етс€ по формуле
Dj = min {Dp - Dpj, Dq - Dqj,..., Dv - Dvj}.
ѕроход назад завершаетс€ при вычислении величины D1 дл€ узла 1.
ѕроцесс (i, j) будет критическим, если выполн€ютс€ три услови€:
1. Di = ž i
2. Dj = ž j
3. Dj - Di = ž j - ž i = Dij
≈сли эти услови€ не выполн€ютс€, то процесс некритический.
ритические процессы должны образовывать непрерывный путь через всю сеть от начального событи€ до конечного.
ѕример 1.
Ќайдем критический путь дл€ сети проекта, показанной на рис. 23. ƒлительность всех процессов дана в дн€х.
ќбозначени€:

 ѕроход вперед: ‘ ‘
ѕроход вперед: ‘ ‘
 ѕроход назад: D D
ѕроход назад: D D
F ритический путь: O Ѓ O
B 2 E 11
C G
A
H
5 1
D
–ис.23
ѕроход вперед.
”зел 1. ѕолагаем ‘ 1 = 0.
”зел 2. ‘ 2 = ‘ 1 + D12 = 0 + 5 = 5.
”зел 3. ‘ 3 = max {‘ 1 + D13, ‘ 2 + D23} = max {0 + 6, 5 + 3}= 8.
”зел 4. ‘ 4 = ‘ 2 + D24 = 5 + 8 =13.
”зел 5. ‘ 5 = max {‘ 3 + D35, ‘ 4 + D45} = max {8 + 2, 13 + 0} = 13.
”зел 6. ‘ 6 = max {‘ 3 + D36, ‘ 4 + D46, ‘ 5 + D56} = max {8 + 11, 13 + 1, 13 + 12} = 25.
“аким образом, расчеты показывают, что проект можно выполнить за 25 дней.
ѕроход назад.
”зел 6. ѕолагаем D6 = Ш 6 = 25.
”зел 5. D5 = D6 - D56 = 25 - 12 = 13.
”зел 4. D4 = min {D6 - D46, D5 - D45} = min{25 - 1, 13 - 0} = 13.
”зел 3. D3 = min{D6 - D36, D5 - D35} = min{25 - 11, 13 - 2} = 11.
”зел 2. D2 = min{D4 - D24, D3 - D23} = min{13 - 8, 11 - 3} = 5.
”зел 1. D1 = min{D3 - D13, D2 - D12} = min{11 - 6, 5 - 5} = 0.
¬ычислени€ без ошибок всегда привод€т к результату D1 = 0.
–езультаты вычислений, выполн€емых при проходах вперед и назад, показаны на рис. 3. ѕравила определени€ критических процессов показывают, что критический путь составл€ют процессы 1Ѓ2Ѓ4Ѓ5Ѓ6, т.е. этот путь проходит от начального узла 1 до конечного узла 6. —умма длительностей критических процессов (1, 2), (2, 4), (4, 5) и (5, 6) равна длительности всего проекта (т.е. 25 дней). ќтметим, что процесс (4, 6) удовлетвор€ет первым двум услови€м критического пути (D4 = Ш 4 = 13 и D6 = Ш 6 = 25), но не удовлетвор€ет третьему условию ( € 6 - Ш 4 ¹ D46). ѕоэтому данный процесс не €вл€етс€ критическим.
ќбща€ продолжительность проекта €вл€етс€ важным фактором при управлении проектами, требующими проведени€ большого количества меропри€тий. ќбщую продолжительность можно рассчитать по сетевому графику при условии, что известна продолжительность каждого меропри€ти€, требуемого в соответствии с проектом (график √антта).
Ќа графике √антта отмечаетс€ врем€ начала и окончани€ действи€ и с его помощью легко увидеть, какие из действий должны проистекать в любой временной точке. √рафик √антта особенно полезен при управлении проектом и планировании ресурсов. Ќапомним, что i дл€ процесса (i, j) указывает на самое раннее врем€ начала этого процесса, Dj - на самое позднее врем€ завершени€ процесса. “аким образом, пара величин (Ш i, Dj) ограничивает максимальный интервал времени, в течение которого может выполн€тьс€ процесс (i, j).
ѕример 2.
ѕостроим временной график проекта из примера 1 (рис. 23).
ѕредварительный временной график проекта можно начертить, использу€ максимальные интервалы выполнени€ каждого процесса. ¬ результате получим график, представленный на рис. 24. —делаем два замечани€.
1. ритические процессы (показаны на графике сплошными лини€ми) располагаютс€ последовательно друг за другом без временных зазоров и перекрытий. “аким образом, их суммарна€ длительность равна длительности выполнени€ всего проекта (здесь 25 дней).
2. Ќекритические процессы (показаны на графике пунктирными лини€ми) представлены максимальными интервалами выполнени€, которые превышают реальную длительность выполнени€ этих процессов. ѕоэтому необходимо каким-то образом определитьс€ с началом выполнени€ этих процессов.
ак выбрать врем€ начала выполнени€ некритического процесса? ќбычно предпочитают начинать некритические процессы (по возможности) в самый ранний срок. ¬ этом случае остаетс€ запас времени (остаток максимального интервала выполнени€), который можно использовать дл€ решени€ неожиданно возникших во врем€ выполнени€ процесса проблем. ¬месте с тем при необходимости можно перенести начало выполнени€ какого-либо процесса. ƒопустим, если в нашем примере во врем€ выполнени€ процессов E и F (рис.24) используетс€ одно и то же оборудование, причем в каждый момент времени его можно задействовать только дл€ одного процесса, тогда можно исключить временное наложение этих процессов, начав процесс F после завершени€ E.

ј - 5
ритические
D - 8 процессы
G - 12
B - 6
Ќекритические
C - 3
E - 2 процессы
F - 11
H - 1
 |  |
5 10 15 20 25
ƒни
–ис.24
≈сли на некритические процессы не накладываютс€ какие-либо дополнительные ограничени€, и все они начинаютс€ в самый ранний момент времени, то временной график проекта строитс€ автоматически. ќднако в этом случае могут нарушатьс€ некоторые отношени€ предшествовани€. ¬ частности, в примере (см. рис.3) процесс — должен быть завершен до начала процесса ≈. Ќо максимальные интервалы времени выполнени€ этих процессов перекрываютс€, поэтому и реальные интервалы времени их выполнени€ также могут перекрыватьс€. ѕоэтому необходимо предусмотреть какие-нибудь Украсные флажкиФ, которые автоматически указывали бы, когда тот или иной процесс может начинатьс€ без нарушени€ отношений предшествовани€ с другими процессами.
ќпределение запасов времени. «апас времени некритического процесса - это часть максимального интервала времени выполнени€ этого процесса (который больше реальной длительности процесса). –азличают общий запас времени и свободный запас времени процесса.
Ќа рис. 25 показана разность между этими запасами времени процесса (i, j) - общим (TFij) и свободным (FFij). ќбщий запас времени процесса (i, j) определ€етс€ как превышение над длительностью выполнени€ этого процесса интервала времени от самого раннего момента осуществлени€ событи€ i до самого позднего времени осуществлени€ событи€ j, т.е.
TFij = Dj - Ш i - Dij.
—вободный запас времени процесса (i, j) определ€етс€ как превышение над длительностью выполнени€ этого процесса интервала времени от самого раннего момента осуществлени€ событи€ i до самого раннего времени осуществлени€ событи€ j, т.е.
FFij = Ш j - Ш i - Dij.
ѕо определению FFij £ TFij.
ѕравило Украсного флажкаФ. ƒл€ некритического процесса (i, j)
а) если FFij = TFij, тогда данный процесс может выполн€тьс€ в любое врем€ внутри максимального интервала ( Ш i, Dj) без нарушени€ отношений следовани€;
б) если FFij < TFij, тогда без нарушени€ отношений следовани€ данный процесс может начатьс€ со сдвигом, не превышающим FFij, относительно самого раннего момента начала процесса Ш i. —двиг начала процесса на величину времени, превышающую FFij (но не более TFij), должен сопровождатьс€ равным сдвигом относительно всех процессов, начинающихс€ с событи€ j.

j
TFij = Dj - ™ i - Dij
FFij = € j - € i - Dij
i j
Dij
i j
–ис.25
Ёто правило означает, что некритический процесс (i, j) помечаетс€ Украсным флажкомФ только тогда, когда FFij < TFij. Ётот флажок принимаетс€ во внимание при сдвиге начала процесса относительно самого раннего времени на такую величину, при которой следует рассчитывать сдвиг процессов, следующих из узла j.
ѕример 3.
¬ычислим запасы времени дл€ некритических процессов в сети проекта из примера 1 и на основе этих расчетов построим окончательный временной график проекта.
ќбщие и свободные запасы времени некритических процессов представлены в таблице. “акие расчеты можно проводить непосредственно на сети проекта, как показано на рис.25.
| Ќекритический процесс | ƒлительность процесса | ќбщий запас времени (TF) | —вободный запас времени (FF) |
| ¬(1, 3) | 11 Ц 0 Ц 6 = 5 | 8 Ц 0 Ц 6 = 2 | |
| —(2, 3) | 11 Ц 5 Ц 3 = 3 | 8 Ц 5 Ц 3 = 0 | |
| ≈(3, 5) | 13 Ц 8 Ц 2 = 3 | 13 Ц 8 Ц 2 = 3 | |
| F(3, 6) | 25 Ц 8 Ц 11 = 6 | 25 Ц 8 Ц 11 = 6 | |
| H(4, 6) | 25 Ц 13 Ц 1 = 11 | 25 Ц 13 Ц 1 = 11 |
ѕравило Украсного флажкаФ следует примен€ть только к процессам B и C, поскольку дл€ них FF < TF. ќставшиес€ процессы (E, F, H) имеют FF = TF, поэтому они могут выполн€тьс€ в любое врем€ внутри своих максимальных интервалов времени выполнени€.
–ассмотрим процесс ¬, помеченный Украсным флажкомФ. ѕоскольку дл€ этого процесса TF = 5 дней, он может начатьс€ в любой день из интервала 0 - 5 дней от начала выполнени€ всего проекта (рис.3). Ќо если FF = 2 дн€, то, поскольку процесс ¬ начнетс€ в 0-й, 1-й или 2-й день от начала выполнени€ проекта, это не окажет никакого эффекта на последующие процессы E и F. ќднако, если процесс ¬ начнетс€ в (2 + D)-й день (2 + D < 5), начало выполнени€ процессов ≈ и F необходимо сдвинуть от самого раннего срока их начала (8-й день от начала выполнени€ проекта) на величину, не меньшую D; только при таком условии не нарушатс€ отношени€ следовани€ между процессами B, E, F.
ƒл€ помеченного Украсным флажкомФ процесса — имеем FF = 0. Ёто означает, что любой сдвиг начала выполнени€ этого процесса должен сопровождатьс€ таким же (не меньшим) сдвигом начала выполнени€ процессов E и F.
¬ случае »ѕ задачами распределени€ ресурсов, по существу, €вл€ютс€ задачи определени€ сроков исполнени€ проекта, при которых возможно либо выравнивание потребности в ресурсах при соблюдении ограничений на длительность выполнени€ проекта, либо минимизаци€ длительности выполнени€ проекта при ограничени€х на трудовые ресурсы, либо минимизаци€ общей стоимости ресурсов и штрафов за задержку выполнени€ проекта. –ешение последней из перечисленных задач с помощью моделировани€ приводитс€ в работе /20/. Ќаибольшее внимание, однако, удел€лось первым двум задачам. ¬виду их комбинаторного характера возможность получени€ оптимальных решений средствами математического программировани€ очень ограничена. —аудер убедилс€ в неэффективности использовани€ алгоритмов целочисленного и булевого программировани€, т.к. они не сход€тс€ при разумной длительности счета. Ѕыли предложены алгоритмы, основанные на методе ветвей и границ, применимые, однако, только дл€ сетей с числом узлов меньше 50 /11/.
¬виду отсутстви€ успеха в области создани€ методов оптимизации основное внимание удел€лось развитию эвристических методов, позвол€ющих получить приемлемое решение при некоторых разумных правилах установлени€ приоритета работ, выполн€емых с использованием ресурсов, на которые существуют ограничени€. Ёти методы дел€тс€ на УпоследовательныеФ и УпараллельныеФ в зависимости от того, устанавливаетс€ ли приоритет до начала составлени€ графика выполнени€ проекта или постепенно в процессе составлени€ графика. ’от€ большинство опубликованных исследований посв€щено параллельным методам, относительна€ ценность каждого из них все еще не установлена. ƒэйвис /11/ дал подробный обзор работ в этой области и оценку большого числа эвристических методов установлени€ приоритета работ в процессе календарного планировани€. ≈го основной вывод заключаетс€ в том, что, хот€ ни один из эвристических подходов не может всегда давать наилучший график, правило упор€дочени€, в соответствии с которым первой выполн€етс€ работа с наименьшим резервом (или эквивалентное правило минимизации самого позднего времени начала), в среднем дает наилучшие результаты.
„асто возникает необходимость оценить веро€тность того, будет ли отдельна€ работа, некотора€ совокупность работ или проект в целом закончены к определенному сроку. ѕодобна€ формулировка задачи, котора€ была основой при первоначальной разработке метода PERT, предполагает использование трех видов оценок длительности каждой работы в сети: to - оптимистической оценки длительности, tm - модальной оценки, т.е. оценки наиболее веро€тной длительности, tp - пессимистической оценки длительности. ѕредполагаетс€, что гипотетическое распределение фактической длительности выполнени€ работы описываетс€ b-распределением. ћатематическое ожидание te и дисперси€ si дл€ b-распределени€, определ€ющиес€ выражени€ми te = (to + 4tm + tp)/6, si = [(tp - to)/6}2, могут быть вычислены дл€ каждой работы сети. ¬ этом случае ожидаемое врем€ завершени€ Te всего проекта находитс€ как сумма величин te (которые аналогичны длительност€м работ при использовании метода критического пути) дл€ работ, составл€ющих путь наибольшей длины через сеть. ƒалее дл€ любого подмножества критических работ S могут быть вычислены доверительные границы длительности по следующей формуле (котора€ основана на центральной предельной теореме дл€ суммы независимых случайных величин):
______
Tc,s = å(te)j ± KÖ å(si)j,
jÎS jÎS
где K - константа, завис€ща€ от степени достоверности (K=3 дл€ степени достоверности 99.7%, K=2 дл€ степени достоверности 95% и т.д.). ќбычно УоптимальнымФ считаетс€ такой план выполнени€ проекта, дл€ которого Tc,s £ DCs, где DC - желательный срок завершени€ множества работ S. ƒл€ сетевых графиков, которые не удовлетвор€ют этому критерию, можно прибегнуть к перераспределению ресурсов с ненапр€женных работ на критический путь, к увеличению затрат или более радикальным способам перепланировки проекта, пока не будет удовлетворено требование по этому критерию.
—ледует заметить, что все сказанное выше основываетс€ на предположении, что цель заключаетс€ в оценке времени завершени€ проекта. ¬ большинстве случаев это соответствует действительности. ќднако, если руководитель проекта считает, что заданный срок окончани€ легко достижим, например Tc,s значительно меньше Dcs, тогда кроме обычного резервного времени (определ€емого критическим путем) возникает дополнительное УсвободноеФ резервное врем€, обусловленное тем, что Tc,s меньше Dcs.
ћногие проекты научных исследований и разработок часто подвержены действию случайных факторов, т.е. состав работ, выполн€емых после завершени€ некоторого этапа, может измен€тьс€ в зависимости от некоторых условий. Ќапример, химик, занимающийс€ синтезом и испытанием нового инсектицида, должен сознавать, что возможно несколько результатов: неудача, испытани€ прошли нормально, получен уникальный результат. аждый из этих результатов может привести к необходимости выполнени€ р€да последующих работ. ѕоэтому, если используетс€ метод PERT или критического пути, результирующа€ сеть, изображающа€ все св€зи между работами над первичным проектом, будет большой и громоздкой. ѕри этом существует веро€тность того, что с помощью одной схемы не удастс€ полностью отобразить проект. «адачи этого типа можно изобразить с помощью сетей типа дерева с точками прин€ти€ решений (рис.26).
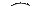
–=0.6 –абота 3
 |  |
–абота 1 –абота 2

 –=0.3 –абота 4 –абота 6
–=0.3 –абота 4 –абота 6
 |  |  |  |
–=0.1 –абота 5 – Ц веро€тность исхода

- точка прин€ти€ решени€
–ис.26. —еть с возможными пут€ми
«аметим, что резервы времени 4-6 и 5-6 €вл€ютс€ условными: если в узле 3 получен результат такой, что выбираетс€ работа 3 или работа 5, то весь проект сокращаетс€ на соответствующую одному из имеющихс€ резервов величину. ¬се прочие расчеты сети производ€тс€ так же, как описано ранее, за исключением того, что результаты этих вычислений должны учитывать веро€тность соответствующего результата. Ќапример, на рис.6 ожидаемое врем€ завершени€ в узле 7 следует вычисл€ть по формуле: te6 + (0.6te3 + 0.3te4 + 0.1te5) + te2 + te1, где tej - математическое ожидание длительности j-й работы.
–ассмотренные выше сетевые методы могут быть применены к планированию нескольких проектов, руководство которыми осуществл€етс€ одной организацией. –ассмотрим, например, портфель из четырех проектов научных исследований (рис.27).

–ис. 27.—етевой график дл€ комплексной программы
ак видно из рисунка, проект ј должен быть завершен до того, как сможет начатьс€ проект ¬ (например, проект ј должен произвести сырье дл€ проекта ¬). ѕроект X и проект Y могут начатьс€ и закончитьс€ в любое врем€ в интервале между моментами а и е. “аким образом, пунктирные линии на рис.27 отображают лишь фиктивные зависимости и служат дл€ того, чтобы указать общий диапазон времени дл€ всех четырех проектов. Ќа этих фиктивных св€з€х, если они имеютс€, можно проставить длительности выполнени€ проектов и таким путем получить ранний срок начала и поздний срок окончани€ проекта. –езервное врем€ дл€ отдельных проектов, образующеес€ за счет этих фиктивных работ, можно использовать так же, как фиктивные работы в сет€х дл€ автономного проекта.
ѕредположим, например, что проекты ¬ и X используют одни и те же ресурсы и что потребность в этих ресурсах превышает их наличие в случае необходимости одновременной реализации проектов ¬ и X. »з рис.27 видно, что начало проекта X можно задержать до момента d, сосредоточив все ресурсы полностью на проекте ¬. ѕосле того как проект ¬ будет завершен, эти ресурсы можно будет использовать дл€ выполнени€ проекта X.
ƒруга€ возможность состоит в том, чтобы оба проекта использовали эти ресурсы с пониженной интенсивностью и при этом оба проекта будут задерживатьс€ (на столько, чтобы не выйти за пределы момента е). ѕроцедуры ускорени€ выполнени€ работ за счет повышени€ затрат, описанные выше, могут быть применимы и к отдельным проектам. “.о., методы сетевого планировани€ дл€ комплексных проектов полностью аналогичны сетевым методам, примен€емым дл€ отдельных проектов.
—уществует, однако, еще один важный аспект планировани€ комплексных работ - приоритет отдельных проектов. ѕредположим, что проект X (рис.27) считаетс€ наиболее УважнымФ из всех проектов. ћогут, например, существовать веские основани€ дл€ того, чтобы руководитель считал необходимым сначала начать данный проект, а не любой другой. ќдной из таких причин могла бы быть опасность конкуренции. ѕриоритетность отдельных проектов может использоватьс€ в качестве весового множител€ при календарном планировании и распределении ресурсов между конкурирующими проектами в системах комплексных проектов.
¬ообще говор€, последовательные изменени€ в сетевых графиках проектов позвол€т руководител€м на уровне проекта и на уровне отдела создавать интегрированные планы. –уководитель каждого проекта может представить на рассмотрение оптимальный сетевой график. Ёти графики могут быть затем объединены в одну сеть комплексного проекта, на основе чего разработано несколько графиков дл€ комплексного проекта при различных предположени€х относительно приоритетов, ресурсов и т.п. Ёти варианты графиков выполнени€ комплексного проекта могут быть затем обсуждены на совещани€х сотрудников, проводимых каждым руководителем отдельного проекта и руководителем комплексного проекта, например заместителем директора фирмы по научно-исследовательской работе. ѕосле этого, исход€ из результатов обсуждени€ всех составных частей и высказанных при этом замечаний, может быть выбран наилучший сетевой график комплексного проекта. ѕрежде чем будет разработан приемлемый общий план работ, может потребоватьс€ несколько последовательных итераций разработки графика работ между уровнем управлени€ отдельным проектом и уровнем комплексного проекта.
¬ыше были рассмотрены различные приемы, призванные помочь в управлении »ѕ. Ёти приемы свод€тс€ в основном к проведению анализа с помощью сетевых графиков. ¬ процессе этого выполн€ютс€ следующие действи€:
- составл€етс€ сетевой график, отображающий весь проект и его составные части;
- проводитс€ анализ методом критического пути. ѕри этом определ€етс€ оценочна€ продолжительность отдельных действий и анализируетс€ степень подвижности каждого из действий. ƒействи€, не имеющие подвижности, считаютс€ критическими. ѕродолжительность таких действий нельз€ изменить без ущерба дл€ продолжительности всего проекта. ƒругие действи€, которые не оказывают немедленного воздействи€ на продолжительность проекта, считаютс€ не критическими. “акого рода анализ отдельных действий проводитс€ с помощью сетевых графиков;
- проводитс€ распределение ресурсов. —оставление графиков (диаграмм) √антта на основе сетевых графиков позвол€ет руководителю проанализировать ресурсы, необходимые дл€ выполнени€ проекта. ѕри недостатке ресурсов можно с помощью графиков √антта перепланировать действи€;
- анализируетс€ возможность сокращени€ сроков. ¬ процессе перепланировани€ проекта, возможно, потребуетс€ сократить сроки отдельных действий, в результате этого могут изменитьс€ ресурсные и стоимостные показатели проекта. —ледовательно, руководитель может проанализировать, какие действи€ сократить по срокам с учетом увеличени€ расходов и воздействи€ на продолжительность проекта. “акого рода анализ можно провести с помощью сетевых графиков;
- дл€ того чтобы более реалистично оценить проект, анализируетс€ возможный диапазон продолжительности каждого действи€, такой анализ проводитс€ методом PERT, который заключаетс€ в веро€тностной оценке проекта.
ѕрименение компьютерных систем при составлении сетевых графиков и проведении соответствующего анализа способствует повышению уровн€ возможной сложности при рассмотрении конкретных проектов.
Ѕольшинство программ способны планировать графики дл€ больших (до 1000 работ) проектов со многими ресурсами. Ёти программы включают, как правило, средства дл€ расчленени€ работ, составлени€ расписани€ в пределах допустимого колебани€ уровн€ ресурсов, учета стоимости работ, различные средства составлени€ отчетов, несколько эвристических правил упор€дочени€ и выравнивани€ ресурсов. Ќаиболее распространены такие специализированные пакеты управлени€ проектами как Project Expert и MS Project, кроме того, в больших системах управлени€, типа ERP-систем существуют специальные блоки, позвол€ющие управл€ть проектами; можно использовать возможности электронных таблиц. Ќиже, в гл. 9 мы подробнее рассмотрим возможности упом€нутых прикладных програм
ƒата добавлени€: 2015-08-26; просмотров: 1219;
