Использование математического аппарата производственных функций при управлении инновациями
Основной функцией руководителя проекта является оперативное руководство работами на всех стадиях жизненного цикла проекта, в том числе на стадии планирования и собственно реализации проекта. Оперативное руководство - это процесс принятия таких решений, в результате которых затраты на осуществление проекта не превышают плановых лимитов, т.е. оперативное руководство состоит из оценки степени технической готовности работ над проектом и корректировки отклонений от планового графика.
На практике функцию оперативного руководства не следует отделять от функции планирования, поскольку оперативное руководство уже предполагает существование некоторого плана, который служит эталоном для измерения и оценки степени продвижения работ. Кроме того, в процессе управления используется сравнение первоначального плана с рядом работ, что позволяет вносить соответствующие коррективы в планы. Таким образом, планирование, оперативное управление и корректировка плана являются взаимосвязанными операциями, выполнение которых постоянно вменяется в обязанности руководителя проекта.
Производственные функции (ПФ) могут служить инструментом, позволяющим проводить разнообразные аналитические расчеты, определять эффективность использования и маневра ресурсов, целесообразность их дополнительного вовлечения в реализацию проектов, планировать выпуск продукции и контролировать реальность планов. Важную роль играют ПФ и в качественном исследовании технико-экономических систем, являясь неотъемлемой частью большинства комплексных моделей экономической динамики, к которым, в первую очередь, относятся различные модели МОБ.
В основе концепции ПФ лежат два принципа моделирования: целевая направленность и аппроксимационный характер модели.
Принцип целенаправленности моделирования состоит в последовательном использовании информации о цели построения модели и сфере ее применения практически на всех этапах построения ПФ - от формирования информационной базы до вычислительных методов оценки параметров. Поскольку цели моделирования могут быть различными, в качестве моделей одного и того же процесса могут использоваться разные ПФ.
Согласно аппроксимационному принципу каждая экономико-статистическая модель рассматривается как звено в системе аппроксимации - процесса последовательного, приближенного и все более точного описания реального явления. ПФ конкретного объекта при таком подходе - результат поиска наиболее адекватного в данных условиях математического описания процесса производства в конкретной экономической системе. При этом условия построения ПФ включают имеющуюся в данный момент информацию о характере функционирования производства, целях и доступных средствах моделирования.
Таким образом, производственной функцией называется аналитическое соотношение, связывающее переменные величины затрат (факторов, ресурсов) с величиной выпуска продукции.
С помощью ПФ решаются задачи:
1. Оценки отдачи ресурсов в производственном процессе;
2. Прогнозирования экономического роста;
3. Разработки вариантов плана развития производства;
4. Оптимизации функционирования хозяйственной единицы при условии заданного критерия и ограничений по ресурсам.
Общий вид ПФ:
Y =Y(R1, R2, …., Ri,…, Rn), (1)
где Y – показатель, характеризующий результаты производства; Ri факторный показатель i-го производственного ресурса; n – количество факторных показателей.
ПФ определяются двумя группами предположений: математических и экономических.
Математически предполагается, что ПФ должна быть непрерывной и дважды дифференцируемой.
Экономические предположения состоят в следующем.
При отсутствии хотя бы одного производственного ресурса производство невозможно, т.е. выполняется:
Y(0,R2,…,Ri,…,Rn) = … = Y(R1,R2,…,Ri,…,0) = … = Y(R1,R2,…, Ri,…,0) = 0; (2)
Рост использования ресурсов приводит к росту результата производства, т.е. выполняются соотношения:
dY/dRi>0, i =1,…,n; (3)
Увеличение затрат одного ресурса приводит к снижению эффективности его использования:
d2Y/dRi2<0, i = 1,…,n. (4)
При макроэкономическом моделировании часто используется предположение о том, что:
Y(lR1,lR2,…,lRi,…,lRn) = lY(R1,R2,…,Ri,…,Rn), при l>0, (5)
где l - постоянная, т.е. о пропорциональности роста результата росту затрат ресурсов.
При условии выполнения сделанных предположений график двухфакторной ПФ Y(X1, X2) имеет вид, представленный на рис.31.
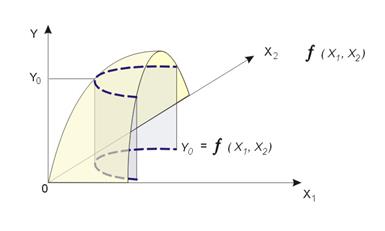
Рис.31. График производственной функции
В табл. 30 дан перечень наиболее известных классов функций. При этом для простоты приведены лишь их двухфакторные записи, т.е. только для n = 2.
Таблица 30. Виды производственных функций
| Название ПФ | Двухфакторная ПФ | Использование |
| 1.Функция с фиксированными пропорциями факторов (ПФ Леонтьева) | Y = min (x1/a1, x2/a2) | Предназначена для моделирования строго детерминированных технологий, не допускающих отклонения от технологических норм использования ресурсов на единицу продукции. Обычно используются для описания мелкомасштабных или полностью автоматизированных производственных объектов |
| 2. ПФ Кобба-Дугласа | Y = a0x1a1x2a2 | Используется для описания среднемасштабных объектов (от промышленного объединения до отрасли), характеризующихся устойчивым, стабильным функционированием |
| 3. Линейная ПФ | Y = a1x1+ a2x2 | Применяется для моделировании крупномасштабных систем (крупная отрасль, н-х в целом), в которых выпуск продукции является результатом одновременного функционирования множества различных технологий |
| 4. ПФ Аллена | Y = a0x1x2 – a1x12 – a2x22 | Предназначена для описания производственных процессов, в которых чрезмерный рост любого из факторов оказывает отрицательное влияние на объем выпуска. Обычно используется для описания мелкомасштабных ПС с ограниченными возможностями переработки ресурсов. |
| 5. ПФ постоянной эластичности замены факторов (ПЭЗ или CES) | Y = (a1x1a3+ a3x2a3)a4 | Применяется в случаях, когда отсутствует точная информация об уровне взаимозаменяемости производственных факторов и есть основания предполагать, что этот уровень существенно не изменяется при изменении объемов вовлекаемых ресурсов. Может быть использована (при наличии средств оценивания параметров) для моделирования систем любого уровня |
| 6. ПФ с линейной эластичностью замены факторов (LES) | Y = x1a0(a1x1 + a2x2)a3 | Рекомендуется для описания производственных процессов, у которых возможность замещения вовлекаемых факторов существенно зависит от их пропорций |
| 7. Функция Солоу | Y = (a1x1a3+ a2x2a4)a5 | Может использоваться примерно в тех же ситуациях, что и ПФ ПЭЗ, однако предпосылки, лежащие в ее основе, слабее предпосылок ПЭЗ. Рекомендуется в тех случаях, когда предположение об однородности представляется неоправданным. Может моделировать системы любого масштаба |
| 8. Ограниченная функция ПЭЗ | Y = min (x1/a1, x2/a2, (a3x1a5 + a4x2a5)a6 | Предназначена для описания двухрежимного производственного процесса, в котором один из режимов характеризуется отсутствием заменяемости факторов, другой – ненулевой постоянной (но не известной заранее) величиной эластичности заменыАналогично – ограниченные функции Л-Д, Солоу и др. |
| 9. Многорежимная функция | Y = (a11x1a0 + a21x2a0)a1 … (a1kx1a0 + a2kx2a0)ak | Используется при описании процессов, в которых уровень отдачи каждой новой единицы ресурса скачкообразно меняется в зависимости от соотношения факторов. Целесообразно применять при наличии априорной информации о числе режимов, а иногда и о ширине «переходной» области между режимами |
| 10. ПФ Линейного Программирования | Y = min (x1/a11, x2/a12) + … + min (x1/ak1, x2/ak2) | Имеет смысл использовать в тех случаях, когда выпуск продукции является результатом одновременного функционирования k фиксированных технологий, использующих одни и те же ресурсы |
Приведем графики некоторых наиболее часто используемых в практике управления ИП производственных функций.
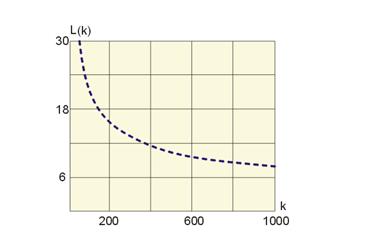
Рис.31. Функция с фиксированными пропорциями факторов (ПФ Леонтьева)
Y = min (L/a1, K/a2)
Такая модель отражает тот факт, что ресурсы не могут заменять друг друга. Если один из ресурсов ограничен, можно рассчитать оптимальный (наименьший) требуемый объем второго ресурса.
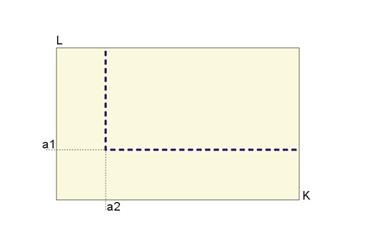
Рис. 32. Производственная функция Кобба-Дугласа Y = a0LaK1-a
Для получения требуемого выпуска можно выбрать соотношение затрат ресурсов L и K.
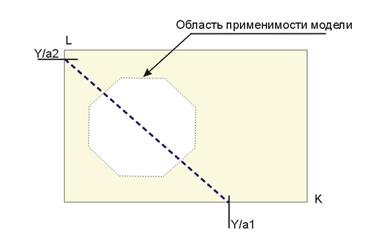
Рис. 33. Линейная производственная функция Y =a1L+ a2K
Модель используется при взаимозаменяемости ресурсов.
На практике ПФ строятся на основе изучения конкретного производственного процесса или процесса реализации ИП. При этом, прежде всего определяется вид аналитического выражения для функции, а затем методами математической статистики - численные значения параметров. Чаще всего используются линейные ПФ вида
m
¦(x) = å aixi,
i=1
а также степенные функции
m
¦(x) = AÕ xaii,
i=1
для которых проблема оценивания параметров сводится к линейной задаче путем перехода к ней логарифмированием функции.
ПФ по существу представляет собой факторное разложение одного из обобщающих показателей – объема выпуска продукции. Построение этой функции дает возможность проводить анализ и оценку влияния факторов на динамику объема выпуска за определенный период. Рассмотрим этапы построения ПФ для предприятия, реализующего ИП.
Пусть задана ПФ для предприятия ¦(x1, ... , xm). Однородная продукция может производиться различными производственными способами, различающимися между собой эффективностью использования ресурсов - разнообразных материалов, затрат труда рабочих разных профессий и т.п.
Каждый производственный способ в пределах рассматриваемого периода (года) обладает фиксированной производственной мощностью, т.е. максимально возможным объемом выпуска.
Обозначим:
yj - количество товара, производимое j-м производственным способом, j = 1,...,n;
mj - производственная мощность j-го способа (ед.тов./год);
xij - удельные затраты i-го ресурса на единицу товара, производимого j-м производственным способом (ед.рес. i/ед.тов.);
wi - стоимость единицы i-го ресурса (руб./ед.рес.), i = 1,...,m;
w0 - объем фиксированных затрат по обслуживанию производства и управлению (руб./год).
Задача определения объема выпуска различными производственными способами, обеспечивающими достижение максимальной прибыли, имеет вид:
n m n
Påyj - [å wi å xijyj + w0] ® max xj. (6)
j=1 i=1 j=1
Максимизация осуществляется по производственным способам. Используя ПФ, выражение (6) преобразуем следующим образом:
m n
P¦(x1, ... , xm) - [ å wi å xijyj + w0] ® max xj, (7)
i=1 j=1
или
n
¦(x1, ... , xm) = max å yj, (8)
j=1
при ограничениях на ресурсы и производственную мощность:
n
å xijyj £ ai, i = 1, ..., m,
j=1
yj £ mj, j = 1, ..., n.
Условие (7) максимизирует прибыль, условие (8) - объем производства по производственным способам.
Подставив выражение (7) в виде
m
P¦(x1, ... , xm) - [å wixi + w0] ® max xj, (9)
i=1
получим модель, в которой максимизация прибыли осуществляется по объемам вовлекаемых в производство ресурсов xj - переменным производственным факторам. Постоянные факторы w0 неизменны. Их наиболее эффективное использование уже отражено в ПФ. Для случая нелинейной ПФ решение задачи (9) определяется совокупностью уравнений
P¶¦/¶xi = wi, i= 1, ..., m, (10)
где слева стоит доход предприятия от применения i-го фактора при фиксированных количествах прочих факторов, справа - цена i-го фактора.
Уравнение (10) отражает принцип вовлечения факторов предприятием, максимизирующим прибыль: оно до тех пор увеличивает количество используемого фактора, пока прирост дохода от дополнительной единицы факторов не сравняется с его ценой, при прочих равных условиях.
Поскольку ПФ представляет собой наиболее обобщенную модель функционирования экономического объекта, ее можно использовать для сравнения работы различных объектов. Обычно сравнение работы двух предприятий за период базируется на попарном сопоставлении показателей производительности труда, фондоотдачи, оборачиваемости оборотных средств, материалоемкости. Показатель сравнительной экономии ресурса x на предприятии Б по сравнению с предприятием А за один и тот же период (или на одном предприятии за разные периоды) вычисляется по формуле:
Э(x) = xА´YБ/YА - xБ, (11)
где xА, xБ - количество используемого ресурса на предприятиях А и Б;
YА, YБ - соответствующие объемы выпуска продукции.
Уменьшаемое в этой формуле показывает количество ресурса x, необходимое для производства продукции YБ на предприятии Б при условии, что ресурсоемкость производства на предприятиях А и Б одинакова. Вычитаемое выражает количество ресурса, необходимое для производства продукции YБ в условиях производства на предприятии Б. Если Э > 0, то эффективность использования ресурса x на предприятии Б выше, чем на предприятии А.
Формула построена на сравнении реальной ситуации на предприятии Б с условной ситуацией, когда “технология” предприятия А переносится на предприятие Б. Понятие “технология” при этом фактически сводится к ресурсоемкости. Эта формула может быть получена из факторного разложения величины xА - xБ на сумму двух слагаемых:
xА - xБ = [ xА´YБ/YА - xБ] + [xА - xА´YБ/YА], (12)
первое из которых выражает вклад в xА - xБ изменения ресурсоемкости продукции, второе - вклад изменения объема выпуска. Здесь используется тождество x = yx/y и предполагается следующая условная последовательность от ситуации предприятия А к ситуации предприятия Б: сначала ресурсоемкость при постоянном выпуске изменяется от xБ/YБ до xА/YА, затем объем выпуска при постоянной ресурсоемкости - от YБ до YА. Поскольку данные для обоснования последнего предположения, так же, как и для обратной последовательности, обычно отсутствуют, интегральный метод рекомендует вместо формулы (11) более сбалансированную формулу для экономии ресурса x:
Э(x) = 1/2[(xА´YБ/YА - xБ) + (xА - xБ´YА/YБ)]. (13)
Эта формула, однако, тоже не может использоваться в большинстве случаев для сравнения эффективности работы двух предприятий, поскольку в ней фигурирует лишь один вид ресурсов. Часто бывает так, что производительность труда выше на одном предприятии, а фондоотдача - на другом. В таких случаях необходим показатель совокупной эффективности использования основных производственных ресурсов.
Для получения такого показателя рассмотрим вместо факторного разложения прироста (экономии) ресурса xА - xБ аналогичное разложение прироста объема производства YБ - YА. Согласно интегральному методу это разложение имеет вид:
YБ - YА = 1/2[(xА´YБ/xБ - YА) + (YБ - xБ´YА/xА)] + 1/2[(xБ´YА/xА - YА) + (YБ - xА´YБ/xБ)], (14)
где первое слагаемое выражает вклад в YБ - YА изменения ресурсоотдачи. По сути дела суммируются результаты сравнения использования ресурсов xА в технологии предприятия Б и ресурсов xБ в технологии предприятия А. Технология в данном случае характеризуется показателем ресурсоотдачи.
Выражение Э = 1/2(xАYБ/xБ - YА + xБYА/xА) допускает обобщение на случай нескольких ресурсов. Пусть xА,Б = (x1А,Б, ... , xnА,Б) - вектор ресурсов предприятий А и Б, ¦А,Б(x) = ¦А,Б(x1, ... , xn) - их ПФ с областями определения МА и МБ, причем xА, xБ принадлежат этим областям. Сравнительная эффективность совокупного использования ресурсов в этих условиях оценивается по формуле:
Эф = 1/2[¦Б(xА) - YА + YБ - ¦А(xБ)]. (15)
Проблема сравнения эффективности различных технологий в общем случае решается путем анализа индексов - измерителей технологической эффективности. Разработка и расчет конкретных значений этих индексов обычно основаны на сопоставлении векторов затрат производственных факторов и конечных результатов производства в натуральном или стоимостном выражении за некоторый определенный период.
В качестве примера рассмотрим построение и исследование модели развития инжиниринговых систем с использованием ПФ //.
Целью исследования региональных инновационных фирм (РИФ) является выявление закономерностей их развития для разработки стратегий управления их функционированием в интересах региона.
На рис. 34. приведена схема управления развитием РИФ. Элемент системы (ЭС) представляет собою инжиниринговую фирму, функционирование которой описывается вектором показателей уr, вектором управления ur и вектором возмущения ¦ ={¦A, ¦}, который представлен в виде двух компонент: ¦ - вектор внешних возмущений, действующих на систему, и ¦A - вектор внешних возмущений, связанных с управленческой деятельностью администрации региона. Поведение администрации описано следующими показателями: yp - показатель развития региона; ¦R - внешние воздействия на регион; uA - управление воздействием на регион, выработанное администрацией.
Объектом изучения является элемент системы, который функционирует в определенной социально-экономической среде. Его развитие происходит в соответствии с собственными интересами, которые в общем случае противоречат целям региона. Задачей администрации, которая представляет интересы региона, является обеспечение условий, в которых цели региона и отдельного объекта совпадают. Причем, в условиях рыночной экономики, такое управление должно быть не директивным, а ситуационным. Администрация должна создавать условия (ситуацию), в которых поведение элементов соответствует целям региона в целом. Общая схема задачи управления может быть сформулирована следующим образом.
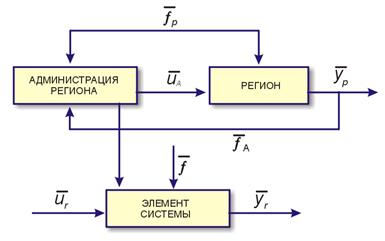
Рис. 34. Структура управления развитием РИФ.
Возможны две постановки задачи оптимального управления:
1. При "пассивной" стратегии администрации.
2. При "активной" стратегии администрации.
Предполагается, что руководство ЭС всегда ищет оптимальную стратегию своего развития, руководствуясь своими критериями. При первой постановке задачи компоненты вектора ¦А заранее определены и известны. Во втором случае компоненты ¦A могут меняться в соответствии с замыслами администрации Рассмотрим задачу стратегического управления развитием фирмы. Для построения концептуальной модели процесса развития необходимо выделить минимально необходимый набор управляемых, изменяемых в определенных пределах факторов, показателей и связей, наиболее существенно влияющих на получение желаемых конечных результатов.
Объектом моделирования является самостоятельное звено системы регионального инжиниринга - инжиниринговая фирма в современных рыночных условиях.
Модель должна учитывать, как минимум, следующие группы показателей, описывающих: результаты, ресурсы, производство, средства развития, экономику и финансы, управляющие воздействия, оценку эффективности ЭС.
Будем считать, что конечные результаты описываются следующими группами показателей: выпуск продукции и услуг (в стоимостном выражении), среднее потребление и прибыль.
Средствами развития являются производство, дающее основной вклад в развитие мощностей (производственных фондов) и их структуры, и научно-технический прогресс, дающий основной вклад в изменение удельных показателей эффективности.
Главным фактором, определяющим конкурентоспособность ЭС во внешнем мире и возможность интенсивного развития при ограниченных ресурсах, является эффективность.
Её показатель определяется отношением результата (выхода) к ресурсам (входу). Это такие внешние показатели как:
1) интегральный показатель - (а) средний показатель (отношение выпуска к затратам и, наоборот, затрат к выпуску); (б) индекс прироста эффективности - отношение индекса прироста выпуска (дохода) к суммарному приросту ресурсов;
2) материалоемкость;
3) производительность труда;
4) фондоотдача и ряд других (рентабельность и др.).
Выбор оптимальной стратегии управления развитием фирмы, занимающейся наукоемким производством, заключается в определении параметров математической модели, а именно оптимальной доли потребления и доли отчислений на развитие инструментально-кадровой среды.
Проведем анализ данных, характеризующих финансово-экономическую деятельность предприятия в период с 1992 по 1996 годы (в качестве примера рассматривалась деятельность региональных инжиниринговых фирм в социально-экономических условиях Оренбургской области и сложившаяся система инжиниринга в области в целом). Определим параметры производственной функции, необходимые для построения математической модели.
Будем использовать производственную функцию вида:
Y = aFaL1-a,
где Y, F и L - годовой оборот фирмы, стоимость основных фондов и количество трудовых ресурсов, соответственно;
а и a - параметры производственной функции, подлежащие определению.
Результатом исследований является анализ влияния стоимости основных фондов и трудовых ресурсов на годовой оборот фирмы.
Производственная функция, описывающая динамику развития инжиниринговых фирм, имеет следующий вид:
Y =1864208 F0'270002 L1-0.270002
Результаты аппроксимации значений Y приведены на рис. 35, где Ym - значение годового оборота, найденного по формуле (2); Yr - реальное значение этого показателя.
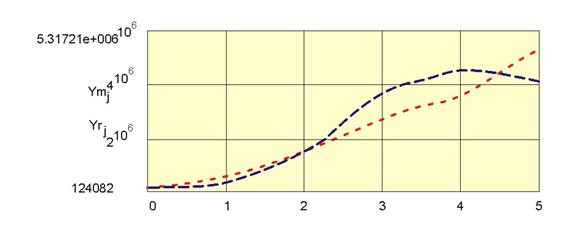
Рис. 35. Графическое представление результатов аппроксимации производственной функции
В процессе вычислений использованы следующие значения параметров:
-темп выбытия трудовых ресурсов q1 = 0.2/12 (в месяц);
- коэффициент выбытия основных фондов q2 = 0.2/12 (в месяц);
- коэффициент амортизации m = 0.14/ 12 (в месяц);
- начальное количество производственных фондов Fo= 60 млн.р.;
- первоначальный уровень трудовых ресурсов Lo= 3 чел.;
- ставка заработной платы s = 1 млн р.
Как было указано выше целесообразно рассмотреть два варианта развития системы:
1. при пассивной стратегии управления регионом;
2. при активной стратегии регионального управления.
В первом случае задача сводится к следующей.
Задача I.
На каждом этапе развития (Dt = 1 мес.) необходимо найти оптимальные значения управляющих параметров g - доля отчислений на развитие основных фондов и u - доля отчисления из дохода на потребление такие, чтобы максимизировать удельное потребление системы, при условии, что объем выпускаемой продукции не уменьшается.
В результате проведенных вычислений в среде Mathcad при такой постановке задачи система обеспечивает высокое качество развития при выборе управляющих параметров, равными u = 0.95 и g = 0.95. Основные производственные показатели: трудовые ресурсы Lotn, основные производственные фонды Роtn, доход Dotn равномерно растут примерно с одинаковым темпом около 4% за год (рис. 36). Протяженность траектории - 3 года (36 месяцев).
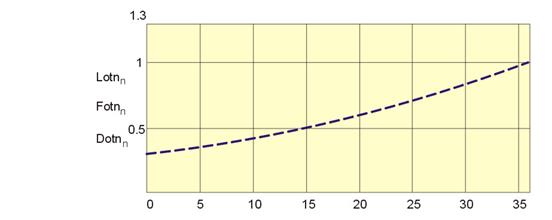
Рис. 36. Динамика развития основных производственных параметров
Дата добавления: 2015-08-26; просмотров: 1632;
