Теорема Гаусса в дифференциальной форме. Чтобы получить выражение для дивергенции поля Е, над взять бесконечно малый объем V, определить по­ток вектора Е сквозь замкнутую поверхность

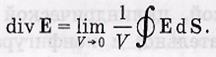
Чтобы получить выражение для дивергенции поля Е, над взять бесконечно малый объем V, определить по­ток вектора Е сквозь замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему.

В декартовой системе координат

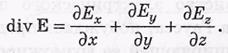
Дивергенция поля Е связана с плотностью заряда ρ в той же точке уравнением

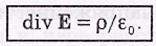
Векторный дифференциальный опера­тор 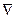(«набла»). В декартовых координатах он имеет вид

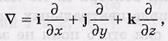
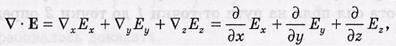Имеет смысл только в сочетании со скалярной или векторной функцией, на которую символически умножа­ется.

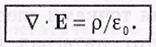это div E. Теорема Гаусса в операторной форме имеет вид

Теорема о циркуляции вектора Е.

Электростатическое поле — поле, образованное системой неподвижных зарядов является консерва­тивным, т. е. работа сил этого поля не зависит от пути, а за­висит только от положения начальной и конечной точки. Именно таким свойством обладает Элементарная работа сил поля на перемещение пробного положительного заряда из точки 1 заданного поля Е в точку 2 на пути dl равна Е dl, a вся работа сил поля на пути от точки 1 до точки 2 определяет­ся как

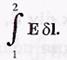
Этот интеграл берется по некоторой линии (пути), поэтому его называют линейным. Интеграл по замкнутому пути называют циркуляцией вектора Е. По произволь­ному замкнутому пути этот интеграл равен нулю.

Циркуляция вектора Е в любом электростатическом поле равна нулю, т. е.

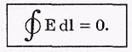
(теорема о циркуляции векто­ра Е.)

Работа сил поля при перемещении единичного положи­тельного заряда из точки 1 в точку 2, не зависит от пути между этими точками и равна

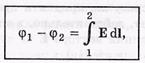
где φ₁ и φ₂ — значения функции φ в точках 1 и 2. Эта величина φ(r) называется потенциалом поля. Работа сил потенциального поля равна убыли потенциальной энергии частицы в поле,а потенциал — это величина, численно равная потенциальной энергии еди­ничного положительного заряда в данной точке поля.

Элементарная убыль потенциала на этом перемеще­нии есть

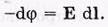
Потенциал поля неподвижного точеч­ного заряда:

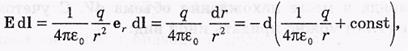интегрируя ,получаем потенциал поля точечного заряда

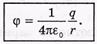
Потенциал системы неподвижных точечных зарядов

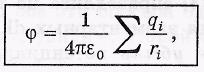
r_i — расстояние от точечного заряда q_i до интересующей точки поля.

Если заряды, образующие систему, распределены непрерывно, то

.

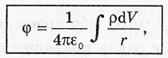
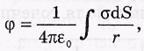Если заряды расположены только на поверхности S, то

Связь между потенциалом и вектором Е

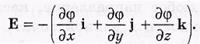
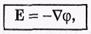Величина, в скобках это градиент потенциала φ (grad φ или ).

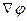т. е. напряженность Е поля равна со знаком минус градиенту потенциала.

Эквипотенциальные поверхности.

Эквипо­тенциальной поверхности -поверхности, во всех точках которой потенциал φ имеет одно и то же значение. Там, где эти поверхно­сти расположены гуще («круче потенциальный рельеф»), там напряженность поля больше.

Вектор Е всюду нормален к эквипотен­циальной поверхности, линии вектора Е ортогональны этим поверхностям.

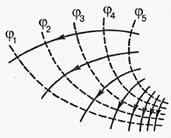
Пунктиром показаны — эквипотенциали, сплошными линиями — линии вектора Е.

Электрический диполь.Поле диполя.

Электрический диполь — это система из двух одинаковых по модулю разноименных точечных зарядов + q и— q, находящихся на некотором расстоянии lдруг от друга.

Потенциал поля диполя в точке Р (рис.а)

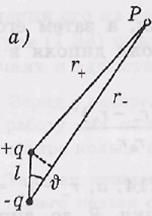
определяется как

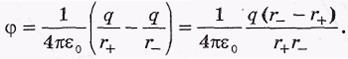
r>>l , r_- - r₊ = lcosθ , r_- ∙ r₊=r²

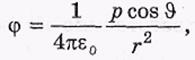
где р = ql — электрический момент диполя - вектор, направленный по оси диполя от отрица­тельного заряда к положительному:

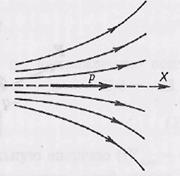
Поле диполя

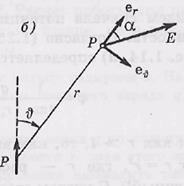Проекции вектора Е на два взаимно перпендикулярных направления — вдоль ортов e_r и e_θ (рис. б):

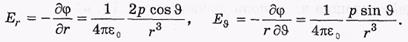
модуль вектора Е

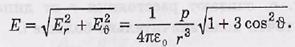
Сила, действующая на диполь, во внешнем неоднородном электрическом поле

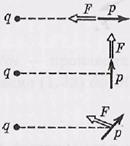
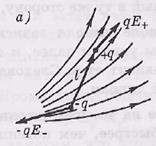Результирующая сила F, действующая на диполь, равна (рис. а):

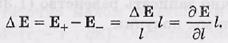
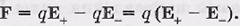или

В общем виде формула для силы, действующей на диполь в неоднородном электрическом поле:

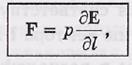
Момент сил, действующих на диполь.

,

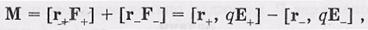
. При достаточно малом расстоянии между зарядами диполя

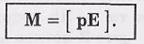
Этот момент сил стремится повернуть диполь так, чтобы его электрический момент р установился по направлению внешне­го поля Е. Такое положение диполя является устойчивым.

Энергия диполя в поле.

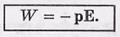
Диэлектрики.Поляризация диэлектрика

Диэлектриками