Задача 2.1-10

Определить абсолютное давление на поверхности жидкости в сосуде и высоту h, если атмосферное давление равняется 740 мм.рт.ст. Поддерживающая сила F = 10 H, вес сосуда G = 2 Н, его диаметр d = d_н мм. Толщиной стенки сосуда пренебречь.

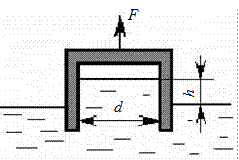
Рис. 2.8. К задаче 2.1-10

2.1.1. Дифференциальное уравнение равновесия жидкости.
Поверхность равного давления

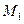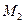Предположим, что в точке М находится объем жидкости dV (см. рис. 2.9). На него воздействуют силы давления соседних объемов. Определим результирующую силу давления на объем dV. dV расположен параллельно осям координат, da, db, dc – его стороны. В точке М давление обозначим как p. В точках и , принадлежащих сторонам параллельным плоскости x0y давление будет соответственно 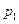и . Если рассматривать одну из сторон параллелепипеда, то результирующая сила давления на эту сторону действует по нормали к ней и ориентирована внутрь объема dV.

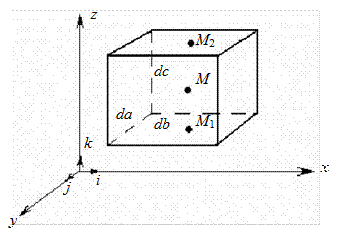
Рис. 2.9. Объем жидкости, находящийся в равновесии

Для результирующей силы сторон объема dV, параллельных плоскости x0y можно записать

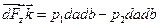или ,

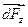параллельна оси 0z.

Разность 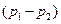можно записать в виде 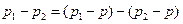, но в соответствии со свойством градиента давления можно написать

, ,

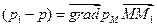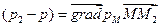откуда .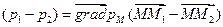

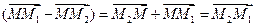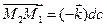Так как и , то

.

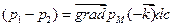Таким образом, результирующая сила 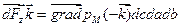, но dcdadb = dV,oткуда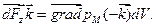

Аналогичные результаты мы получим для сил 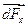и .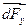

Результирующая всех сил, действующих на объем dV будет соответственно

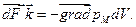
(2.1)

Выводы:

1. Результирующая сила 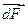направлена в противоположную сторону, чем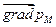

2. 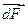перпендикулярна плоскости, проходящей через точку М, на которой давления одинаковы и ориентирована в сторону уменьшения давления.

В жидкости, находящейся в покое, действуют:

– сила тяжести

,

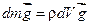направленная вертикально вниз;

– равнодействующая сила давления

,

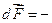
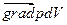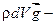
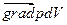= 0

или .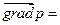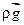

(2.2)

Выводы:

1. Вектор градиента давления направлен вертикально вниз, как и вектор .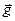

2. В жидкости, находящейся в равновесии давление увеличивается сверху вниз.

3. В покоящейся жидкости плоскости равного давления горизонтальны.

4. В покоящейся жидкости давление в точке зависит только от ординаты z.

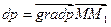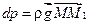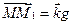Т.к. , то с учетом полученного уравнения, можно записать . Т.к. и , то

.

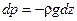(2.3)

Нами получено основное уравнение гидростатики в дифференциальной форме.