Аналитическое счисление

Аналитический способ счисления (его еще называют письменным счислением) применяется в тех случаях, когда графическое счисление невозможно или когда оно сопровождается значительными графическими погрешностями.

Формулы аналитического счисления являются основой алгоритмов автоматизированного счисления.

Аналитическим счислением называется вычисление приращений к исходным координатам, обусловленным движением судна, с помощью которых определяются счислимые координаты на заданный момент времени. Аналитическое счисление применяется при плавании вдали от берегов, использовании мелкомасштабных навигационных карт, расчетах счислимых широты и долготы при решении астрономических задач и, наконец, формулы аналитического счисления заложены во все автоматические счислители координат и путепрокладчики.

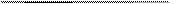
P_N a¹ dw

b¹

РД B b)

а) dj

a¹ b¹ К ds

К S

A dS A

Обратимся к элементарному треугольнику А а¹ b¹(Рис.1.38b), считая Землю за сферу.

Здесь: А а¹ = dj,

b¹ a¹ = dl Cosj = dw

A b¹ = dS

Если принять этот треугольник за плоский,то можно записать дифференциальные уравнения:

dj = dS CosK и dl Cosj = dSSinK

В результате интегрирования при K = Const получим:

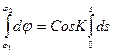j₂ - j₁ = S CosK или

РШ = S CosK (1.55)

Для интегрирования dlCosj значение Cosj относят к параллели промежуточной широты, и выносят за знак интеграла:

Cosj_n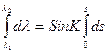

(l₂ - l₁)Cosj_n = S SinK или

ОТШ = S SinK (1.56)

Геометрический смысл состоит в том, что ОТШ представляет собой длину отрезка параллели некоторой промежуточной широты j_n, заключенной между меридианами

(l₁ l₂), а единица измерения морская миля, но не экваториальная минута.

Для вычисления РД воспользуемся соотношением, выражающим длину дуги экватора и параллели.

.

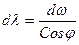Умножим числитель и знаменатель этого выражения на dj.

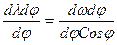
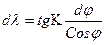
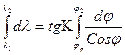
Теперь, исходя из свойства навигационной карты, можно записать:

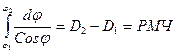, откуда

РД = РМЧ tgK, (1.57)

в тоже время

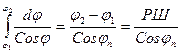
После искусственных преобразований получим:

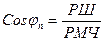или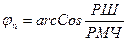

Для практических задач при небольшом (коротком) пройденном пути можно принять, что Cosj изменяется линейно и (в высоких широтах при Dl ³ 10,0° погрешность вычисления долготы будет ощутимой до 2% от Dl) промежуточная широта приравнивается к средней ,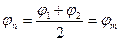

отсюда окончательно получаем выражение для расчетов разности долгот:

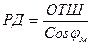(1.58)

Замена j_n на j_m дает погрешность в расчетах РД (D) исходя из формулы: D=ОТШtgj_mSecj_nSin(j_n-j_m).

По приведенным формулам для нахождения РШ, ОТШ и РД составлены таблицы № 24, 25 в Мореходных таблицах МТ=75. Таблица 25б используется при решении задачи с учетом сфероидичности Земли. В рассчитанные РШ и РД вводят поправки f и g.

Непосредственно по формулам аналитического счисления находят поправки к начальным счислимым координатам j_К = j_Н + Dj и l_К = l_Н + Dl. Вычисление поправок трудоемко, и для расчетов используют ЭВМ.

Аналитический способ расчетов координат намного точнее графического, так как позволяет применять точные формулы сферической тригонометрии и учитывать сфероидичность Земли. Этот способ используется при определении места судна по гиперболическим РНС и спутниковым СРНС.

Аналитическое счисление принято подразделять на три вида: простое, составное и сложное.

Простое аналитическое счисление

Выполняется, когда судно следует одним курсом и нужно найти координаты конечной точки или по координатам начальной и конечной точек рассчитать Курс (К) и плавание на этом курсе (S). По начальным координатам (j₁ l₁ ), курсу (К) и плаванию (S) находят РШ, ОТШ и затем РД и получают значения координат конечной точки j₂ = j₁ +РШ l₂ = l₁ + РД.

Решение задачи по вычислению курса (К) и плавания (пройденного расстояния) (S) по известным координатам точек отшествия и пришествия можно выполнить по формулам:

tgK = 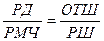S = РШ CosecK

Составное аналитическое счисление.

При составном счислении (Рис.1.39) вычислят координаты точки пришествия, если судно плавало несколькими курсами.

Для нахождения координат точки пришествия (Е) рассчитывают РШ и ОТШ для каждого курса, а затем вычисляют (РШ и ОТШ в этом случае называются генеральными ГенРШ и ГенОТШ):

ГенРШ = åРШ_N(S) + åРШ_S(N)

ГенОТШ = åОТШ_E(W) + åОТШ_W(E).

Nи

С

В ОТШ РШ

ОТШ

РШ D

РШ

А

Рис.1.39 Е

Имея суммы РШ и ОТШ, находим широту точки пришествия (j₂) среднюю широту (j_М):

j₂ = j₁ + ГенРШ, j_М = .или +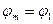

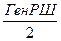
После чего вычисляем долготу точки пришествия:

РД = 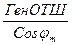, l₂ = l₁ + РД

При обратной задаче, известны:

- разность широт РШ

- отшествие ОТШ

Вычисляют генеральный курс (K) (между точками АЕ) и плавание (S) отрезок АЕ.

tgK_Г = 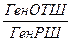, tgK_Г = 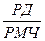, S = ГенРШ CosecK_Г

В составном счислении можно учитывать течение и циркуляцию.

При учете течения принимают курс как направление действия течения (К_Т), а плавание - как произведение времени на скорость течения. Время воздействия течения на судно рассчитывается, исходя из конкретных условий плавания.

(S_Т = DТ*V_Т).

При аналитическом счислении циркуляция учитывается по ИКср и плаванию по нему d.

Сложное счисление.

В этом методе аналитического счисления, кроме расчетов РШ и ОТШ на каждом курсе, вычисляются и координаты конечных точек.

Когда аналитическое счисление производится на вычислительных устройствах, сопряженных с указателями курса и скорости, счислимые координаты рассчитываются непрерывно.

В вычислители вводятся математические выражения, позволяющие учитывать сфероидичность Земли.

j_i+1 = j_I + 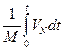; l_i+1 = l_I +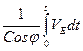

Здесь М и N – главные радиусы кривизны меридианного эллипса, а V_N и V_E – составляющие скоростей по меридиану и параллели соответственно.