Тема 4. Математичні методи прогнозування
4.1. Прогнозна модель, її характеристики і план складання
Моделі, що прогнозують величини техніко – економічного показника, який вивчається, можуть бути трьох видів:
· одночинники, що виражають зміну самого показника;
· парні регресійні, що виражають зміну показника залежно від зміни одного чинника;
· багаточинники, що виражають зміну показника залежно від групи найважливіших, які визначаюють його чинників.
Моделі, за допомогою яких прогнозується зміна тільки самого показника, незалежно від причин, що його (показника) викликають, мало ефективні, особливо для оперативного управління. Вони не дозволяють виявляти напрям і міру дії на певні чинники для досягнення управління показника, заданого на прогнозований період.
Парні регресійні моделі, залежність зміни показників, від єдиного чинника, не враховують всю сукупність найважливіших чинників, а їх взаємодія може призвести до значних спотворень ізольованого впливу облікового чинника.
Досить цінними є прогнозуючі моделі багаточинників, які охоплюють найважливіші чинники, що обумовлюють зміну показника, що вивчається і враховує взаємозв'язок між ними. При цьому особливо важливе включення в модель саме керованих чинників, причому за станом на декілька періодів, передуючих прогнозованому. По кожному чиннику повинен бути виявлений лаг, що вказує тривалість запізнювання найбільшого впливу чинника на показник. За відсутності лага по даному чиннику слід замінювати цей чинник його авторегресійною моделлю. Якщо, наприклад, всіх чинників чотири: чинники 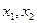 запізнюються з лагом
запізнюються з лагом 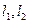 , а чинники
, а чинники 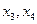 діють синхронно, то модель багаточинника слід будувати у вигляді
діють синхронно, то модель багаточинника слід будувати у вигляді
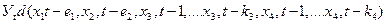 , (4.1)
, (4.1)
де к3 і к4 - число членів авторегресійної моделі для чинників х3 і х4 відповідно.
Така модель дозволяє за умов, досягнутим рівнянням чинниками, намічати заходи впливу на них з тим, щоб в планований період показник досяг даного рівня.
Складання моделей багаточинників включає наступні етапи:
· визначення еволюційних складових для показника Уt і всіх чинників Xjt (j=1,2….p), Уt=d(t) и Xjt =dj(t);
· виявлення лага впливу кожного фактора на показник l1,l2…lp.
· визначення Р - факторної моделі показника виду У=d (X1,t-e1,….Xp,t-ep);
· знаходження авторегресійних моделей для факторів, що діють синхронно (lj=0) Xjt=d(Xj,t-1,Xj,t-2,….Xj,t-k);
· складання багатократної моделі.
Вимога високої точності й достовірності прогнозованої моделі багаточинника викликає необхідність врахування, як специфіки обробки рядів динаміки, так і особливостей багатократної регресії.
Специфіка застосування регресійного аналізу до рядів динаміки досить суттєва, якщо її не враховувати, то це може призвести до серйозних помилок.
Перерахуємо деякі специфічні риси аналізу:
1. При обробці вибіркових даних спостережень, дослідів або звітів, що відносяться до єдиного певного моменту часу, вважається виконаною вимога незалежності випробувань, яка є однією з основних для застосування вірогідних методів. У рядах динаміки ця вимога не виконується, бо при зміні процесу в часі подальші значення ряду динаміки залежать від попередніх.
2. Показники тісноти зв'язку між функціональною ознакою У і деяким чинником Х в звичайній кореляційній моделі так чи інакше враховують частку дисперсії У, обумовленої впливом Х. У рядах динаміки поняття дисперсії втрачає звичайне значення, оскільки при зміні деякої величини в часі дисперсія залежатиме не тільки від випадкових відхилень значень ряду від його середнього значення, але ще і від вибраного для вивчення процесу проміжку часу, тобто довгі ряду.
3. Якщо два тимчасові ряди мають схожі еволюційні складові, наприклад, два монотонно зростаючих тренду, то коефіцієнт кореляції між ними виявиться високим, хоча по суті дані величини можуть не бути абсолютно зв'язані між собою (явище помилкової кореляції).
Першим етапом дослідження повинен бути відбір найважливіших чинників виходячи з економічного змісту процесу.
За показником і вибраними чинниками, що вивчаються, збирають вихідні дані (звітні дані, результати спостережень і дослідів). Рекомендується користуватися даними по одному об'єкту і складати модель тимчасову, а не просторову. При цьому не враховані в моделі чинники коливатимуться значно менше ніж по групі об'єктів, і застосування отриманої моделі для аналізу і управління буде значно точнішим і надійнішим.
Таблиця 4.1 – Матриця статистичних даних економічних показників
| t | Yt | X1t | X2t | .. | Xpt |
| Yt1 | X11 | X21 | .. | Xp1 | |
| Y2 | X12 | X22 | .. | Xp2 | |
| Y3 | X13 | X23 | .. | Xp3 | |
| Y4 | X14 | X24 | .. | Xp4 | |
| . | . | . | . | . | . |
| n | Yn | Xnt | Xnt | .. | Xnt |
Складання прогнозуючої моделі є безперервним процесом: при настанні прогнозованого періоду нові дані дозволяють перевірити і скоректувати раніше отримане рівняння, а після деякого часу визначити нову модель по новому базисному періоду. При цьому слід регулювати терміни оновлення моделі економічно: складати витрати на отримання нової моделі і збитки від похибок прогнозування за старою моделлю.
Дата добавления: 2015-08-26; просмотров: 681;
