Обґрунтування форми зв'язку змінних і розрахунок параметрів теоретичної лінії регресії

Після попередньої обробки статичних даних приступають до складання рівняння регресії У за кожним аргументом Х. Загальна схема послідовних дій полягає в наступному:

- за дослідженими даними складатися кореляційна таблиця і кореляційне поле в звичайній декартовій координатній сітці;

- обчислюються середні 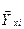і будується емпірична лінія регресії 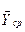по Х_i, що характеризує зміну середнього значення функції під впливом чинника аргументу.

Середні інтервальні значення 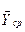визначаються за допомогою співвідношення

. (3.1)

Доцільно використовувати спрощений спосіб обчислень шляхом переходу до нових значень функції

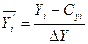, (3.2)

де С_yi – вибраний центр переходу до нових значень. Перетворені змінні переводяться в натуральні:

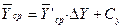, (3.3)

де ΔҮ – величина інтервалу.

Середні інтервальні значення функції 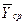відображаються на кореляційному полі у вигляді точок із середини інтервалів зміни Х_i.. Потім ці точки з'єднуються і отримана ламана лінія має назву емпіричної. Її зиґзаґи сильніше виявляються в інтервалах з малою кількістю спостережень. За законом великих чисел можна стверджувати, що емпірична лінія регресії все більше згладжуватиметься при зростанні числа спостережень.

Граничне положення емпіричної лінії регресії, до якого вона прагне при необмеженому збільшенні числа спостережень має назву теоретичної лінії регресії, а процес її знаходження – вирівнюванням емпіричної лінії регресії.

Суттєву роль в кореляційному аналізі відіграє підбір форми математичного рівняння, що найкращим чином описує досліджуваний процес.

Математичні функції 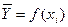для опису залежності можуть бути найрізноманітнішими. Найширше розповсюдження знайшли лінійні рівняння регресії виду

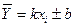. (3.4)

Параметри лінійного рівняння легко визначаються, рівняння зручне в застосуванні, теорія лінійної кореляції вивчена найбільш докладно. Проте лінійна залежність має свої специфічні властивості, які не можуть належати всьому різноманіттю економічних явищ.

Основні властивості лінійної функції:

- швидкість зміни У із зростанням Х постійна, не залежить від величини Х, тобто ;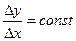

- абсолютні максимум і мінімум У в будь-якому діапазоні зміни Х досягаються на його кінцях.

З цього виходить, по-перше, що різноманітні процеси, швидкість перебігу яких змінна і залежить від досягнутого рівня, тільки грубо приблизно можуть описуватися за допомогою лінійної функції; по-друге, якщо абсолютний максимум або мінімум величину, яка вивчається, досягається всередині даного діапазону зміни Х, то за допомогою лінійної функції він виявлений бути не може. Ця остання обставина особливо суттєва при вирішенні задач оптимізації.

Далі лінійна регресія У по Х припускає виконання наступних строго певних умов:

- дисперсія величини У, відповідна даному значенню Х, постійна, тобто 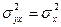, або пропорційна даній функції від Х, тобто .

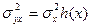Вказані умови на практиці виконуються рідко. Отже складність реальних процесів, нерівномірність їх протікання, наявність екстремальних значень і різнонаправленість дії окремих взаємозв'язаних чинників у більшості випадків не дозволяють достатньо обґрунтовано застосовувати лінійні методи. Це призводить до необхідності розрахунку нелінійних рівнянь.

Виходячи з фізичної, технологічної, економічної сутності дослідженого процесу і враховуючи вид емпіричної лінії регресії, робиться гіпотеза про форму залежності функціональної ознаки У від аргументу Х по суті, забезпечуючи найкраще наближення розрахункових результатів до початкових даних.

Для раціонального вибору форми зв'язку дослідник повинен мати в розпорядженні достатній вибір інструментів для оцінки залежності.

Доцільно користуватися дво- і трипараметричними рівняннями. Для моделювання показників, що монотонно зростають, можна отримати добре наближення двопараметричними значеннями, а моделі трипараметричні при коректному їх підборі виконуються для досить точного опису більшості процесів, що допускають єдиний екстремум. Монотонність або екстремальність залежності повинна бути обумовлена характеристиками процесу і підтверджуватися виглядом емпіричної лінії регресії.

Використання багатопараметричних рівнянь недоцільне, хоча за допомогою максимуму функції можна отримати близьке наближення до початкових даних. Проте таким чином описується не стільки велика тенденція, скільки випадкові відхилення. Такі функції можуть мати максимуми і мінімуми, не виправдані по суті. Крім того, як складання таких функцій, так і їх застосування для практичних розрахунків різко ускладнюється.

Більшість математичних функцій, що використовуються для опису техніко-економічних показників, шляхом функціональних перетворень У по Х (роздільно або одночасно) можуть бути зведені до лінійного вигляду. При цьому метод перетворень залежить від форми зв'язку.

Гіпербола вигляду 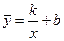перетвориться в лінійну шляхом заміни. Статична функція вигляду 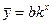перетвориться в лінійну шляхом логарифмуванням. У результаті маємо 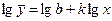. Позначимо .

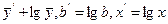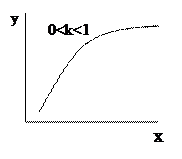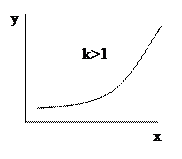У результаті маємо .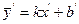

Показова функція виду y=be^kx перетвориться в лінійну логарифмуванням .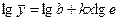

Позначимо 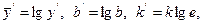при цьому 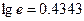. У результаті маємо .

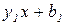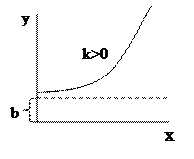Теоретична лінія регресії може бути подана у вигляді плавної кривої яка кількісно виражає зв'язок між середніми інтервальними значеннями 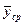і відповідними значеннями Х (аргументами). Процес знаходження невідомих параметрів теоретичної залежності є однією з важливих проблем теорії кореляції і регресії.

Існує кілька способів встановлення аналітичної залежності, точніше, знаходження невідомих параметрів рівняння: графічний, методи середніх, найменших квадратів та інші.

При графічному способі залежність визначають за допомогою лінійки (протягнутої нитки) так, щоб по обох сторонах проведеної потім лінії розташовувалося приблизно однакова кількість точок. Якщо характер розташування точок вказує на наявність криволінійної залежності, то використовується лекало, або шляхом функціональних перетворень змінних нелінійна залежність зводиться до лінійного вигляду.

Числове значення коефіцієнта залежності функції 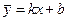визначається за формулою

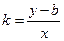, (3.5)

де у і х - похідні числові значення за графіком.

Відшукавши як мінімум дві точки, по них проводять пряму.

Якщо лінійну пряму розташувати так, щоб точки приблизно однаково розташовувалися по обидві сторони від неї, то параметри лінійного рівняння можна визначити з рівняння

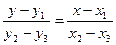, (3.6)

де у₁х₁, у₂х₂ – значення координат двох точок, які найкращим чином "вписуються" у пряму.

Сутність середньоарифметичного способу полягає в знаходженні середньоарифметичного значення від всіх n значень У і Х, а також додаткових середніх для точок, чисельні значення яких менше x_ср.^b і y_ср^b і більше x_ср.^н и y_ср.^н. У цьому випадку сума відхилень відстаней точок по обидві сторони від теоретичної лінії, визначених на осі ординат, дорівнює нулю.

Кутовий коефіцієнт теоретичної лінії знаходять за формулою

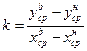, (3.7)

де y_ср.^b, x_ср^b_.- верхня середня (координати точок); y_ср.^н,х_ср.^н - нижня середня.

Значення вільного члена b знаходять за графіком.

Основними недоліками графічного методу визначення математичної залежності слід вважати суб'єктивність «якнайкращого розташування» лінійної прямої. Якщо на тривалість виконання роботи впливають одночасно кілька чинників, то графічний метод можна застосовувати тоді, коли є можливість заздалегідь визначити залежність роздільно по кожному чиннику за умови, що значення решти чинників залишаються постійними.

Для обчислення параметрів рівняння виду 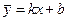частіш за все користуються методом найменших квадратів. При цьому ставиться умова, щоб сума квадратів відхилень (відстаней) всіх досліджених точок від ординат, обчислених за рівнянням прямої ε_i, була мінімальною. Іншими словами, пряма повинна проходити якомога ближче до вершин емпіричної лінії регресії. Це означає, що параметри К і b управління регресії треба визначити з рівняння:

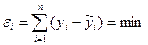, (3.8)

де y_i – ординати досліджуваних точок;

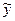_i – ординати розрахункових точок, визначені за рівнянням регресії 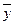=к х_i+ b таким чином .

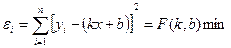Умовою екстремуму даної функції слід вважати рівність нулю часткових виробничих, узятих за параметрами К і b

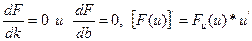звідси 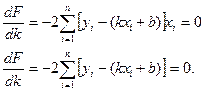(3.9)

Скоротивши на (-2) і розкривши квадратні дужки, отримаємо систему лінійних рівнянь

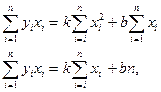(3.10)

підставивши сюди чисельні значення відповідних величин, знайдемо параметри К і b.

У разі лінійної залежності геометричне і алгебраїчне значення коефіцієнта регресії полягає в тому, що він кількісно характеризує на скільки в середньому змінюється у при зміні Хi на одиницю свого вимірювання. Чим більше чисельні значення коефіцієнта регресії, тим більше відносний приріст функції при зміні аргументу.

При знаходженні параметрів параболи виду 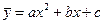необхідно складати і вирішувати систему з трьох нормальних рівнянь, яке розв’язується, виходячи з вимоги методу найменших квадратів, тобто .

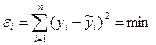Підставляючи 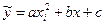, маємо

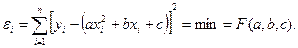(3.11)

Знаходимо часткові похідні 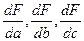і прирівнюємо їх до нуля

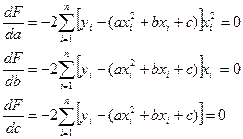(3.12)

Після відповідного перетворення маємо

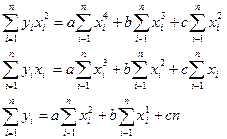(3.13)

Не важко помітити, за яким правилом складається система нормальних рівнянь для знаходження невідомих параметрів шуканої функції.