Оцінка тісноти, суттєвості й лінійності (нелінійності) зв'язку між змінними

Тіснота зв'язку між змінними характеризується ступенем відхилення (розсіяння) досліджуваних точок біля теоретичної лінії регресії. Чим ближче окремі спостереження розташовані до теоретичної лінії регресії, тим більше повна залежність у по х.

Кутовий коефіцієнт лінійного кореляційного зв'язку між у і х, який показує, на скільки одиниць в середньому зміниться функція, якщо аргумент збільшується (зменшується) на одиницю свого вимірювання не може служити показником тісноти зв'язку між змінними. У цьому випадку його чисельне значення залежить від прийнятих одиниць вимірювання змінних.

Для оцінки тісноти зв'язку між змінними використовується емпіричне кореляційне відношення (η²_y/х), яке є часткою дисперсії (коливаємості) функції у за рахунок впливу даного аргументу х. У даному випадку загальна (повна) дисперсія розкладається на дві частини – дисперсію усередині кожного інтервалу зміни функції σ ²_y/х, яка не залежить від впливу Х, і дисперсію середніх значень функції δ 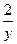, яка викликана впливом аргументу, тобто

σ²_y= σ²_y/х+ δ 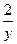. (3.14)

Звідси формула для оцінки тісноти зв'язку між змінними має вигляд

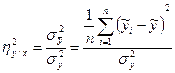, (3.15)

а в разі згрупованих даних

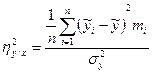, (3.16)

де 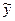_I - розрахункове значення функції;

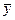- середнє значення функції за вибіркою;

n - обсяг вибірки;

к - кількість інтервалів зміни функції;

m_i – число спостережень у в кожному інтервалі зміни.

Кореляційне відношення не залежить від одиниць вимірювання змінних, що вивчаються. Воно показує, яку частину загальної дисперсії σ²_y можна віднести за рахунок зміни аргументу на одну σ²_х.

При цьому характеристика η²_y/х тим точніше визначає частку впливу Х на загальну дисперсію у, чим менше варіюється залишкова дисперсія σ²_y/х при кожному Х. Якщо η_y/х=1, то має місце функціональна залежність у від х. Якщо η_y/х=0 – у кореляційно не залежить від х.

У разі лінійної залежності змінних дисперсію середніх значень функції можна записати у вигляді

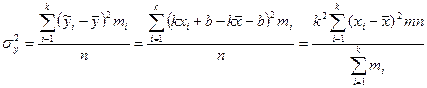(3.17)

Спростивши це відношення:

δ_y²= К² σ²_х. (3.18)

Тоді показник тісноти зв'язку для випадку лінійної залежності буде

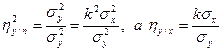(3.19)

Отримане відношення служить для визначення вимірника тісноти зв'язку між змінними в разі їх лінійної залежності, і має назву коефіцієнта кореляції r_y/х.

Якщо замість К підставити формулу для його обчислень 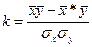, то матимемо

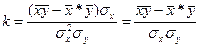. (3.20)

Коефіцієнт кореляції показує, на яку частину середнього квадратичного відхилення або σ_y змінюється функція у, якщо аргумент Х збільшується (зменшується) на своє середньоквадратичне відхилення σ_х. Знак коефіцієнта кореляції співпадає із знаком коефіцієнта регресії, а його чисельне значення коливається в межах

-1≤r_y/х≤1. (3.21)

Суттєвість коефіцієнта кореляції при заданому рівні значущості 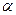=0,05 або 5% перевіряємо за умовою

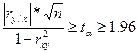, (3.22)

де t 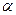визначається за умовою 2ф(t).

Приклад. Визначити гарантійну вірогідність істотності коефіцієнта кореляції r_y/х =-0,745 при n=52 спостережень.

Вирішення

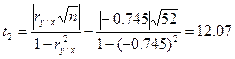. (3.23)

При 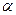=0,05 табличне значення t=1,96, що значно менше розрахункового. При t=12,07 довірчий інтервал в генеральній сукупності містить коефіцієнт кореляції з довірчою вірогідністю

P=2ф(12,07)=100%. (3.24)

Лінійність (нелінійність) зв'язку між змінними перевіряється шляхом:

- порівняння абсолютних значень (r_y/х)= η_y/х;

- статистично з використанням довірчого інтервалу. При цьому кореляційне емпіричне відношення η_y/х повинне покриватися довірчим інтервалів для (r_y/х):

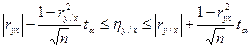(3.25)

з довірчою вірогідністю 2ф(t_α)=1-α.

Отже, якщо нерівність задовольняється при 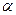=0,05, то приймаємо гіпотезу лінійності, якщо ж нерівність не задовольняється, то приймаємо гіпотезу нелінійної кореляційної залежності між у і х.

Завершальним дослідженням парного рівняння є перевірка відповідності виведеного рівняння описуваному реальному процесу. Якщо отримано декілька рівнянь регресії, то кращим слід читати те з них, яке ближче до закономірності по суті досліджуваного процесу, що вивчається. Слід оцінити ступінь близькості результатів розрахунків по кожному з отриманих рівнянь до звітних даних. Цей ступінь оцінюється по залишковій теоретичній дисперсії 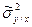, яка характеризує розкид досліджених точок кореляційного поля навколо теоретичної лінії регресії під впливом чинників, що не враховані в отриманому рівнянні.

Залишкова теоретична дисперсія визначається з рівняння

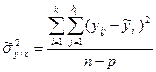, (3.26)

де n - обсяг вибірки;

Р - число параметрів рівняння;

К - число інтервалів;

h - число спостережень в i-му інтервалі;

y_ij - значення досліджених даних функціональної ознаки;

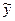- розрахункове значення функціональної ознаки, обчислене за рівнянням регресії.

Якщо складено декілька рівнянь регресії і для кожного обчислена залишкова дисперсія, то з декількох рівнянь регресії, рівноцінних по суті, перевагу слід віддати тому, в якого залишкова дисперсія менше.

Для управління регресії з одним аргументом Х залишкову дисперсію обчислюємо за формулою

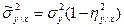. (3.27)

Одним з ознак згоди початкових даних з отриманим рівнянням служить нормальність розподілу відхилень досліджених даних від розрахункових (y_ij- 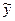_xi) зі середнім значенням, рівним нулю, і середнім квадратичним відхиленням, рівним σ_y/х. Чим ближче розподіл цих відхилень до вказаного нормального закону, тим краще узгоджуються вихідні дані з виведеним рівнянням регресії. Обчисливши всі відхилення (y_ij- 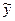_xi), перевіряємо наявність нормального закону їх розподілу візуально і за критерієм згоди.

Таким чином, дослідження управління в тій або іншій формі полягає у визначенні його параметрів (із вирішення системи нормальних рівнянь), підстановці в отримане рівняння всіх вихідних значень аргументу, розрахунку відповідних значень 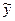_ij, порівнянні розрахункових значень 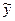_i із вихідними значеннями, обчисленні суми квадратів відхилень розрахункових значень від вихідних і визначення залишкової дисперсії 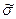^2y/х_. Найкраща форма визначається за найменшою залишковою дисперсією. За такою схемою визначаються форми зв'язку у по всіх аргументах.

Існує і критерій адекватності, запропонований Фішером, заснований на порівнянні залишкової теоретичної дисперсії 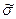²_y/х і загальної дисперсії σ_y². Розглядається відношення 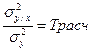і порівнюється з табличним (для 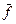% Фішера знайдено розподіл і складена спеціальна таблиця) при заданому рівні значущості і різних ступенях свободи.

Загальна дисперсія σ_y² досліджених даних від їх середнього значення встановлюється з урахуванням числа ступенів свободи :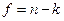

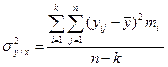, (3.28)

де К – число інтервалів у вибіркових даних.

Залишкова теоретична дисперсія 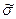^2y/х встановлюється як різниця розрахункових 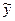_i і середніх інтервальних значень 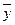_i з урахуванням числа ступенів свободи d₁=K-P і d₂=n-K,

де Р – число параметрів управління.

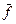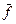Якщо _рас ≤ _табл, то при заданому рівні значущості складене рівняння регресії затверджується. Вірогідність помилки тим менше чим більше рівень значущості α%.

У разі, коли чисельник 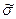^2y/х менше знаменника σ_y², то міняємо їх місцями разом з відповідними ступенями свободи d₁=K-P і d₂=n-K.

(3.52)

при 5% рівні значущості t=1,96.

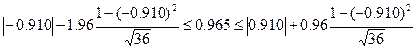. (3.53)

0,854 ≤ 0,965 ≤ 0,967 (3.54)

Теоретична лінія регресії представлена на рис.3.2.

Парні рівняння регресії 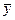_xj=d(xj) описують залежність функціональної ознаки від кожного окремо взятого чинника - аргументу без урахування його взаємозв'язку з іншими. Це може спотворювати дійсне положення, призводити до невиправданих висновків і пропозицій. Треба виявити відособлений "приватний вплив" кожного окремого чинника, які в досліджуваному процесі виступають у взаємозв'язку.

Проблема відшукання такого рівняння, яке показало б ізольований вплив на показник кожного окремого чинника, що вивчається, розв'язується за допомогою рівняння множинної регресії.

Ставиться завдання визначення такої функції F(X1,X2...X_p), яка математично описувала б зміну середнього значення ознаки у, що вивчається, залежно від аргументу Х1, Х2..Хр з урахуванням особливостей процесу і близьким охопленням вихідних даних:

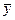_х1, _{х2, ....хр=F}(Х1, Х2...Хр). (3.55)

Поставлене завдання розв'язується на основі знання сутності процесу і попереднього виявлення одновимірної залежності

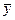_хj=dj (Xj), де j=1,2...P. (3.56)

При об'єднанні парних рівнянь в єдине множинне необхідно чітко розрізняти дві ситуації:

- при виборі рівнянь парної регресії 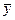_хj= d (Xj) (1) змінна у не піддавалася функціональним перетворенням;

- при виборі рівнянь парної регресії 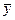_хj1= d (Xj) (2) величина у піддавалася функціональним перетворенням виду 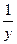, ℓ_g y, y² та ін.

У першій ситуації будь-яка парна залежність може бути з'єднана в множинне рівняння, яке можна отримати підсумовуванням виразів типу (1):

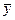_х1, _х2.._хр=F(X1, X2...Xp)= 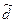₁(x1) + ₂(x2)+ 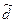_.+ p(_xp) (3),

де j=d(xj) – функція типу ij (xj) з невизначеними коефіцієнтами, обчисленими за способом найменших квадратів. Так, рівняння прямої 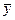=А₁Х1+В1 і гіперболи 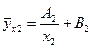об'єднуються в рівняння множинної регресії 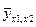в якому параметри а, b і с визначаються методом найменших квадратів з системи нормальних рівнянь:

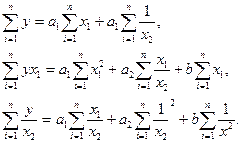(3.57)

У другій ситуації парні рівняння (1) об'єднуються в єдине множинне при будь-якому виді функції (2), але тільки у тому випадку, коли всі функціональні перетворення у однакові. У такій ситуації функціональні середні всіх парних рівнянь (2) співпадають і за допомогою загального множника перетворюють в шукану середню (звичайно в арифметичну середньою).

Як було рекомендовано вище, підбираємо функціональні перетворення змінних, рівняння виду (2) до лінійного виду, а значить шукане допоміжне множинне рівняння (3): перетвориться до вигляду

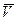_u1,_u2…._up=a₁ u₁+ a₂ u₂+….a_p u_p. (3.58)

Отже, оперуючи далі перетвореними змінними V і Uj, можна обмежитися методикою складання лінійного множинного рівняння, використовуючи всі переваги лінійної регресії:

- попереднє знаходження стандартизованого рівняння V по U1, U2... Up за допомогою кореляційної матриці;

- дослідження зворотної кореляційної матриці;

- дослідження суттєвості й незалежності коефіцієнтів регресії;

- аналіз бета – коефіцієнтів;

- аналіз зміни детермінації як показника тісноти зв'язку.

Якщо об'єднується парна лінійна залежність виду 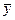=kx+b, то приходимо до вирішення задачі визначення множинної регресії вигляду

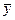_{х1, х2}… _хр =а₁ х₁ + а₂ х₂ +…+а_р х_р (3.59)

або інакше як і в разі, коли у функціонально не перетворювався, коефіцієнти а₁, а₂…а_р рівняння множинної регресії можуть бути визначені методом найменших квадратів:

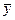_{х1, х2}… _хр- у=а₁ (х₁- 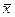₁) а₂ (х₂- 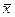₂)+……а_р(х_р- 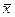_р). (3.60)

Проте при цьому буде утруднене зіставлення ступеня впливу окремих чинників-аргументів на функцію.

Більш зручно переходити до стандартизованого масштабу змінних, використовуючи формули

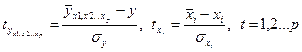, (3.61)

При цьому слід мати на увазі, що всі середні значення стандартизованих величин t_yx1, x₂…x_p т.е. 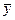і t_xi або x_i рівні нулю, а їх дисперсії σ_ij² и σ_txi² =1.

Разом з тим коефіцієнти кореляції між стандартизованими величинами зберігають колишні значення, тобто r_ty = r_yti, r_txi = r_xi. У результаті стандартизації рівняння множинної регресії набуває вигляду

t 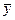_xi = β₁ t₁ + β₂ t₂ +… + β_p t_p, (3.62)

де, β₁, β₂…. β _р – невідомі коефіцієнти регресії в стандартизованому масштабі;

t_yx1, t₁, t₂….tp – стандартизовані значення змінних.

Для визначення β- коефіцієнтів виходимо з принципу найкращого наближення розрахункових значень до вихідних даних, що лежить в основі методу найменших квадратів. Відсівається таке лінійне рівняння, щодо якого сума квадратів відхилень заданих значень t_y, _1,2 …. _p від розрахункових по рівнянню якнайменша з усіх можливих для рівнянь такого виду.

Ця вимога приводить до системи лінійних рівнянь щодо шуканих β-коефіцієнтів і називається системою нормальних рівнянь:

r_y1 = β₁ + r₁₂ β₂ +……+ r_1p β_p

r_y2 = r_{2 1} β₁ + β₂+……+ r_2p β_p

............................................... . (3.63)

r_yp = r_p1 β₁ + r_p2 β₂ +…….+ β_p.

Як видно, для отримання багатофакторного рівняння, крім "зовнішніх парних коефіцієнтів" кореляції між у і х_i, тобто r_y1, r_y2 і т.д. вимагається знайти "внутрішні коефіцієнти" кореляції між чинниками-аргументами, тобто r₁₂, r₁₃…… r_1р.

Правило складання системи нормальних рівнянь для відшукання β- коефіцієнтів формулюється таким чином: за коефіцієнти при невідомих β₁, β₂….. β_р приймаються "внутрішні коефіцієнти" кореляції між чинниками-аргументами, а як вільні члени - "зовнішні коефіцієнти" кореляції між функцією і кожним з чинників.

Регресійну модель в більшості випадків розглядають як інструмент аналізу, планування і управління виробництвом. Звідси особливо строгі вимоги ставляться до надійності, адекватності й точності кожного коефіцієнта моделі. Якщо стандартна помилка знайденого коефіцієнта регресії перевершує його за абсолютною величиною, то не можна поручитися за достовірність не тільки того, на скільки одиниць свого найменування в середньому змінюється 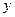при зміні Х на одиницю свого вимірювання, але і за напрям впливу даного чинника-аргументу.

Точність визначення коефіцієнтів множинної регресії суттєво залежить від ступеня стійкості системи нормальних рівнянь або, інакше, від ступеня обумовленості кореляційної матриці.

Система нормальних рівнянь є добре обумовленою, якщо малим змінам коефіцієнтів відповідають малі (того ж порядку) зміни рішень. Інакше кажучи, має місце безперервний зв'язок між коефіцієнтами системи рівнянь і її коренями - корені системи стійкі при малих змінах її коефіцієнтів.

Приклад. У табл. 3.5 наведена матриця коефіцієнтів кореляції собівартості перевезення пасажирів міським транспортом по трьох чинниках

Таблиця 3.5 – Матриця коефіцієнтів кореляції

При визначенні залежності собівартості перевезення пасажирів від Х₁ і Х₃, β-коефіцієнти знаходимо з вирішення системи нормальних рівнянь

β₁ - 0,7294 β₃ = -0,9108; (3.64)

-0,7294 β₁ + β₃ = 0,9055. (3.65)

Система має рішення

β₁ = -0,5348, β₃ = 0,5208. (3.66)

Якщо провести округлення всіх коефіцієнтів до десятих часток одиниці, отримаємо систему

β₁ – 0,7 β₃ = -0,9; (3.67)

-0,7 β₁ - β₃ = 0,9. (3.68)

Система має рішення

β₁ = -0,5294, β₃ = 0,5185. (3.69)

При цьому зміни коефіцієнтів:

∆а₁₃ = -0,7294-(-0,7)= -0,0294; (3.70)

∆b₁ = -0,9108-(-0,9)= -0,0108; (3.71)

∆b₃ = 0,9055-0,9 = 0,055. (3.72)

І відповідні зміни коренів:

∆ β₁ = -0,5348-(-0,5294)= -0,0054, (3.73)

∆ β₃ = 0,5208-0,5185= 0,0023 (3.74)

того ж порядку; корені системи стійкі.

Проте існують системи, погано обумовлені, в яких малим змінам коефіцієнтів відповідають значні зміни рішень.

Приклад. Розглянемо систему нормальних рівнянь для визначення β- коефіцієнтів двофакторної моделі залежності собівартості перевезення пасажирів від Х₁ і Х₂, β- коефіцієнти знаходимо з вирішення системи нормальних рівнянь:

β₁ – 0,8803 β₂ = -0,9108; (3.75)

-0,8803 β₁ + β₂ = 0,9012. (3.76)

Система має рішення

β₁ = -0,5219, β₂ = 0,4418. (3.77)

Якщо провести округлення всіх коефіцієнтів до десятих часток одиниці, отримаємо систему

β₁ – 0,9 β₂ = -0,9; (3.78)

-0,9 β₁ + β₂ = 0,9. (3.79)

Система має рішення:

β₁ = 0,4737, β₂ = 0,4736. (3.80)

При цьому зміни коефіцієнтів

∆а₁₂ = -0,8803-(-0,9)= -0,0119; (3.81)

∆b₁ = -0,9108-(-0,9)= -0,0108; (3.82)

∆b₂ = 0,9012-0,9= -0,001 (3.83)

і відповідні зміни коренів:

∆ β₁ = -0,5219-(-0,4737)= -0,048; (3.84)

∆ β₂ = 0,4418-0,4736= -0,0318 . (3.85)

Зміна другого кореня перевищує його значення. Змінився навіть знак кореня. Крім того, отримане рішення значно перевищує зміни коефіцієнтів системи. Отже регресійна модель, побудована за допомогою β-коефіцієнтів, знайдених по цій матриці, виявилася б нестійкою і економічні висновки з неї б були неточні й ненадійні. Стійкість системи нормальних рівнянь є необхідною умовою надійності економіко-математичної моделі.

Особливо часто явище нестійкої системи має місце в моделях з великим числом параметрів, де проблема обумовленості має найважливіше значення.

Виявивши нестійкість системи нормальних рівнянь, треба знайти причину цього явища і можливість його усунення.

Звичайно погано обумовлена система нормальних рівнянь має місце за наявності тісних кореляційних зв'язків між аргументами, що включаються в модель.

Лінійна залежність деяких аргументах в генеральній сукупності інших називається мультиколінеарністю.

Якщо в генеральній сукупності два аргументи, наприклад Х₁ и Х₂ лінійно залежать один від одного, то система з Р невідомими зводиться до системи Р-1 невідомими. Така система Р рівнянь є невизначеною, а її матриця виродженою. За допомогою такої системи β- коефіцієнти не можуть бути однозначно визначеними. Отже, багатофакторна модель , що включає обидва аргументи Х₁ и Х₂, не може бути складеною.

Система рівнянь може виявитися погано обумовленою і її рішення будуть нестійкі, якщо в стовпцях або в рядках матриці розташовуються пропорційні значення "внутрішніх коефіцієнтів" кореляції між коефіцієнтами.

Явище мультиколінеарністі, тобто лінійна залежність одного з аргументу від інших виявляється декількома способами:

- професійними міркуваннями по суті досліджуваного явища;

- інструкцією заснованої на складанні "внутрішніх і "зовнішніх" коефіцієнтів" кореляції кожного з аргументів. Якщо "внутрішній коефіцієнт" кореляції більше "зовнішнього", то даний аргумент в рівняння множинної кореляції не слід включати;

- використанням статистичного критерію мультиколінеарністі (Феррара і Гюбера). Для цього розглядається величина

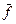_j = (C_ij-1) 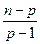, (3.86)

де Cij – діагональні елементи матриці, зворотної до кореляційної, знайденої за вибірковими даними;

n – обсяг вибірки;

p – число аргументів у рівнянні множинної регресії.

Зворотною по відношенню до даної називається матриця, яка, будучи помноженою як справа, так і зліва на дану матрицю, дає одиничну матрицю.

Для матриці А зворотна їй позначається через А^-1. Тоді за визначенням маємо:

А^-1*А = А* А^-1 = Е (3.87)

Якщо існує зворотна матриця А^-1, то матриця А називається зворотною. Для виродженої матриці зворотної матриці не існує, оскільки її визначник рівний нулю.

Визначник зворотної матриці рівний зворотній величині визначника даної матриці, що дає можливість обчислення зворотної матриці за допомогою визначників. Для цього використовуються поняття мінору і доповнення алгебри.

Мінором М_ij елемента а_ij визначника Д=(О_ij) називається такий новий визначник, який отриманий з даного визначника викреслюванням рядка і стовпця, що знаходиться через даний елемент матриці А.

Доповненням алгебри елемента а_ij визначника називається мінор М_ij цього елемента, взятий зі знаком (-1). Доповнення алгебри елемента а_ij позначається через А_ij. У прийнятому нами позначенні матимемо:

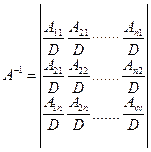(3.88)

Ферраром і Глобером доведено, що статична величина 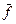_j підкоряється розподілу Фішера з (n-p) і (р-1) ступенями свободи. Отже, для виявлення мультиколінеарності використовується звичайний прийом перевірки статистичних гіпотез. Обчисливши вираз 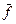_j (j=1,2…р), порівнюємо їх значення з табличними значенням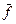и _5% и 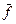_1% при відповідних ступенях свободи [ (n-p) (p-10) ].

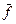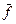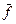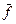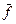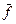Якщо _j < _5%, то гіпотеза відсутності мультиколінеарності j-го аргументу з іншими в генеральній сукупності стверджується. Навпаки, при _j > _5% - відкидається гіпотеза відсутності мультиколінеарності j-го аргументу з іншими в генеральній сукупності. При _5% < _j < 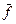_1% використовуються засоби послаблення мультиколінеарності шляхом переходу до нелінійних залежностей та ін.

Висновки про виключення якогось аргументу супроводяться логічним аналізом. По аргументах, що збереглися, повторюється перевірка мультиколінеарності.

Управління множинної регресії виявляється тим точніше і надійніше, чим слабше внутрішні кореляційні зв'язки між аргументами.

Знайдені в результаті рішення кореляційної матриці β- коефіцієнти показують на яку частину середньоквадратичного відхилення σу змінюється середнє значення функції, якщо відповідний аргумент зменшується або збільшується на юшок, а інші аргументи залишаються незмінними.

Найбільш доцільно відшукувати рівняння множинної регресії шляхом послідовного підключення до парного рівняння решти аргументів в порядку їх значущості (економічної, технологічної і т.п.). У цьому випадку виявляється можливість на кожному етапі аналізувати:

- обумовленість вирішуваної системи за чисельним значенням її визначника (детермінатора);

- зміна β- коефіцієнтів, чисельне значення яких має бути менше 1, а знак не суперечити логіці;

- зростання коефіцієнта множинної кореляції R і убування залишкової дисперсії .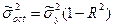

Методика послідовного підключення аргументів складається з наступних операцій.

1.Обирається аргумент Х₁, якому відповідає найбільший за абсолютним значенням "зовнішній коефіцієнт" кореляції

| r _y1| = max | r _yi|, j = 1,2….q. (3.89)

За аргументом Х₁ записується рівняння

t_y1 = t_y1 t_x1. (3.90)

2. Приєднується аргумент Х_io, для якого

| r _xj X₁ | = min | r _{xj x1} |, j = 2,3,… q. (3.91)

Складається система нормальних рівнянь

r _yх1 = β₁ + r _хjo β₂; (3.92)

r _{y xjo} = β₁ r _{хjo x1} + β₂ (3.93)

і обчислюються значення β₁ и β₂. Визначаються

R²_{y, x1 хjo} = β₁ r_yx1 + β₂ r _{y xjo}; (3.94)

σу, _{х1 xjo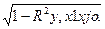} = (3.95)

Порівнюється R²_{y, x1 хjo}, σу, _{х1 xjo} відповідно з r ²_yx1, σу _х1.

Переконуються в справедливості нерівності

R²_{y, x1 хjo} ≥ r ²_yx1 ; σу, _xjo ≤ σу _х1. (3.96)

У противному разі замінюється чинник аргумент іншим X_j1, а аргумент X_j0 переноситься на останнє місце.

3. Далі приєднується наступний аргумент X_j1 і розв'язується система з трьома невідомими:

r _{y х1} = β₁ + β₂ r_{х1 xjo} + β₃ r_{х1 xj1}; (3.97)

r _{y xjo} = β₁ r_{х1 xjo} + β₂ + β₃ r _{xjo xj1}; (3.98)

r _{y xj1} = β₁ r_{х1 xjo} + β₂ r _{xjo xj1} + β₃. (3.99)

Обчислюються значення β_1, β₂ и β₃. Визначаються

R²_{y, x1 хjo xj1} = β₁ r _{y х1} + β₂ r _{y xjo} + β₃ r _{y xj1}; (3.100)

σу, _{xjo xj1} = σу 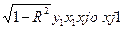(3.101)

і порівнюються з R²_{y, x1 хjo} і σу, _{x1 хjo}. Переконуються в справедливості нерівності

R²_{y, x1 хjo xj1} ≥ R²_{y, x1 хjo}; (3.102)

σу, _{x1 хjo xj1} ≤ σу, _{x1 хjo}. (3.103)

У противному разі поступають аналогічно П.2.

Дослідження ведуть до тих пір, поки не будуть апробовані чинники-аргументи і збережені тільки ті з них, для яких β_j–коефіцієнти суттєві й лінійно незалежні. У результаті виходить множинне рівняння в стандартизованому масштабі.

Від рівняння множинної регресії в стандартизованому масштабі

t 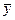_xi = β₁ t₁ + β₂ t₂ + ….+ β_p t_n (3.104)

до рівняння множинної регресії в натуральному масштабі

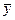_{х1, х2…Хр} = а₁х₁ + а₂х₂ + ….+ а_рх_р +b. (3.105)

Перехід здійснюється подвійно.

1. Шляхом використання формул

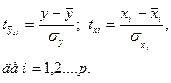(3.106)

При цьому маємо

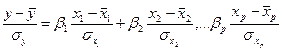(3.107)

Підставивши відомі значення 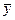, σxi, σу, β_i і 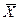_I, отримаємо рівняння множинної регресії в натуральному масштабі, в якому чисельне значення вільного члена додатково визначати не потрібно.

2. Невідомі коефіцієнти а_i в рівнянні множинної регресії в натуральному масштабі визначають з виразу

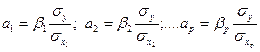. (3.108)

Чисельне значення вільного члена

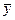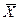b = -(а_{1 1}+ а_{2 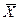2} + …+ а_{р 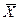р}). (3.109)

Для з'ясування математико-статистичного змісту множинної кореляції всю досліджувану групу змінних слід розглядати як один чинник-аргумент. Чисельне значення коефіцієнта множинної кореляції визначають за формулою

R= 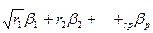. (3.110)

При цьому 0≤ R≤1. Коефіцієнт надійності

М = 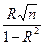. (3.111)

Стандартну помилку (середню квадратичну похибку) коефіцієнта множинної кореляції визначають за формулою

σ_R = (1-R)/ 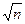, (3.112)

де n-обсяг вибірки.

Сукупний вплив врахованих змінних на функцію визначається коефіцієнтом загальної детермінації R², а окремих чинників-аргументів за чисельними значеннями приватної детермінації r_iβ_i:

R² = r₁β₁ + r₂β₂+…..+ r_pβ_p. (3.113)

Стандартну (систематичну) похибку 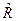² обчислюють за формулою

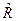² = 1-(1- R²) 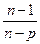, (3.114)

де Р - число параметрів рівняння регресії. З рівняння множинної регресії можна отримати рівняння чистої (приватної) регресії 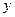по кожному з аргументу X_i. Для цього фіксується значення всіх аргументів, окрім X_i, на середньому рівні.

Отримане рівняння описує, як в середньому змінюється із зміною X_i, якщо всі інші аргументи постійні й закріплені саме на своїх середніх рівнях.

Приклад. Відповідно до наведеною методики скласти рівняння множинної регресії собівартості перевезення пасажирів 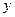від чинників: X₁ – середньодобове перебування рухомого складу на лінії; X₂ – середньодобова кількість пасажирів, що перевозяться, тис. чол.; X₃ – пробіг рухомого складу на 1000 пасажирів, км, що перевозяться. Відомо, що 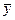= 78,9 коп., σу =3,5104, а в таблиці матриці наведені внутрішні й зовнішні коефіцієнти кореляції.

Таблиця 3.6 - Внутрішні й зовнішні коефіцієнти кореляції

	Х1 = t	X2 = 1/A	X3 = П	ryx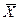i	i	σxi
t 1/A П	-0,8803 -0,7294	-0,8803 0,9376	-0,7294 0,9376	-0,9108 0,9012 0,9055	11,757 0,0187 167,14	0,1611 0,00122 7,3996

Етап 1.Послідовно підключаються чинники-аргументи, в першу чергу з найбільшим "зовнішнім коефіцієнтом" кореляції і найменшим "внутрішнім". У нашому прикладі найбільше "зовнішні коефіцієнти" кореляції з 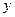мають Х₁ и Х₃.

Система нормальних рівнянь має вигляд

β₁ – 0,7294 β₃ = -0,9108; (3.115)

-0,7294 β₁ + β₃ = 0,9055. (3.116)

Отримане рішення

β₁ = -0,5348 и β₃ = 0,515. (3.117)

Визначаємо R²_{у, Х1 Х3} и σу,_Х1Х3

R²_{у, Х1 Х3} = -0,9108 (-0,5348) + 0,9055 * 0,515 = 0,9534; (3.118)

σу,_Х1Х3 = 3,51104 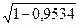= 0,7578. (3.119)

Порівнюємо R²_{у, Х1 Х3} і σу,_Х1Х3 з r²_yx, и σу,_Х1, де справедливі рівняння 0,9534 >0,9108, 0,7578 < 3,5104.

Складаємо рівняння множинної регресії по двох чинниках-аргументах:

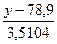= -0,5348 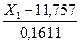+ 0,515 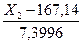(3.120)

Після відповідних перетворень виходить рівняння множинної регресії собівартості по двох чинниках–аргументах, середньодобовому перебуванні рухомого складу на лінії і пробігу рухомого складу на 1000 перевезених пасажирів

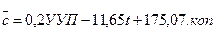. (3.121)

Етап 2. Приєднуємо наступний аргумент А- середньодобова кількість пасажирів, чол, що перевозяться. Складаємо систему нормальних рівнянь

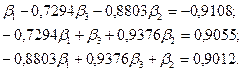(3.122)

Обчислюємо .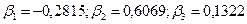

Рівняння множинної регресії по трьох чинниках–аргументах має вигляд:

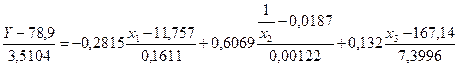. (3.123)

Після відповідних перетворень виходить управління множинної регресії пасажироперевезень по трьох чинниках – аргументах:

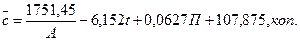(3.124)

Сукупний вплив облікових чинників на собівартість пасажироперевезень визначається загальною детермінацією, а окремих чинників аргументів за чисельними значеннями часткової детермінації 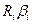, які складають:

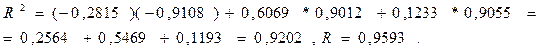
Отримані результати свідчать, що три чинники – аргументи, включені в множинну кореляційну залежність, на 92% обумовлюють собівартість пасажироперевезень міським електричним транспортом, у тому числі: середньодобове перебування рухомого складу на лінії - на 25,64%; середньодобова кількість пасажирів, що перевозяться - на 54,69%; пробіг рухомого складу на 1000 пасажирів, що перевозяться - на 11,93% при досить високому коефіцієнті кореляції R=0,9593.