Авторегресійні моделі прогнозування
Методика прогнозування цінна в тому випадку, якщо вона спирається на обґрунтовану теорію, що встановлює правомочність прогнозування за допомогою даної моделі і помилки вірогідності прогнозу. Оцінка такої помилки за допомогою функції зростання неможлива, тому особливий інтерес представляють авторегресійні моделі.
Авторегресією називається рівняння, що визначає змінну Хj у момент t (або t-й період) через її значення в попередні періоди: (t-1) (t-2)... (t-к). Лінійне авторегресійне рівняння записуємо у вигляді
Хt = а1 Хt-1 + а2 Хt-2 + + ак Хt-к. (4.18)
Першим етапом дослідження тимчасового ряду змінної Х є виділення загальної тенденції у вигляді функції d(t) і визначення залишків εt у формі εt = Хt - d(t) чи εt = d(хt).
Якщо залишки εt незалежні, тобто не можуть бути представлені як функція часу, то функція d(t) охоплює повністю еволюційну складову змінної Хt. При цьому залишається знайти закон їх розподілу εt і, прийнявши гіпотезу про збереження цього закону розподілу на прогнозований період, побудувати довірчий інтервал для прогнозованої величини Хt за функцією d(t). Якщо ж залишки εt залежні, тобто містять деяку тенденцію, то її можна виявити за допомогою коефіцієнта автокореляції. Проводячи зсув значень εt на один рядок і останнє значення переміщаємо на перше місце, одержуємо табл. 4.6.
Таблиця 4.6 – Залишки змінних ряду динаміки
| εt | εt-1 |
| ε1 | εn |
| ε2 | ε1 |
| ε3 | ε2 |
| ………… | ………….. |
| εn | εn-1 |
Обчислюємо циклічний коефіцієнт кореляції між рядами εt і εt-1 за формулою
r(εt, εt-1) = 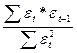 . (4.19)
. (4.19)
Ця формула (4.19) виходить із звичайної формули для визначення коефіцієнта кореляції, якщо покласти
∑ εt = ∑ εt-1 = 0; (4.20)
∑ (εt -1)2 = ∑ (εt)2 . (4.21)
Формула (4.20) виходить з того, що параметри функції d(t) визначаються за методом якнайменших квадратів, а формула (4.21) - з циклічної табл. 4.6.
Аналогічно, зсовуючи εt на 2,3….К рядків, одержуємо циклічну таблицю послідовних відхилень
Таблиця 4.7 - Циклічна таблиця послідовних відхилень
| t | εt | εt-1 | εt-2 | ……… | εt-к+1 | εt-к |
| ε1 | εn | εn-1 | εn-k+2 | εn-k+1 | ||
| ε2 | ε1 | εn | εn-k+3 | εn-k+2 | ||
| ε3 | ε2 | ε1 | εn-k+4 | εn-k+3 | ||
| …. | …. | …. | …. | …. | …. | |
| К | εk | εk-1 | εk-2 | ε1 | εn | |
| К+1 | εk+1 | εk | εk-1 | ε2 | ε1 | |
| К+2 | εk+2 | εk+1 | εk | ε3 | ε2 | |
| ….. | ….. | …. | …. | …. | …. | …. |
| n | εn | εn-1 | εn-2 | εn-k+1 | εn-k |
За даними табл. 4.7 визначаємо всі циклічні коефіцієнти автокореляції:
r(εxt εxt-j) = 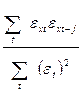 , i, j = 1,2,…..K; (4.22)
, i, j = 1,2,…..K; (4.22)
r(εxt-1 εxt-j) = 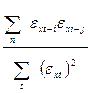 . (4.23)
. (4.23)
Циклічний коефіцієнт автокореляції не підпорядковується нормальному закону розподілу, його розподіл асиметричний, суттєві величини коефіцієнтів автокореляції при певному рівні значущості різні для позитивних і негативних його значень. 5% - й і 1% - й рівні значущості коефіцієнтів автокореляції подані в спеціальних таблицях. Знайдені значення r1, r2… rn-к-1 перевіряємо по таблиці 5% - х і 1% - х рівнів вірогідності коефіцієнтів автокореляції. Якщо | rстат. (n) | < | r5%. (n) |, то приймаємо гіпотезу неавтокорельованості залишків εt; якщо | rстат. (n) | > | r1%. (n) | відкидаємо гіпотезу їх неавтокорельованості.
За циклічними коефіцієнтами автокореляції складаємо матрицю і її обертаємо. Як і в разі звичайної регресії багаточинника, перевіряємо наявність мультиколінеарності кожного з чинників εxt-j, j=1,2-k від сукупності інших і зберігаємо тільки лінійно незалежні аргументи.
Будуємо лінійну авторегресійну модель
εt = а1 εt-1 + а1 εt-2 + ….+ ак εt-к, (4.24)
що виражає εt в період t за допомогою значень εt-j, j = 1,2…К за К попередніх періодів. При цьому в рівнянні повинні бути збережені тільки суттєві і лінійно незалежні коефіцієнти.
Якщо виявляються аj – коефіцієнти, що не задовольняють вказаним вимогам, то модель потребує перерахунку (починаючи з розрахунку автокореляційної матриці більш низького порядку).
Оскільки параметри рівняння тренда визначали за методом найменших квадратів, то в разі його коректного підбору відповідні відхилення підкоряються нормальному розподілу, і, отже, рівняння регресії можна відшукувати в лінійній формі
ℓn Xt = a1 ℓn Xt-1 + a2 ℓn Xt-2 +…….+ak ℓn Xt-k + F(t); (4.25)
Xt = a1 Xt-1 + a2 ℓn Xt-2 +……..+ an Xt-k + F(t). (4.26)
Яким повинне бути число членів рівняння, це питання слід вирішувати в поєднанні професійних вимог процесу, що по суті вивчається, з математико-статистичними критеріями. Так, якщо статистичний ряд містить тижневі дані, то особливий інтерес являє чотиричленна модель залежності рівня показника від тижневих рівнів за весь попередній місяць. У разі місячних даних цікава тричленна авторегресія, а для даних, зібраних по роках, – п’ятичленна.
Статистичні критерії покликані встановити відсутність автокорельованості залишків від віднімання з табличних значень εt їх розрахункових значень
ηt = εt – (a1 εt-1 + a2 εt-2 +…+ ak εt-2k). (4.27)
Існує декілька статистичних критеріїв. Один з них заснований на порівнянні середнього квадрата послідовних різниць ηt:
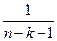
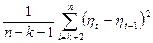 . (4.28)
. (4.28)
З дисперсією величини
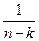
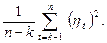 (4.29)
(4.29)
Складаємо відношення середнього квадрата послідовних різниць, до середнього квадрата самих величин:
К = 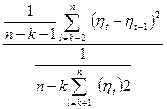 . (4.30)
. (4.30)
Якщо Кстат., потрапляє в допустиму область при рівні значущості 5%, а саме К5% (n-k) < Кстат (n-k) < К15% (n-k), то приймаємо гіпотезу неавтокорельованості залишків ηt, а, отже, і достатності числа членів К авторегресійної моделі.
Якщо ж Кстат (n-k) < К% (n-k) або Кстат > К1% (n-k), то відкидаємо гіпотезу неавтокорельованості залишків ηt і рахуємо число членів рівняння недостатності. У цьому випадку число членів рівняння треба збільшити, якщо довжина ряду дозволяє це.
Користуючись для прогнозу розробленими рівняннями, можна знайти довірчий інтервал для значення прогнозованого показника.
Якщо прогнозований показник рівний 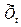 , то розмір показника Хt записуємо у вигляді
, то розмір показника Хt записуємо у вигляді
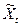 -
- 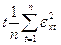 ≤ Xt ≤ +
≤ Xt ≤ + 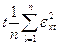 . (4.31)
. (4.31)
Викладена методика складання авторегресійних моделей, використані критерії і побудований довірчий інтервал можна застосовувати тільки для великих вибірок, коли довжина ряду n не менше 30.
Помилка прогнозу по отриманих рівняннях визначається за дисперсії εt. Оскільки
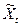 - Хt = εt, (4.32)
- Хt = εt, (4.32)
то Βер 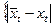 = | εt| ≤ tα σε
= | εt| ≤ tα σε 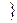 = Pα, (4.33)
= Pα, (4.33)
де Pα – задана вірогідність, Pα = 1-α, а tα - відповідна межа по С (n-k) ступеням свободи Стьюдента:
σε =  . (4.34)
. (4.34)
Розглянемо приклади складання авторегресійних моделей.
Одночленна модель. Щомісячний пробіг рухомого складу міського електротранспорту на 1000 пасажирів, що перевозяться, заданий рядом в графі 2 табл. 4.8. Наявність експоненціального ряду (див. рис. 4.3.) дозволяє розраховувати на придатність одночленної моделі 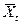 = а1Хt-1.
= а1Хt-1.
Система нормальних рівнянь для визначення параметра а1 має вигляд
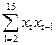 = а1
= а1 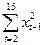 . (4.35)
. (4.35)
З табл. 4.3. (графи 4 і 5) виходить 367673,4 = 364278,2 а1
Звідки а1 = 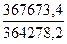 = 1,0087 ≈ 1,01.
= 1,0087 ≈ 1,01.
Одержуємо рівняння 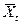 = 1,01 Хt-1. Обчислюємо значення
= 1,01 Хt-1. Обчислюємо значення 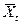 = 1,01 Хt-1 (графа 6) і знаходимо значення εt = Xt -Хt-1 (графа 7) ∑ εt = 9,4, що несуттєво в порівнянні з розмірами Xt.
= 1,01 Хt-1 (графа 6) і знаходимо значення εt = Xt -Хt-1 (графа 7) ∑ εt = 9,4, що несуттєво в порівнянні з розмірами Xt.
Обчислюємо коефіцієнт циклічної автокореляції r1. За графами 9 і 10 отримаємо
r1 = r(εt, εt-1) = 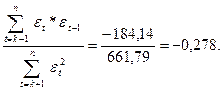 (4.36)
(4.36)
З табл. 4.3 знаходимо n1 = 15-1=14, r<0, r5% = -0,479.
Оскільки | r1| < | r5%|, кореляція εt, εt-1 несуттєва.
Аналогічно за графами 12 і 10 (табл. 4.8.) одержуємо r2 = 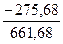 = 0,416, що свідчить про несуттєвість кореляції εt и εt-2.
= 0,416, що свідчить про несуттєвість кореляції εt и εt-2.
У даному випадку переважний критерій Дж. Неймана. Обчислюємо різницю εt -εt-1 за графами 13 і (εt -εt-1)2 – за графами 14. Одержуємо
K= 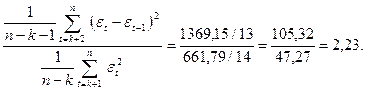 (4.37)
(4.37)
За табл. 4.3 для n1 = 14 рівень значущості К5% рівний 1,2725 при r > 0 і 3,0352 у разі r < 0. Розрахунки свідчать, що коли в генеральній сукупності автокореляція між залишками εt відсутня, то в 95% вибірок буде К > 1,272 у випадку r > 0 и К < 3,0352 при <.
У даному прикладі значення К потрапляє в допустиму область при 5% рівні значущості К > 1,2725. Отже, гіпотеза неавтокорельованості залишків εt стверджується і авторегресійне рівняння Xt = 1,01 Xt-1 приймається.
Помилка прогнозу при середньоквадратичному відхиленні
σε = 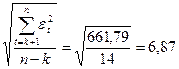 . (4.38)
. (4.38)
Складаємо
Вср =  ≤ tα *
≤ tα * 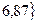 = Pa. (4.39)
= Pa. (4.39)
При 95%-й гарантійної вірогідності tα = 2,1 за табл. П.4[12] і помилка прогнозу не перевищить 14,42, що складає приблизно 8%:
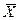 - 14,42 ≤ 1,01 Xt-1 ≤
- 14,42 ≤ 1,01 Xt-1 ≤ 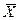 + 14,42 (4.40)
+ 14,42 (4.40)
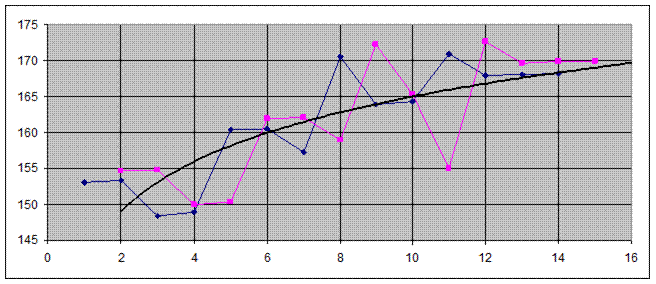
Рис. 4.3 - Одночленна авторегресійна модель:
1-вихідні дані; 2-одночленна авторегресія; 3-вирівнююча гіпербола.
Багаточленна модель. Щомісячна реалізація цегли (в тисячах штук) базою торгово – будівельних матеріалів за 20 місяців представлена в табл. 4.9 (графа 2). Треба скласти модель для прогнозування місячної потреби в цеглі на найближчі місяці.
Дата добавления: 2015-08-26; просмотров: 2375;
