Обобщенный закон Гука

Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного и как частый случай плоского напряженных состояний. Он может быть получен на основании закона Гука для линейного напряженного состояния и принципа независимости действия сил.

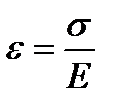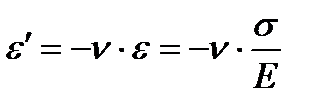Пусть задано произвольное объемное напряженное состояние с главными напряжениями s₁, s₂ и s₃. Представим его в виде суммы трех линейных напряженных состояний. Учитывая, что при линейном напряженном состоянии и запишем выражение для линейной относительной деформации в направлении :

.

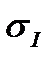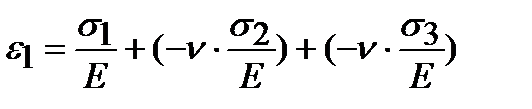Деформации в направлении действия главных напряжений равны

; ; .

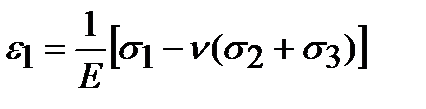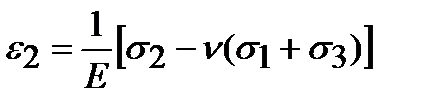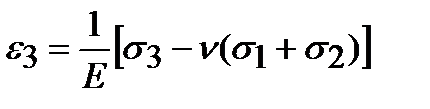Эти выражения носят название обобщенного закона Гука, записанного для главных площадок e₁, e₂, e₃ в направлении главных напряжений называются главными деформациями.

Соотношения обобщенного закона Гука могут быть записаны для любых (не главных) площадок, но так как при этом будут действовать кроме нормальных и касательные напряжения (рис. 3.10), необходимо добавить три соотношения для вычисления угловых деформаций. Таким образом, для произвольных площадок обобщенный закон Гука содержит шесть соотношений, связывающих деформации и напряжения:

_{; ;}

_{; ;}

_{; .}

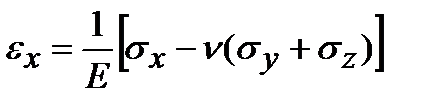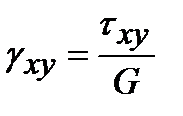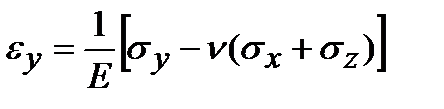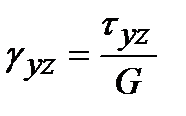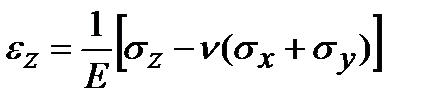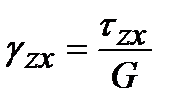Как известно, при деформации происходит изменение формы и объема тела. Рассмотрим относительное изменение объема тела при деформировании. Обратимся к рис. 3.1. Объем элементарного прямоугольного параллелепипеда до деформации 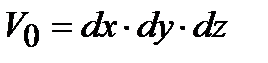. При деформировании длина каждого ребра может измениться на некоторую величину D и объем того же параллелепипеда после деформирования будет .

Тогда относительное изменение объема может быть вычислено следующим образом:

₌ .

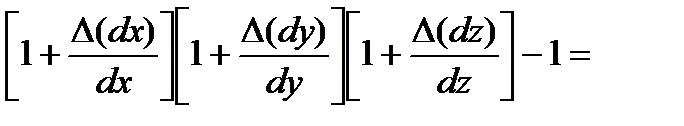
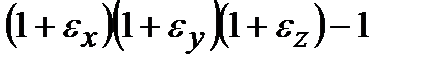Раскрывая скобки и пренебрегая слагаемыми более высокого порядка малости по сравнению с e, получим .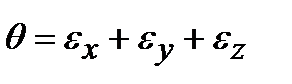

Подставляя e из обобщенного закона Гука, получим

.

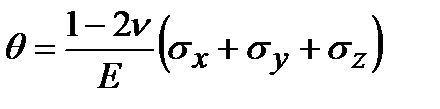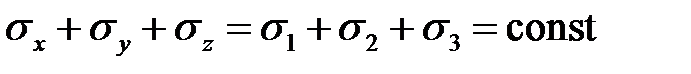Учитывая, что , запишем выражение для q в виде

.

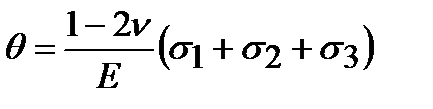Из формулы видно, что при положительных направлениях главных напряжений относительное изменение объема может быть положительной величиной, если только коэффициент Пуассона будет ν < 0,5. Таким образом, получается, что для всех существующих в природе материалов коэффициент Пуассона изменяется в пределах 0 £ n£ 0,5 и для большинства конструкционных материалов он равен ν = 0,2…0,3.

Также можно отметить, что если коэффициент Пуассона равен n = 0,5, то относительное изменение объема равно нулю. Резина имеет n ≈ 0,5 , следовательно, при приложении нагрузки её объём практически не меняется, она ведет себя как несжимаемая жидкость. Это свойство резины часто используется в экспериментальной практике.

Определим также относительное изменение объема при чистом сдвиге.

Так как при чистом сдвиге 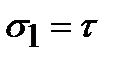, , 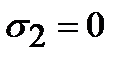, 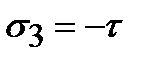то

.

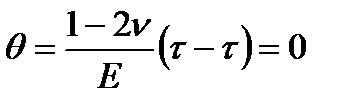Таким образом, относительное изменение объема при чистом сдвиге равно нулю.

Рассмотрим изменение удельной потенциальной энергии деформации в теле.

Удельной потенциальной энергией деформации u называется величина потенциальной энергии деформации U, накопленной в единице объема тела V. Для линейного напряженного состояния:

.

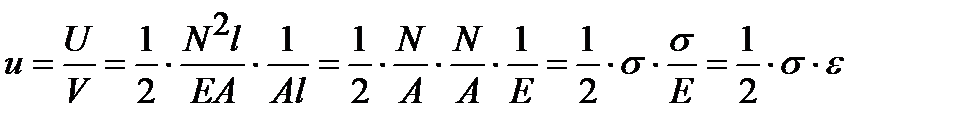Используя принцип независимости действия сил, полученный результат можно обобщить на случай объемного напряженного состояния:

.

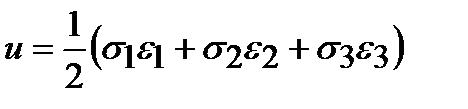В случае площадок общего положения (не главных площадок) выражение для удельной потенциальной энергии приобретает вид:

.

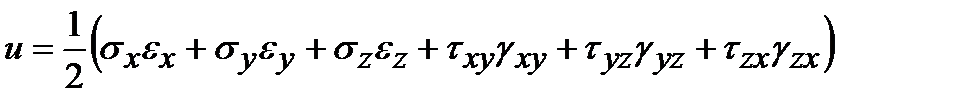Предыдущее выражение можно преобразовать с помощью формул обобщенного закона Гука к виду:

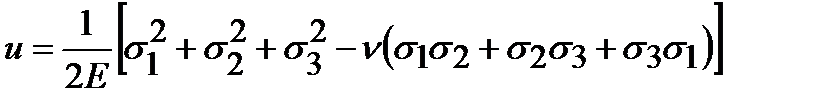. (3.5)

Рассмотрим напряженное состояние чистого сдвига. Запишем выражение удельной потенциальной энергии деформации по площадкам чистого сдвига:

.

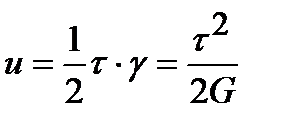С другой стороны, чистый сдвиг – это двухосное напряженное состояние с главными напряжениями 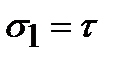; 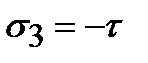, поэтому можно записать u как

.

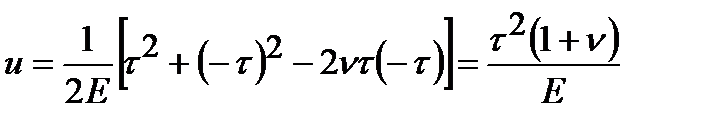Очевидно, величина удельной потенциальной энергии деформации u не должна зависеть от того, по каким площадкам она записана, поэтому

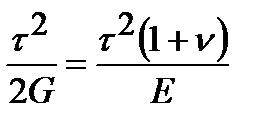, откуда, как упоминалось ранее .

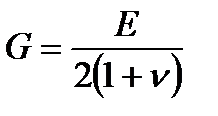Таким образом, постоянные упругости материалов, характеризующие жесткость при растяжении и сдвиге и поперечную деформацию, являются зависимыми. Поэтому достаточно определить лабораторным путем при растяжении две характеристики упругости Е и n, а третья G может быть вычислена аналитически.