Плоское напряженное состояние
Плоским, или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю (рис. 3.8).
Рассмотрим задачу определения напряжений в площадке общего положения (прямая задача).
Определим напряжения sx и txy, действующие по любой наклонной площадке a по известным главным напряжениям s1и s2 , т.е. решим так называемую прямую задачу теории напряженного состояния.
Для решения этой задачи воспользуемся принципом независимости действия сил. Представим плоское напряженное состояние в виде суммы двух независимых линейных напряженных состояний: первое – при действии только напряжений s1, второе – при действии только напряжений s2(рис. 3.9).
От каждого из напряжений s1, s2 напряжения sx1, sx2 и txy1,txy2 в произвольной площадке равны
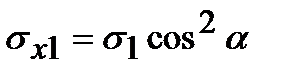 ;
; 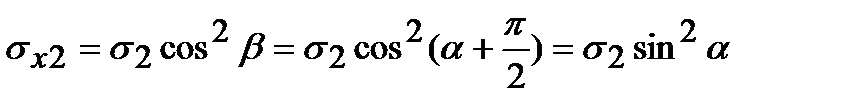 ;
;
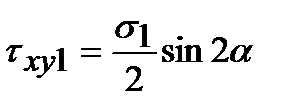 ;
; 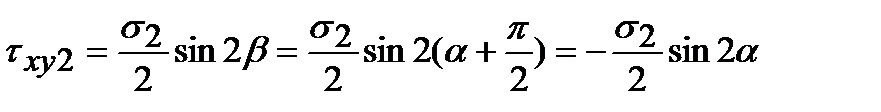 .
.
Таким образом, суммируя напряжения, возникшие при каждом линейном напряженном состоянии, получим
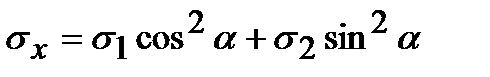 (3.1)
(3.1)
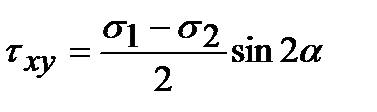 .
.
Если рассмотреть площадку с углом наклона 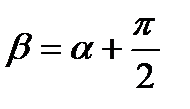 , перпендикулярную к площадке a, то можно доказать, как и для линейного напряженного состояния, что
, перпендикулярную к площадке a, то можно доказать, как и для линейного напряженного состояния, что
 ; (3.2)
; (3.2)
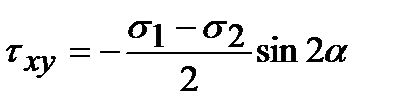 .
.
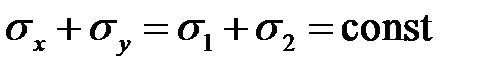 Суммируя нормальные напряжения, действующие по взаимно перпендикулярным произвольным площадкам, получим .
Суммируя нормальные напряжения, действующие по взаимно перпендикулярным произвольным площадкам, получим .
Сравнивая величины касательных напряжений, получим 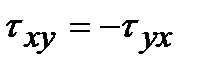 .
.
Наибольшие касательные напряжения действуют по площадкам, наклоненным к главным под углом a = 45о
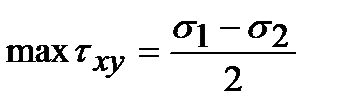 .
.
Дата добавления: 2015-08-21; просмотров: 860;
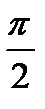
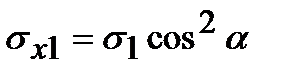 ;
; 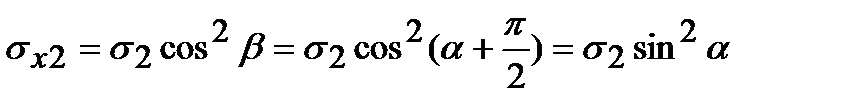 ;
;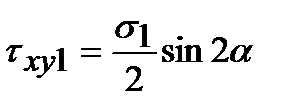 ;
; 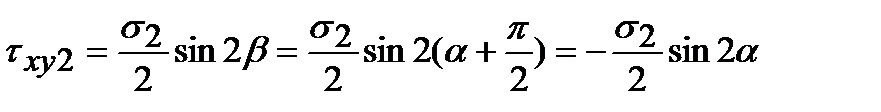 .
.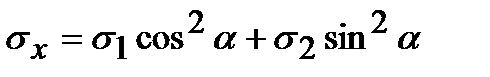 (3.1)
(3.1)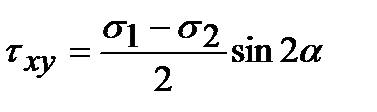 .
.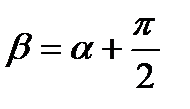 , перпендикулярную к площадке a, то можно доказать, как и для линейного напряженного состояния, что
, перпендикулярную к площадке a, то можно доказать, как и для линейного напряженного состояния, что ; (3.2)
; (3.2)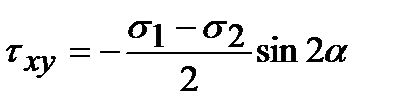 .
. 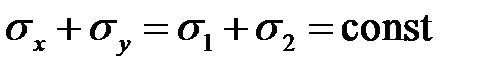 Суммируя нормальные напряжения, действующие по взаимно перпендикулярным произвольным площадкам, получим .
Суммируя нормальные напряжения, действующие по взаимно перпендикулярным произвольным площадкам, получим .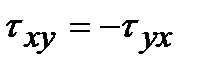 .
.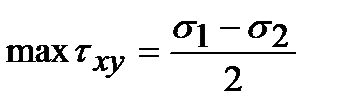 .
.