Рассмотрим частные случаи плоского напряженного состояния.
Всестороннее растяжение. Напряженное состояние, при котором главные напряжения, действующие по граням параллелепипеда, равны между собой s1 = s2 = s называется всесторонним растяжением. В этом случае получим
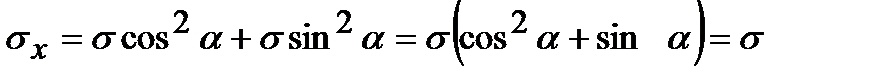 ,
,
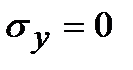 ,
,
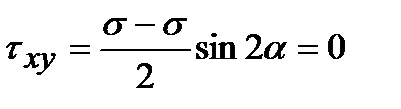 ,
, 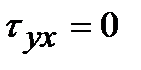 ,
,
т.е. нормальные напряжения в любой произвольной площадке равны между собой s1 = s2 = sх = sу = s, а касательные напряжения равны нулю: 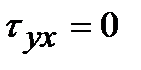 ,
, 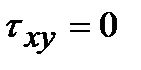 .
.
Чистый сдвиг. Пусть по граням параллелепипеда действуют главные напряжения 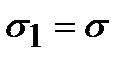 ,
, 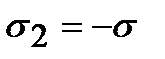 (рис. 3.10). Определим величины нормальных и касательных напряжений, действующих в площадках, повернутых под углом 45о к главным. Из формул (3.1) получим, что
(рис. 3.10). Определим величины нормальных и касательных напряжений, действующих в площадках, повернутых под углом 45о к главным. Из формул (3.1) получим, что
 ,
, 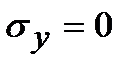 ,
,
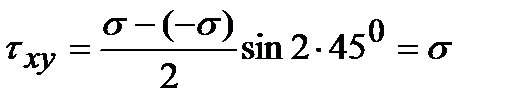 ,
, 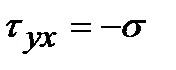 .
.
Напряженное состояние, при котором по граням выделенного элемента действуют только касательные напряжения, называется чистым сдвигом, а площадки – площадками чистого сдвига.
Экспериментально установлено, что существует линейная зависимость между углом сдвига g и касательными напряжениями t (рис. 3.11), являющаяся законом Гука при сдвиге 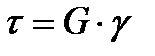 , где G – модуль сдвига, характеризующий способность материала сопротивляться сдвиговой деформации, т.е. характеризующая жесткость материала при сдвиге.
, где G – модуль сдвига, характеризующий способность материала сопротивляться сдвиговой деформации, т.е. характеризующая жесткость материала при сдвиге.
| s2= s |
| s |
| s |
| s1=s |
| tyx=-s |
| tyx |
| txy= s |
| txy |
| Рис. 3.10 |
| txy |
| txy |
| tyx |
| tyx |
| g |
| Рис. 3.11 |
Величина модуля сдвига связана с модулем упругости при растяжении Е и коэффициентом Пуассона ν соотношением
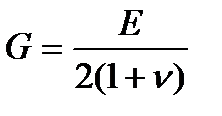 .
.
Рассмотрим задачу определения главных напряжений s1 и s2, а также положения главных площадок (угол a0) по известным напряжениям sх, sу, tху, действующим по двум взаимно перпендикулярным площадкам (обратная задача).
Пусть для определенности положим sх > sу. Из формул (3.1) и (3.2), можно получить
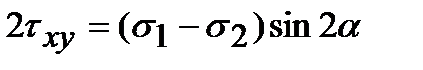 ,
,
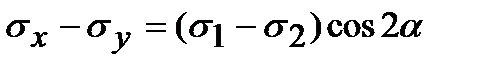 . (3.3)
. (3.3)
Исключив из этих формул s1 и s2, получим формулу для определения угла наклона главных площадок относительно заданной площадки. Обозначим этот угол a0. Так как направление отсчета углов a для площадки произвольного положения и угла a0 противоположны, то в полученной формуле необходимо изменить знак. Положительный угол a0 будем откладывать от направления внешней нормали к площадке, по которой действуют большие нормальные напряжения sх против хода часовой стрелки:
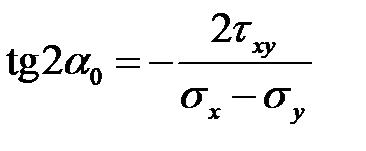
.
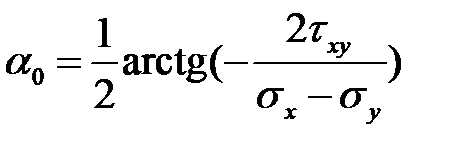 .
.
Откуда .
Для определения 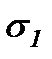 и
и 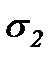 возведем каждое из соотношений (3.3) в квадрат и сложим их:
возведем каждое из соотношений (3.3) в квадрат и сложим их:
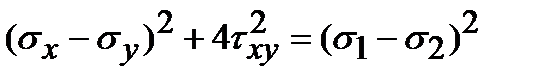 ,
,
тогда
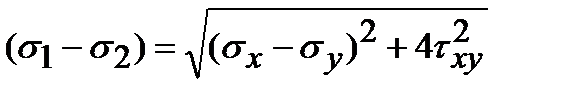 ,
,
а так как 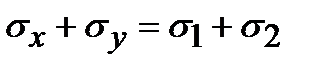 , то из двух последних соотношений получим:
, то из двух последних соотношений получим:
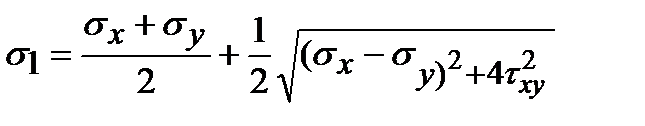 ;
;
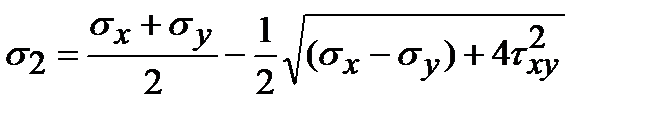 . (3.4)
. (3.4)
Большее главное напряжение s1 действует на площадке с углом наклона a0, вторая же главная площадка с напряжением s2 ей перпендикулярна, и ее нормаль наклонена под углом  к направлению sх. Положение главных площадок и направления главных напряжений представлены на рис. 3.12.
к направлению sх. Положение главных площадок и направления главных напряжений представлены на рис. 3.12.
| a0 |
| sx |
| s1 |
| txy |
| sy |
| tyx |
| s2 |
| sx |
| txy |
| tyx |
| sy |
| Рис. 3.12 |
Дата добавления: 2015-08-21; просмотров: 1086;
