При растяжении (сжатии)

Для определения опасных напряжений s₀ необходимо провести испытания образцов материала на растяжение и сжатие.

Растяжение образцов осуществляется на специальных испытательных машинах и сопровождается регистрацией усилий и соответствующих им деформаций. Большинство машин снабжено устройством, записывающим зависимость удлинения образца от приложенной к нему нагрузки. Вычерченная кривая в координатах F–Dl называется машинной диаграммой растяжения образца.

Для получения количественных оценок свойств материала диаграмма

F – Dl перестраивается в условную диаграмму s – e делением усилия F на первоначальную (до растяжения) площадь поперечного сечения образца A₀и удлинения рабочей части образца Dl на его начальную длину l₀.

В результате действия нагрузки длина стержня увеличится на величину , которая называется абсолютной продольной деформацией, или удлинением стержня (рис. 2.3).

Относительной линейной деформацией называется отношение абсолютной продольной деформации к начальной длине стержня:

(2.4) где 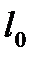– длина стержня до приложения нагрузки;

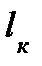– длина стержня после приложения нагрузки.

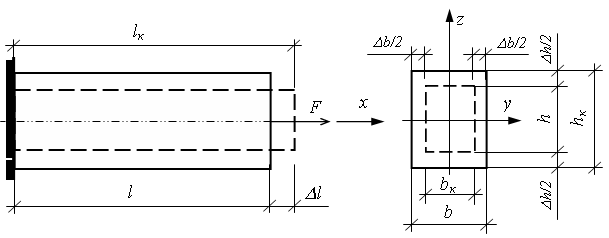
Рис. 2.3

Кроме продольной деформации стержень испытывает и поперечные деформации, которые определяются по формулам:

где – абсолютные поперечные деформации;

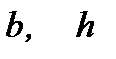– соответственно ширина и высота сечения до приложения к стерж-

ню нагрузки;

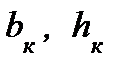– соответственно ширина и высота сечения после приложения нагрузки.

Как показывают эксперименты, при работе стержня в зоне упругости между продольными и поперечными деформациями существует линейная зависимость:

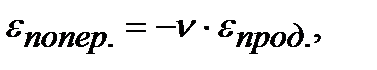или (2.5) где коэффициент Пуассона (безразмерная величина), зависит от материала

стержня ( 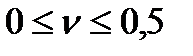) и является физической константой материала (для

стали n = 0,25…0,33; для бронзы – n = 0,32 … 0,35; для алюминия

n = 0,35 … 0,36; для пробки – n = 0; для резины – n =0,5).

Коэффициент Пуассона всегда положителен, а знак «минус» в формулах (2.5) указывает, что при растяжении стержня его поперечное сечение уменьшается и, наоборот, при сжатии – увеличивается.

На рис. 2.4 представлена типичная диаграмма s =f (e) для малоуглеро-дистой стали. Точками отмечены наиболее характерные моменты деформации материала.

Наибольшее напряжение, до которого справедлив закон Гука (точка а), называется пределом пропорциональности (s_пц).

Наибольшее напряжение, до которого материал не получает остаточные деформации (точка b), называется пределом упругости (s_у).

Предел текучести (s_т)– напряжение, при котором происходит рост деформации без заметного увеличения нагрузки (точка с).

Для материалов, не имеющих на диаграмме выраженной площадки текучести (участок bс), вводят понятие условного предела текучести s_0,2 – напряжения, при котором остаточная деформация равна 0,002, или 0,2 %.Опыты показывают, что разгрузка образца осуществляется всегда по закону Гука, т. е. параллельно участку Оа. При полной разгрузке, когда s = 0, упругие деформации снимаются и остаются только пластические. Следовательно, если на оси деформаций диаграммы s-e отложить от начала координат отрезок ОА, равный 0,002, и провести из точки А линию, параллельную прямой, выражающей закон Гука, то пересечение линии с диаграммой определит точку В, ордината которой будет соответствовать условному пределу текучести s_0,2 (рис. 2.5).

Временное сопротивление (s_в)– условное напряжение, которое соответствует наибольшему усилию в процессе растяжения образца (точка d на рис. 2.4):

.

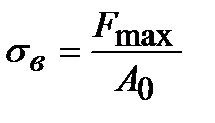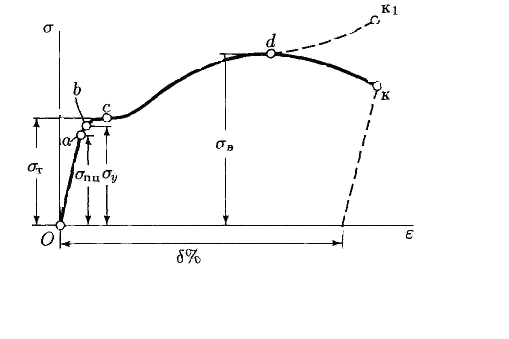
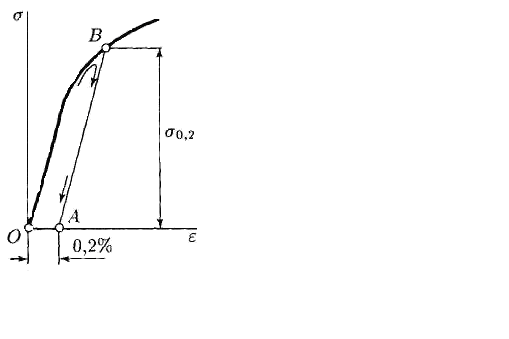
Рис. 2.4Рис. 2.5

До точки d деформация равномерно распределяется по длине образца, площадь поперечного сечения образца уменьшается, но не зависит от координаты сечения. Дальнейшее растяжение сопровождается локализацией пластических деформаций, что ведет к образованию шейки (рис. 2.6). Площадь поперечного сечения в зоне локализации пластической деформации резко уменьшается, что ведет к росту истинных напряжений, несмотря на снижение нагрузки (рис. 2.4, участок dк₁).

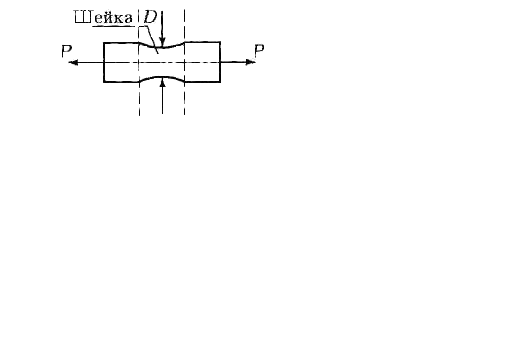
Рис. 2.6

Отношение растягивающего усилия в момент разрушения (F_к) к площади поперечного сечения в месте разрушения (А_к) характеризует истинное сопротивление разрушению (S_K):

.

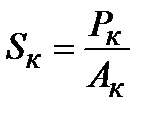Для цилиндрического образца А_K определяется путем замера диаметра в сечении, где произошло разрушение:

.

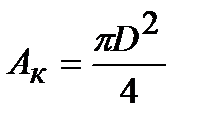Рассмотренные выше напряжения количественно характеризуют прочностные свойства материала.

Для характеристики пластических свойств материала определяют относительное удлинение образца после разрыва (d) и относительное сужение после разрыва (y).

Первая характеристика определяется отношением:

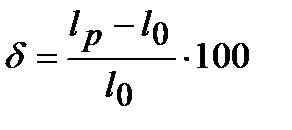%, (2.6)

где l_Р – длина рабочей части образца после разрушения.

Вторая характеристика определяется отношением:

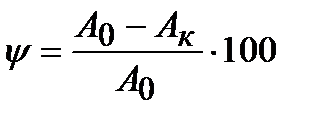%. (2.7)

Чем выше значения d и y, тем пластичнее материал. Обычно материал считается пластичным, если d > 5 %. Как правило, yнесколько выше значений d.

Противоположным свойству пластичности является хрупкость, т. е. способность материала разрушаться без образования существенных остаточных деформаций. Для хрупких материалов dне превышает 2…5 %.

Типичная диаграмма растяжения хрупкого материала показана на рис. 2.7. Она не имеет площадки текучести, и разрушение образца происходит практически без остаточных деформаций. Единственной характеристикой прочностных свойств материала в этом случае является предел прочности s_в.

Испытания на сжатие пластичных материалов свидетельствуют о том, что пределы пропорциональности, упругости и текучести, как правило, мало отличаются от аналогичных характеристик, полученных при растяжении.

Если необходимо отличить предел текучести при растяжении от предела текучести при сжатии, используют дополнительный индекс р для растяжения или с для сжатия. Таким образом, получаем обозначения s_тр и s_тс.

При испытаниях на сжатие пластичного материала невозможно осуществить разрушение образца. Цилиндрический образец получает бочкообразную форму, площадь поперечного сечения образца резко увеличивается (рис. 2.8). Это делает невозможным определение временного сопротивления при сжатии.

F

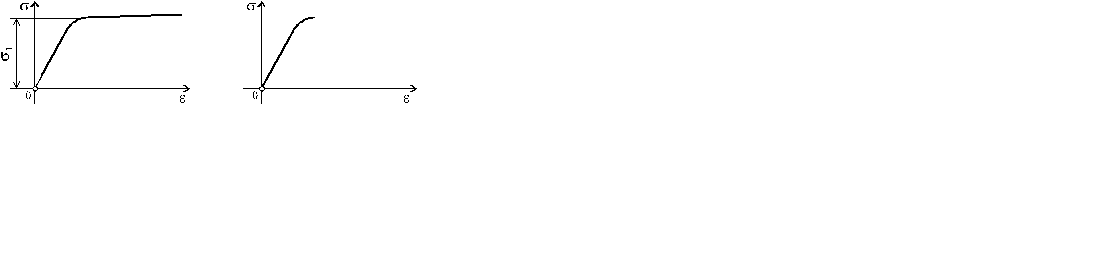
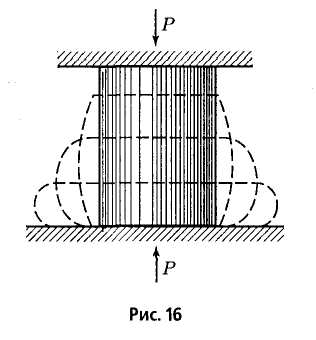
F

Рис. 2.7 Рис. 2.8

При сжатии хрупкого материала вид диаграмм s-e напоминает аналогичную диаграмму при растяжении. Однако, как правило, предел прочности при сжатии значительно выше, чем при растяжении. Характеристики, полученные при растяжении и сжатии, снабжаются дополнительным индексом р – для растяжения или с – для сжатия, например, при растяжении – s_вр, при сжатии – s_вс. Согласно одной из гипотез механики деформируемого твердого тела, между напряжениями и деформациями существует линейная зависимость (закон Гука, 1676 г.):

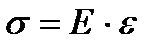, (2.8)

где 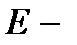модуль упругости первого рода (модуль Юнга) – механическая харак-

теристика материала.

Если заменить в формуле (2.8) выражения s и e, то можно получить другую форму записи закона Гука:

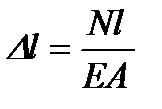, . (2.9)

Величина ЕА называется жесткостью стержня при растяжении (сжатии).