Напряжения при растяжении и сжатии

При растяжении и сжатии в сечении действует только нормаль­ное напряжение.

Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.

Таким образом, направление и знак напряжения в сечении со­впадают с направлением и знаком силы в сечении .

Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. По­этому напряжение можно рассчитать по формуле

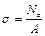рис.4.11

где N_z —продольная сила в сечении; А — площадь поперечного сечения. Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.

Нормальные напряжения действуют при растяжении от сечения (рис. 4.11, а), а при сжатии к сечению (рис. 4.11, б)

Размерность (единица измерения) напряжений — Н/м² (Па), од­нако это слишком малая единица, и практически напряжения рас­считывают в Н/мм² (МПа): 1 МПа = 10⁶ Па = 1 Н/мм².

При определении напряже­ний брус разбивают на участки (напряжений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.

Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.

Строится и оформляется такая эпюра так же, как и эпюра про­дольных сил.

Рассмотрим брус, нагру­женный внешними силами вдоль оси (рис. 4.12).

Обнаруживаем три уча­стка нагружения и определя­ем величины продольных сил.

Участок 1: N₁ = 0. Внутренние продольные силы равны нулю.

Участок2: N₂ = 2F. Про­дольная сила на участке поло­жительна.

Участок 3: N₃ = 2F—3F = —F. Продольная сила на участке отрицательна.

Брус — ступенчатый.

С учетом изменений ве­личин площади поперечного сечения участков напряжений больше.

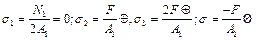рис.4.12

Строим эпюры продольных сили нормальных напряжений.

Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.