Центральное растяжение прямого бруса. Напряжения

Центральным растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечения бруса возникает только продольная (нормаль­ная) сила N, а все остальные внутренние силовые фак­торы равны нулю.

Явление центрального растяжения (сжатия) возника­ет только тогда, когда все внешние нагрузки действуют, по оси, проходящей через центры тяжести поперечных сечений бруса. Например, центральное растяжение испы­тывает трос башенного крана от веса поднимаемого гру­за. Условимся внутреннюю силу N считать положитель­ной, если она направлена от сечения (соответствует рас­тяжению), и отрицательной, если она направлена к сечению (соответствует сжатию).

В тех случаях, когда направление силы N неизвестно, следует ее принимать всегда положительной, т. е. растя­гивающей. Если после решения уравнения сила N полу­чится со знаком плюс, то брус в данном сечении будет растянут, если же со знаком минус, то сжат.

рис.4.10

Расчет начинается со свободного конца бруса, чтобы не определять величины реакций в опорах.

Рассмотрим прямой брус (рис. 4.10, а) постоянного и симметричного поперечного сечения, жестко закреплен­ный вверху и нагруженный тремя внешними сосредото­ченными силами F₁ = 10 кН, F₂ = 20 кН, F₂=30 кН, приложенными в точках В, С, D и направленными вдоль его продольной оси. Естественно, что на разных участках длины бруса будут возникать разные по величине вну­тренние продольные силы. В данной задаче таких участ­ков будет три: участок ВС, участок CD и участок DK.

Для нахождения внутренних продольных сил N вос­пользуемся методом сечений, т. е. мысленно рассечем брус плоскостью, перпендикулярной к его оси, на две ча­сти.

Поскольку к брусу приложены три внешние силы, то необходимо рассечь брус в трех местах, т. е. в пределах всех трех участков ВС, CD и DK, отбросить одну из час­тей и ее влияние на оставленную часть заменить неизве­стной пока внутренней силой N. Из условия равновесия 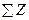=0 для оставленной части найти ее величину и направление. Приступим к решению нашей задачи.

Сечение 1—1. Рассекаем брус сечением 1—1 на две части, отбрасываем одну из них, например, верхнюю. Для упрощения расчета следует отбрасывать ту часть, на которую действует большее число внешних сил. В данном случае на верхнюю часть действуют три силы, поэтому целесообразнее ее отбросить, а оставить ниж­нюю часть, на которую действует только одна сила F₁. Заменяем действие отброшенной части неизвестной про­дольной силой N₁ предполагая последнюю растягиваю­щей, получим схему (рис. 4.10,б).

Составляем условия равновесия для оставленной ча­сти бруса: 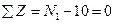, откуда 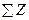==10 кН. Отсюда видно, что сила N₁ постоянна на всем протяжении уча­стка ВС, так как независимая переменная zне вошла в уравнение равновесия.

Сечение 2—2. Для определения продольной силы N₂ в произвольном сечении 2—2 поступаем совершенно ана­логично предыдущему (рис. 4.10,в). Составляем урав­нение равновесия: 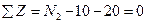, N₂=30 кН.

Сечение 3—3. Для определения продольной силы ЛГ₃ в сечении 3—3 рациональнее было бы оставить верхнюю часть, но при этом надо было предварительно определить реакцию R_K в жесткой опоре. Так как мы ее не находи­ли, оставим нижнюю часть (рис. 4.10, г), для которой уравнение равновесия запишется в виде 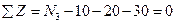, откуда N₃ = 60 кН.

Для наглядного представления характера (закона) изменения какого-либо из внутренних силовых факторов длине бруса строят график изменения этого фактора, в котором абсцисса соответствует местоположению сече­ния на оси, а ордината показывает значение исследуе­мого фактора в данном сечении. Такой график называ­ется эпюрой. Перейдем к построению эпюры продольных сил для заданного бруса. В данном случае брус содер­жит три участка, поэтому для построения эпюры N необ­ходимо провести исследование изменения продольной силы на каждом участке отдельно.

На участке ВС из уравнения равновесия мы опреде­лили величину N₁ = 10 кН и установили, что ее значе­ние в пределах этого участка не меняется, т. е. всюду остается постоянной N₁ = 10 кН, где бы мы ни прово­дили сечение 1—1. Следовательно, график продольной силы N₁ на первом участке будет постоянным.

На участке DC закон изменения продольной силы N₂ тоже будет постоянным в силу того, что переменная z не входила в уравнение равновесия. График на этом уча­стке отличается от графика на первом участке только величиной, так как N₂ = 30 кН.

На участке DK закон изменения продольной силы N₃ также будет постоянным (N₃=60 кН).

Эпюрой силы называется график распределения продольной силы вдоль оси бруса.

Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные —вверх, отрицательные —вниз.

В пределах одного участка значение силы не меняется, поэто­му эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.

На эпюре проставляются значения N_z. Величины продольных сил откладывают в заранее выбранном масштабе.

Эпюра по контуру обводится толстой линией и заштриховыва­ется поперек оси.

Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.

Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.

Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.

Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.