Способ замены плоскостей проекций

Условия преобразования:

1) положение фигуры неизменно;

2) изменяется положение одной из двух плоскостей проекций;

3) новую плоскость проекций располагают перпендикулярно оставшейся плоскости проекций (рис 1).

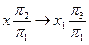
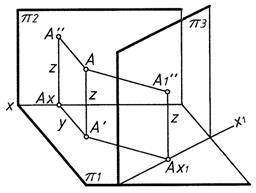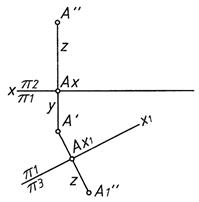Рис. 1

4) Положение новой плоскости проекций может быть задано или выбрано.

Построение профильной проекции точки (фигуры) есть также использование способа замены плоскостей проекций (рис. 2)

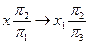
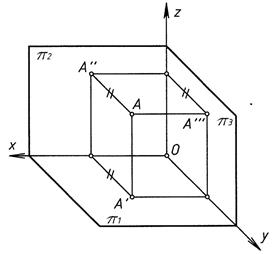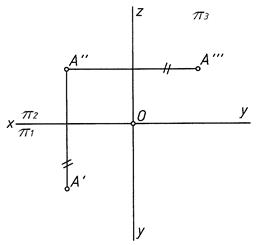Рис. 2

Метрические задачи, решаемые способом замены плоскостей проекций:

Примеры задач.

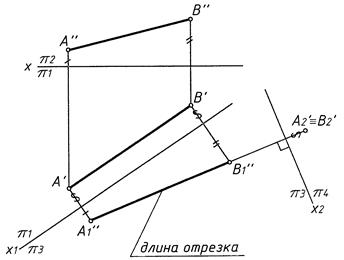
Задача 1. Определить длину отрезка (рис. 3)

Задача 2. Преобразовать прямую общего положения в проецирующую (см. рис. 3)

Первая замена

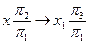
z = const

Вторая замена

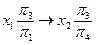
y = const

Рис. 3

Задача 3. Преобразовать плоскость общего положения в проецирующую.

Определить угол наклона плоскости к горизонтальной плоскости проекций (рис. 4).

Задача 4. . Преобразовать плоскость общего положения в плоскость уровня (см. рис. 4).

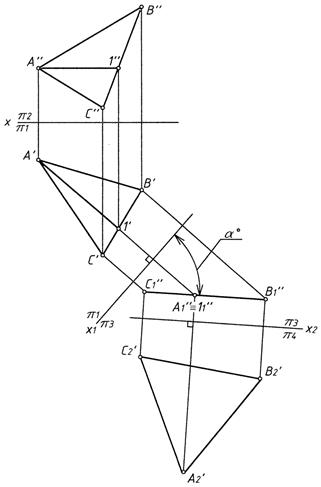Определить истинный вид плоскости ∆ ABC.

Рис. 4

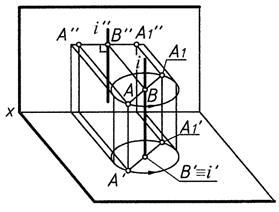
Способ вращения вокруг проецирующей прямой –частный случай плоско-параллельного перемещения.

Условия преобразования:

1) ось вращения i неподвижна и перпендикулярна плоскости проекций;

2) все точки фигуры перемещаются по окружностям, плоскости которых перпендикулярны оси i (рис.5);

3) точки лежащие на оси вращения i неподвижны (см. рис. 5)

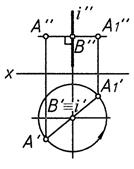Рис. 5

Пример задачи:

Определить длину отрезка вращением вокруг проецирующей прямой (рис. 6)

Рис. 6