Принципы обнаружения и исправления ошибок в принятой кодовой комбинации циклического кода

Переданная кодовая комбинация двоичного циклического кода, представленная полиномом F(x), из-за искажений единичных элементов в каналах связи может быть принята с ошибками и иметь вид некоторого полинома Н(х). Если просуммировать по mod2 одноименные разряды F(х) и Н(х), то получим

F(х) 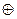Н(х)=Е(х),

где Е(х) – полином ошибок.

Разрядность полинома ошибок такая же, как и разрядность комбинации F(х) циклического кода. При этом ненулевые разряды в Е(х) указывают на ошибочные элементы в принятой кодовой комбинации Н(х). При отсутствии ошибок полином Е(х) состоит из одних нулей.

Принимая во внимание вышеприведенные обозначения, принятую кодовую комбинацию можно представить следующим образом:

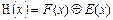
Для обнаружения ошибок в принятой кодовой комбинации Н(х) следует разделить Н(х) на порождающий многочлен Р(х). Результат деления укажет на наличие или отсутствие ошибки в принятой кодовой комбинации Н(х). Если деление дает нулевой остаток, то ошибки отсутствуют или не обнаружены. Если же в результате деления полинома Н(х) на порождающий многочлен Р(х) остаток R^’(х) отличен от нуля , то это означает что принятая кодовая комбинация Н(х) содержит ошибки (рис 2).

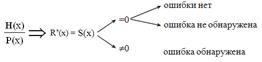
Рис.2. Схема выявления ошибок в принятой кодовой комбинации H(x)

Вид ненулевого остатка R’(x), называемого синдромом ошибки S(х), имеет однозначное соответствие с ошибочным разрядом и видом полинома однократной ошибки Е(х) для всех кодовых комбинаций Н(х) циклического кода. Например, для циклического кода (9,5) при заданном порождающем многочлене P(x)= x⁴ + x + 1 остаток R’(x) всегда будет иметь вид S(х)=0011, если ошибка возникла в пятом разряде входной кодовой комбинации, т.е. в младшем информационном разряде, независимо от вида переданной кодовой комбинации F(х).

Следует отметить, что остаток R’(x), получаемый при делении полинома Н(х), на порождающий многочлен Р(х), имеет такой же вид, как и остаток от деления Е(х) на Р(х), поскольку полином F(х) делится на Р(х) без остатка.

Кратность обнаруживаемых ошибок в принятой кодовой комбинации циклического кода определяется минимальным кодовым расстоянием d_min этого кода. Для циклического кода (9,5) значение d_min=3, что обеспечивает гарантированное обнаружение всех однократных и двукратных ошибок. Кроме того, код позволяет обнаруживать часть ошибок более высокой кратности, начиная с веса, равного d_min и более. Код не обнаруживает ошибки, если полином ошибки имеет вид разрешенной кодовой комбинации.

Для исправления однократной ошибки в принятой кодовой комбинации Н(х) необходимо определить место ошибки. С этой целью также производится деление полинома Н(х) на порождающий многочлен Р(х). Для определенности вновь обратимся к коду (9,5). Если на 9^ом такта в регистре-делителе (декодирующем регистре) будет зафиксирована хотя бы одна единица, то деление продолжается до тех пор, пока в регистре-делителе не будет зафиксирована “особая” кодовая комбинация. Вид этой комбинации зависит только от вида порождающего многочлена Р(х) и длины n комбинации циклического кода F(х), причем находится “особая” кодовая комбинация как остаток от деления хⁿ на P(x) [3]. В нашем случае, для кода (9,5) и порождающего многочлена Р(х)=х⁴+х+1 “особая” кодовая комбинация, всегда имеет вид 1010.

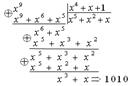
Номер такта, на котором в регистре-делителе возникает “особая” кодовая комбинация, указывает место ошибочного разряда в принятой кодовой комбинации Н(х). При считывании этой комбинации из буферного регистра ошибочный разряд должен быть исправлен (инвертирован).

Циклический код (9,5) гарантированно исправляет только однократные ошибки. Ошибки более высокой кратности код (9,5) не исправляет.

Заметим также, что деление полинома Н(х) на многочлен Р(х) и считывание информации из буферного регистра после 9^го такта целесообразно осуществлять под действием “быстрых” тактовых импульсов. Это позволит без задержки принять из канала связи и обработать следующую кодовую комбинацию Н(х).

1. Структурная схема кодирующего и декодирующего устройства ( циклич. Коды ).