Модель оценки стоимости активов

Инвесторы сталкиваются с проблемой оценки стоимости активов. Она зависит главным образом от их риска и доходности. На рынке выдерживается закономерность: чем выше потенциальный риск, тем выше должна быть и ожидаемая доходность. У каждого инвестора формируются свои прогнозы относительно отмеченных параметров. В то же время рынок постоянно движется в направлении определенной равновесной оценки риска и доходности активов. Возможные расхождения в оценках, в первую очередь, связаны с ассиметричностью информации, которой обладают разные инвесторы. В условиях хорошо развитого рынка новая информация находит быстрое отражение в курсовой стоимости активов. Поэтому для таких условий можно разработать модель, которая бы удовлетворительно описывала взаимосвязь между риском и ожидаемой доходностью активов. Такая модель разработана в середине 60-х гг. У. Шарпом и Дж. Линтерном и получила название модели оценки стоимости активов(capital asset pricing model — САРМ). Как известно, стоимость актива определяется путем дисконтирования будущих доходов, которые он принесет, под процентную ставку, соответствующую его риску. Модель оценки стоимости активов не дает непосредственного ответа на вопрос, какой должна быть цена актива. Однако она получила такое название, потому что позволяет определить ставку дисконтирования, используемую для расчета стоимости финансового инструмента. В модели устанавливаются следующие ограничения: рынок является эффективным, т. е. в курсовой стоимости актива новая информация сразу находит отражение1, активы ликвидны и делимы, отсутствуют налоги, транзакционные издержки, банкротства, все инвесторы имеют одинаковые ожидания, действуют рационально, стремясь максимизировать свою полезность, имеют возможность брать кредит и предоставлять средства под ставку без риска, рассматривается один временной период, доходность является только функцией риска, изменения цен активов не зависят от существовавших в прошлом уровней цен.

Рис. 4 Линия рынка капитала.

В CAPM зависимость между риском и ожидаемой доходностью графически можно описать с помощью линии рынка капитала (Capital Market Line – CML), которая представлена на рис. 4. М – это рыночный портфель; 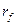- актив без риска; 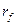L – линия рынка капитала, 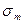- риск рыночного портфеля; E( 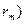- ожидаемая доходность рыночного портфеля.

Все возможные оптимальные (эффективные) портфели, т.е. портфели , которые включают в себя рыночный портфель М, расположены на линии 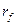L.

CML поднимается вверх слева направо и говорит о том, что если портфель имеет более высокий риск, то он должен предлагать инвестору и более высокую доходность, и если вкладчик желает получить более высокую ожидаемую доходность, то он должен быть согласен и на более высокий риск.

Когда вкладчик приобретает актив без риска, он обеспечивает себе доходность на уровне ставки без риска.

CML представляет собой прямую линию. Уравнение данной линии можно представить следующим образом:

y = a + bx [31]

где а – значение ординаты в точке пересечения ее линией CML; оно соответствует ставе доходности 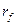; в – угол наклона CML.

Угол наклона определяется как отношение изменения значения функции к изменению аргумента. В нашем случае угол наклона равен:

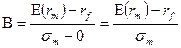
В принятых терминах риска и доходности уравнение CML примет вид:

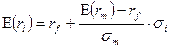[32]

где: 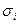- риск итого портфеля, для которого определяется уровень ожидаемой доходности; 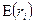- ожидаемая доходность итого портфеля.

Данное уравнение можно записать следующим образом:

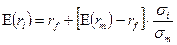[33]

Таким образом, ожидаемая доходность портфеля равна ставке без риска плюс произведение отношения риска портфеля к риску рыночного портфеля и разности между ожидаемой доходностью рыночного портфеля и ставкой без риска.