Метод отраженных волн

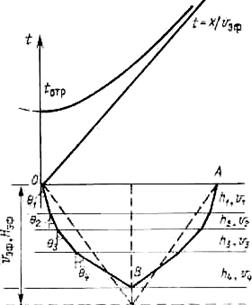
Прямые кинематические задачи метода отраженных волн при общем пункте возбуждения (ОПВ). Простейшей является задача о годографе для плоскопараллельно- го слоя. Выберем систему координат так, чтобы плоскость OXY совпадала с поверхно- стью земли, ось ОХ была направлена вдоль профиля, а ось OZ — вниз. Обозначим ско- рость продольных волн в слое и подстилающем полупространстве v1 и v2 соответствен- но, а мощность слоя — h (рис. 1.19). Расположим точечный источник возбуждения в начале координат, приемник—на расстоянии х от источника. Найдем время прихода отраженной от подошвы слоя волны в точку расположения приемника.

Согласно закону Снеллиуса, уголы OBA1 и A1BA равны, т.е. треугольник ОВА равнобедренный, так как нормаль к границе в точке В совпадает с направлением верти- кали. Следовательно, А1А=ОА1 и длина пути ОВА

l =2

(1.23)

Время пробега волны по этому пути

t( x )=1

v

(1.24)

Как следует из выражения (1.24), годограф отраженной волны в рассматриваемом

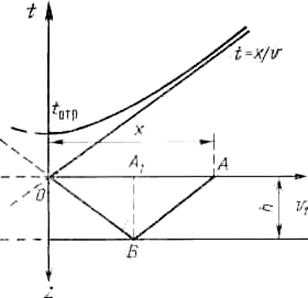
Рис.1.19 Годограф отраженной волны для горизонтальной отражающей границы.

tотр — годограф отраженной волны;

t=x/v — годограф прямой волны.

ны для слоистой среды

sinq2 =

vsinq1 ;

v1

sinq3 =

vsinq2 ;

v2

sinq4 =

vsinq3

Последовательно выражая sin θ2, sin θ3, sin θ4 через sin θ1, получаем

sinq1 =sinq2 =sinq3 =sinq4

v1 v2

v3 v4

В силу симметрии задачи относительно вертикальной оси ясно, что tn(x) — четная функция, т. е. t(x)=t(-х).

При небольших удалениях приемника от источника t(x) можно аппроксимировать зависимостью t2(x) = t0n2(x)+x2/v2эф или

2

t( x ) =

+x =

1

vэф

эф

(1.25)

где

t0 n

i =1 vi

(1.26)

Но уравнение (1.25) полностью совпадает с годографом (1.24) для однородного слоя с мощностью Нэф и скоростью vэф. Величина vэф простым образом связана с мощ- ностями и пластовыми скоростями реальной толщи:

vэф =

n

i =1

v2 ×Dti,

tn

Dti

=hi,

vi

n

tn =å Dti

i =1

(1.27)

равна сумме взвешенных квадратов пластовых

скоростей. Весовые множители

Dti

t n придают большую значимость тем скоростям,

которые вносят больший вклад в общее время пробега.

Для выяснения смысла Hэф и vэф рассмотрим величину средней скорости vср в слоистой пачке. Как следует из выражения (1.24), при х=0 по годографу отраженной волны можно определить двойное время пробега волны по нормали от источника к соответствующей границе и обратно

t0 n =2

=2 Н эф

(1.28)

i =1 vi

vэф

Средняя скорость распространения волны в этом направлении

vср =

h1+h2 +"+h n

h1 v1 +h2 v2 +"+hn vn

n

=åvi

i =1

Dt i

t0 n

(1.29)

Сравнивая выражения (1.27) и (1.29) можно заключить, что vэф>vср и стремится к vcp, когда скорости в пластах мало отлича- ются друг от друга. Мощность эффективного слоя Hэф согласно выражению (1.28)

H эф =

1

vэф ×

t0 =

H ×vэф

vср

(1.30)

Рис.1.21 Годограф отраженной волны для наклонной отражающей границы:

О* — положение мнимого источника;

tmin — минимальное время

Но, поскольку vэф.>vср, Нэф>Н — ис-

тинной глубины до отражающей границы.

Таким образом, эффективный слой — это однородный слой с мощностью и скоро- стью, превышающими истинную мощность слоистой толщи и среднюю скорость в ней.

Найдем теперь годограф отраженной волны для слоя с наклонной подошвой (рис.1.21). Скорость волн в слое обозначим v1, а профиль проведем вкрест простирания его подошвы. Точечный источник снова рас- положим в начале координат так, чтобы ось OZ была направлена вниз, а ось ОХ совме- щена с профилем. Рассмотрим луч падающей волны, составляющий угол θ с осью OZ. То- гда угол падения луча на границу будет θ+φ, где φ — угол наклона границы. Проведем из точки О нормаль к границе и отложим на ней

отрезок 2OB. Треугольники ОВР и 0*ВР прямоугольные и конгруэнтные. Следова-

тельно, ОР=О*Р и угол O*PO=180°—2(θ+φ), а угол OPA=2(θ+φ).

Угол 0*РА является суммой вычисленных углов O*PA=180°, а точки О*, Р, А лежат на одной прямой, путь 0*Р+РА=0*А. Кинематика волн оказывается такой, ка- кой она была бы, если вместо реального источника, расположенного в точке О, рас- сматривать безграничную среду со скоростью v1, в которой источник расположен в точке О*. Такой источник называют мнимым. Его использование часто значительно упрощает решение кинематических задач. При использовании мнимого источника на- ходим путь

O * A =

(O * D)2 +(DA)2

Но OD = О*0·sin φ=2OB sin φ, 0*D= =2OB cos φ, AD=x+OD. Остается выра- зить ВО через истинное значение глубины z0 до отражающей границы под источником, полученной по данным бурения: Z0=BO/cos φ.

В действительности целесообразнее использовать не глубину по вертикали, а ми- нимальное расстояние от источника до границы OB — эхоглубину h, и при известной скорости v1 ее можно получить, если приемник будет расположен в непосредственной близости от источника. Имея в виду, что BO = h, окончательно находим

O * A =

t( x) =1

v

4h2 ×cos2 j+( x ±2h ×sinj)2 =

x2 ± 4hx × sin j + 4h2

x 2 ± 4hx × sin j + 4h2

(1.31)

Поскольку второе слагаемое в формуле есть квадрат действительной величины,

t(x) достигает минимального значения, когда

x ±2h ×sin j=0 т. е.

xmin

= #2h × sin j ,

tmin

=2h cosj=t

v 0

cosj ,

t =2h

0 v

(1.32)

Как видно из выражений (1.31), t(x) — это гипербола, но ее минимум смещен вдоль профиля по восстанию границы на расстояние 2h·sin φ. Это смещение называют сейсмическим сносом.

Использование эффективных скорости и мощности позволяет годограф волны,

отраженной от границы в толще, состоящей из наклонных пластов, представить в виде

t( x ) =

1

vэф

(1.33)

где Hэф — эффективная эхоглубина под пунктом возбуждения;

vэф — эффективная скорость; φ — угол наклона пластов.