Практичні рекомендації з визначення кристалографічних символів

1. Символи одиничної грані, якщо вона перетинає всі три координатні осі (111), незалежно від того, які відрізки – рівні чи нерівні відтинає вона по цих осях. В цьому легко переконатися, підставивши в загальну формулу замість, А_x, В_x, С_x – ОА₁, ОВ₁ ,ОС_1.

Доказ: 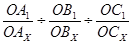= =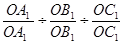1 .

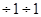Якщо грань, в тому числі одинична, паралельна одній або двом координатним осям, то індекс, що відповідає даним осям, дорівнює нулю. Нехай грань паралельна осям Х та Y, тобто ОА_x = 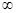, то ОВ_x = 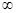, тоді:

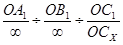=0 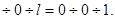Індекс грані (001).

3. Для визначення символу грані кристала кубічної сингонії достатньо замірити її параметри по трьох осях ( в см, мм) та взяти зворотні величини, тому що ОА₁ = ОВ₁ = ОС₁, тоді:

= = .

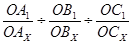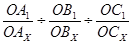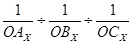4. В тетрагональній сингонії ОА₁= ОВ₁ 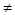ОС₁, тому загальна формула приймає вигляд: .

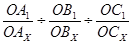У випадку вертикальних граней, тобто при ОС_х = ,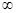

=

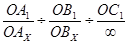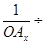
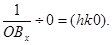
5. В триклинній, моноклинній та ромбічній сингоніяхчасто реальна одинична грань, що перетинає всі три координатні осі, відсутня. У вказаних сингоніях частіше всього використовуються індекси 1, 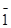,0 (рис. 3.4).

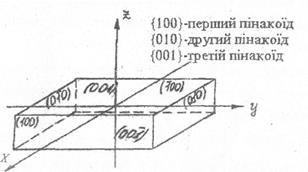
Рис. 3.4.Символи граней і простих форм прямокутного паралелепіпеда (ромбічна сингонія)

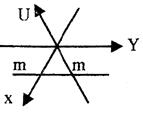
6. За одиничну грань в тригональних та гексагональних кристалах приймають таку грань, яка відтинає рівні відрізки на двох горизонтальних осях та нерівній по осі Z.

Можливі два випадки:

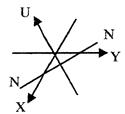
І) грань, що відсікає рівні відрізки на двох сусідніх осях, утворюючих одна з другою кут 60°, проходить паралельно третій:

ММ(10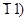

2) грань, що відсікає рівні відрізки на двох горизонтальних осях, утворюючих кут 120°, перетинає третю вісь. Відрізок на останній осі вдвічі коротший відрізків по двох інших осях.

NN(1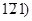

Важливо помітити, що алгебраїчна сума перших трьох індексів завжди дорівнює нулю. З чотирьох індексів грані hkil третій і не є незалежним і визначається першими двома: і = -(h +k).

Для прикладу позначення граней кристалів за допомогою символів повернемося до рис. 3.1. Відповідно правила установки (табл. 3.1) вісь Z вибираємо вздовж L₄. Осі X, Y у випадку: а) – по осях L ₂, що проходять через середини ребер кристалу; у випадку б) – по осям L ₂, що проходять через середини граней; тоді одинична грань дипіраміди і в тому, і в другому випадках відтинає на двох горизонтальних осях рівні масштабні відрізки та нерівний відрізок на третій осі.

а) Символи граней дипіраміди:

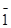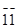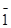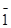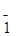
(111),( 11),( 1),(1 1),(1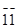1 ),( ),(1 ),( ).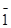

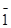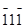Узагальнений символ простої форми {111}.

Символи граней призми:

(110), ( 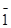10), ( 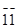О), (1 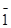0).

Узагальнений символ простої форми {110}.

б) Символи граней дипіраміди аналогічні а).

Символи граней призми:

(100), (01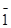0), ( 00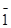), (0 0)

Узагальнений символ {100}.

Наведені символи дають чітке уявлення. про неоднакове розташування граней на обох кристалах.

Завдання. Користуючись поясненнями до роботи, для двох-трьох моделей кристалів дати повну характеристику їх зовнішній формі за такою схемою: